Leetcode word search (backtracking method)

subject

Given a  m x n Two dimensional character grid  board And a string word  word . If  word Exists in the grid , return true ; otherwise , return false .

The words must be in alphabetical order , It's made up of letters in adjacent cells , among “ adjacent ” Cells are those adjacent horizontally or vertically . Letters in the same cell are not allowed to be reused .

Example 1：

Input ：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output ：true
Example 2：

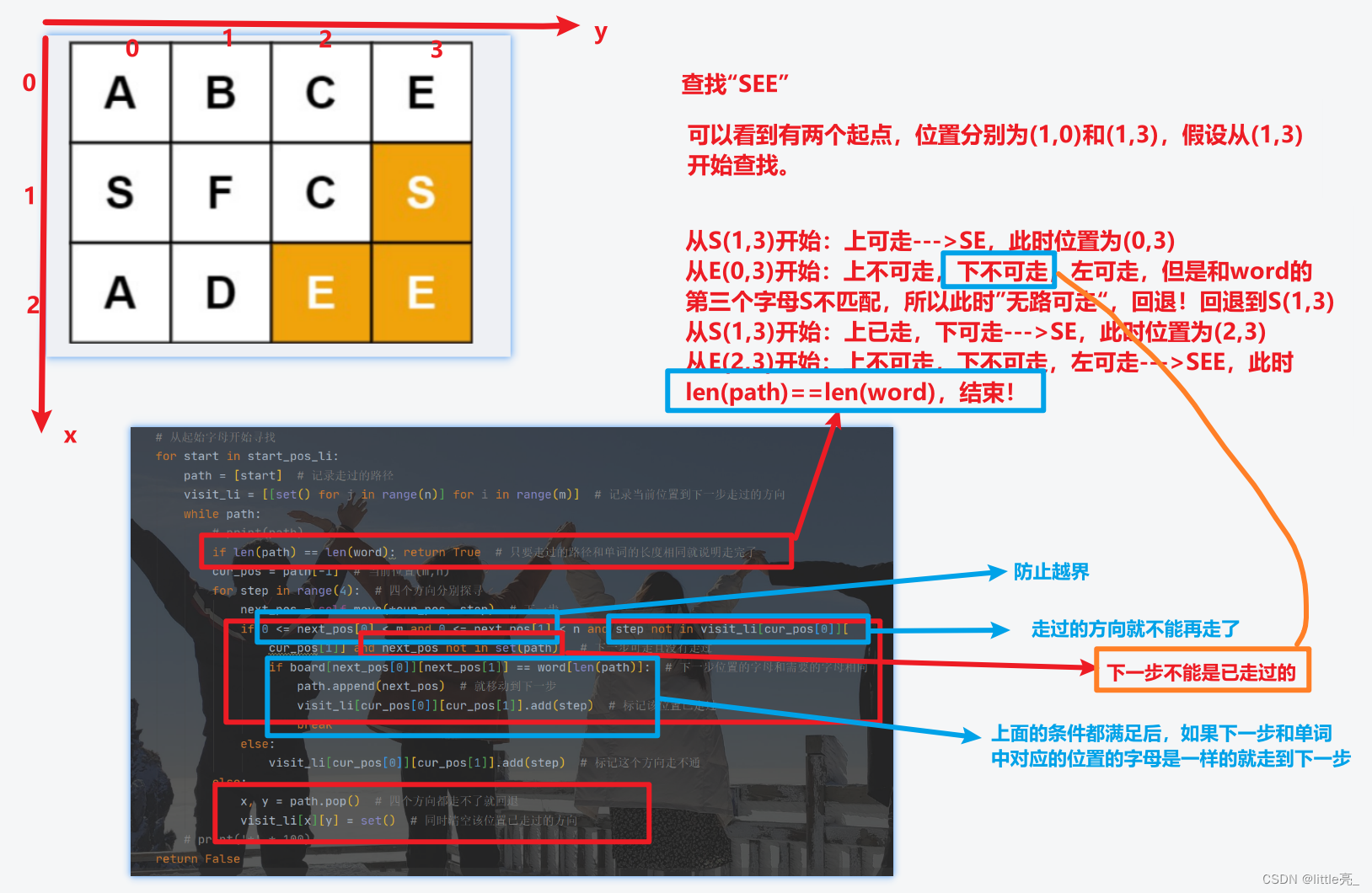
Input ：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output ：true
Example 3：

Input ：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output ：false
 

Tips ：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board and word It consists of upper and lower case English letters only

source ： Power button （LeetCode）
link ：https://leetcode.cn/problems/word-search
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .

Ideas

Because I just did a maze problem not long ago , So after reading this question , I found it amazingly similar to walking through a maze , It's just that the conditions change when we take the next step . however , It still cost me 2 How close are you to 3 It took hours to write ！, alas , Don't say the , It's still too much for me .

Get down to business （ Food can't be a reason for my laziness ）

First , Whether it's maze walking or this problem , There must be a starting point , For this question , If you try one by one , That would be too time-consuming , So I first traverse the whole grid ,  Find the position of the letter that is the same as the first letter of the word you want to find ：

 start_pos_li = []  #  Record the position of the first letter of the word 
        word_set = set()  #  All letters in the table 
        m, n = len(board), len(board[0])
        for i in range(m):
            for j in range(n):
                word_set.add(board[i][j])
                if board[i][j] == word[0]:
                    start_pos_li.append((i, j))

The found letters are added to start_pos_li In this list , Easy to find in the future, directly start from these locations .

At the same time, I also set up a set word_set, Save all the letters appearing in the grid , Before the official search , You can make a simple judgment to quickly get the answer of some chestnuts ：

        for s in word:
            if s not in word_set: return False  #  As long as there is a letter not in the table, it returns False

As the code shows , Traverse the words you need to find , As long as there is a letter not in the set, it will be returned directly False.

Now let's start the formal search

 1. First define a move rule ：

 #  Move ( Four directions )
    def move(self, x, y, direction):
        if direction == 1:
            return (x - 1, y)
        elif direction == 2:
            return (x + 1, y)
        elif direction == 3:
            return (x, y - 1)
        else:
            return (x, y + 1)

1 Represents moving up ,2 Represents moving down ,3 Represents shift left ,4 For shift right ; Here I take the horizontal axis as y Axis , Vertical axis as x Axis , therefore When moving up and down x Axis found changes , When moving left and right y The axis changes .

2. Begin to walk tentatively

a. Define a “ Stack ” To save the path

path = [start]  #  Record the path 

In fact, here is a list , But only using append() and pop() Method , Then it behaves like a stack .

b. Define a list to save the direction of each grid

visit_li = [[set() for j in range(n)] for i in range(m)]  #  Record the direction from the current position to the next step 

Here I use a set to store the direction of each grid , A grid can store up to four directions , That is, up and down, around ; Unlike going through a maze , In maze walking, it is represented by two values ：0 Represents that the current grid has not passed ,1 Represents that the current grid has left ; Because here is a word , It requires a continuous sequence , The current grid may not come from this direction , But you can come from the other direction .（ That is, take the grid from different directions , The sequences obtained are all different ）

c. Probe + to flash back

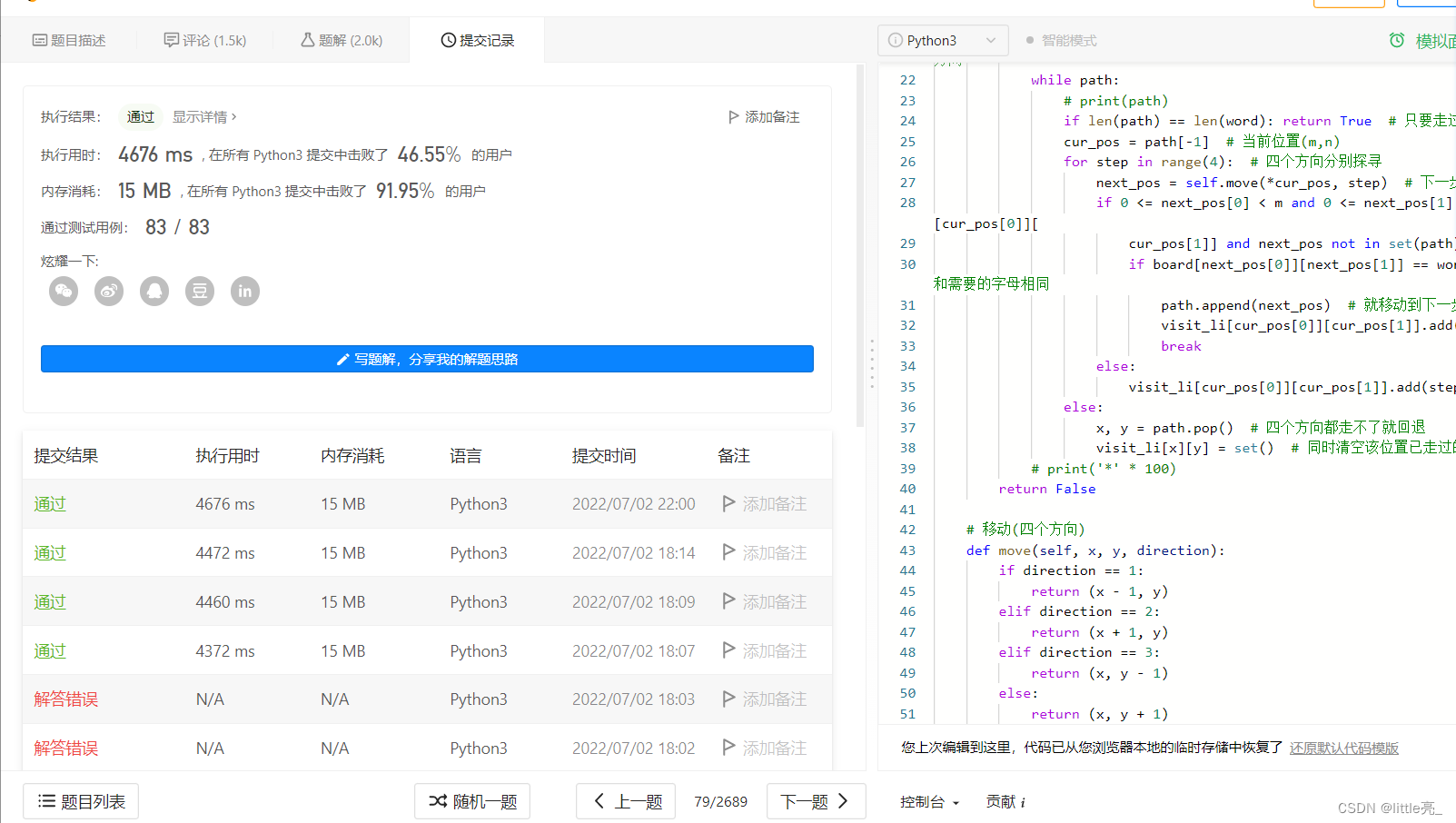
#  Start with the initial letter 
        for start in start_pos_li:
            path = [start]  #  Record the path 
            visit_li = [[set() for j in range(n)] for i in range(m)]  #  Record the direction from the current position to the next step 
            while path:
                # print(path)
                if len(path) == len(word): return True  #  As long as the path is the same as the length of the word, it means that you are finished 
                cur_pos = path[-1]  #  The current position (m,n)
                for step in range(4):  #  Explore in four directions 
                    next_pos = self.move(*cur_pos, step)  #  next step 
                    if 0 <= next_pos[0] < m and 0 <= next_pos[1] < n and step not in visit_li[cur_pos[0]][
                        cur_pos[1]] and next_pos not in set(path):  #  The next step can be taken without going through 
                        if board[next_pos[0]][next_pos[1]] == word[len(path)]:  #  The letters in the next position are the same as those required 
                            path.append(next_pos)  #  Just move to the next step 
                            visit_li[cur_pos[0]][cur_pos[1]].add(step)  #  Mark that the position has passed 
                            break
                    else:
                        visit_li[cur_pos[0]][cur_pos[1]].add(step)  #  Mark that this direction won't work 
                else:
                    x, y = path.pop()  #  If you can't walk in four directions, go back 
                    visit_li[x][y] = set()  #  At the same time, clear the direction that the position has passed 

From the beginning , Test whether the four directions can go in turn , If the walkable point is updated to the current position , And then continue to test , If to a certain point , None of the four directions will work , Then go back , Go back to the previous step ; Continue the direction you didn't finish last time , Take the following chestnut as an example ：

Source code

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        '''
         It's like going through a maze , Set up 4 Two directions of movement , At the same time, mark the places you have passed 
        '''

        start_pos_li = []  #  Record the position of the first letter of the word 
        word_set = set()  #  All letters in the table 
        m, n = len(board), len(board[0])
        for i in range(m):
            for j in range(n):
                word_set.add(board[i][j])
                if board[i][j] == word[0]:
                    start_pos_li.append((i, j))

        for s in word:
            if s not in word_set: return False  #  As long as there is a letter not in the table, it returns False

        #  Start with the initial letter 
        for start in start_pos_li:
            path = [start]  #  Record the path 
            visit_li = [[set() for j in range(n)] for i in range(m)]  #  Record the direction from the current position to the next step 
            while path:
                # print(path)
                if len(path) == len(word): return True  #  As long as the path is the same as the length of the word, it means that you are finished 
                cur_pos = path[-1]  #  The current position (m,n)
                for step in range(4):  #  Explore in four directions 
                    next_pos = self.move(*cur_pos, step)  #  next step 
                    if 0 <= next_pos[0] < m and 0 <= next_pos[1] < n and step not in visit_li[cur_pos[0]][
                        cur_pos[1]] and next_pos not in set(path):  #  The next step can be taken without going through 
                        if board[next_pos[0]][next_pos[1]] == word[len(path)]:  #  The letters in the next position are the same as those required 
                            path.append(next_pos)  #  Just move to the next step 
                            visit_li[cur_pos[0]][cur_pos[1]].add(step)  #  Mark that the position has passed 
                            break
                    else:
                        visit_li[cur_pos[0]][cur_pos[1]].add(step)  #  Mark that this direction won't work 
                else:
                    x, y = path.pop()  #  If you can't walk in four directions, go back 
                    visit_li[x][y] = set()  #  At the same time, clear the direction that the position has passed 
            # print('*' * 100)
        return False

    #  Move ( Four directions )
    def move(self, x, y, direction):
        if direction == 1:
            return (x - 1, y)
        elif direction == 2:
            return (x + 1, y)
        elif direction == 3:
            return (x, y - 1)
        else:
            return (x, y + 1)

Through screenshots

Synchronous update in personal blog system ：LeetCode Word search ( To solve by backtracking )