当前位置:网站首页>计组笔记(1)——校验码、原补码乘除计算、浮点数计算
计组笔记(1)——校验码、原补码乘除计算、浮点数计算
2022-07-05 04:34:00 【愿此后再无WA】
本篇知识点学习自B站 @王道论坛,支持正版。点此进入->王道计算机考研 计算机组成原理
写这篇笔记的最初目的是给自己看的,以后如果有些知识点忘了可以回顾一下。当然,大家想看也没有问题,但我比较建议大家看视频学习。
校验码
奇偶校验码
奇偶校验码,在N个有效信息位中添加一位校验位用于检测该数据在传输过程中是否出现错误。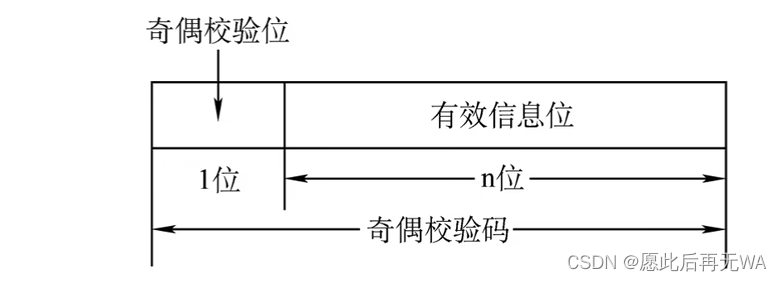 奇偶的定义是看整个校验码(校验位+信息位)中 1 出现的个数,若采用奇校验码,则校验码中 1 出现的个数为奇数,反之为偶数。
奇偶的定义是看整个校验码(校验位+信息位)中 1 出现的个数,若采用奇校验码,则校验码中 1 出现的个数为奇数,反之为偶数。
例:求编码 10110101 的奇偶校验码。
设最高位为校验位,那么我们可以先写成这样的形式:_10110101,其中_为待填的校验位,共有奇数个1(5个),为使校验码中有奇数个1,那么奇校验码的校验位应为0,即010110101,为校验码中有偶数个1,那么偶校验码的校验位应为1(此时共有6个1)。
根据上面的校验码我们可以知道,当其中有1个或奇数个位由0变为1或由1变为0时,可以检测出错误;但有偶数个位出现跳变时,该方法便无法检测异常。
奇偶校验码还有一个缺点就是,就算能检测出错误,也无法判断哪一位出了问题,只能要求对方重传数据。
注意这里只是对视频的部分知识点做一个总结,比较建议大家先看完视频再来看这篇。
为解决无法检测错误的问题,海明发现了一种能够进行错误检测的海明码。
海明码的大致思路是:将信息位分成k组,然后分别对每组进行偶校验,通过多个校验位标记出错位置并巧妙的修正。
那么需要多少位校验位呢?假设信息位有n位,校验位有k位,那么校验码共有n+k位,而一个校验码能表示两种状态,那k个校验码能表示2 ^ k种状态。一种状态能表示一个地方出错(这里只讲检测并修正一位的海明码),那么就有n+k个位置可能出现错误,此外还需要一个状态来表示正确的情况。结合上述说明,就出现了这么一条式子:2 ^ k >= n+k+1.(k表示校验位,n表示符号位)。结合例子讲解一下汉明码的求解步骤。
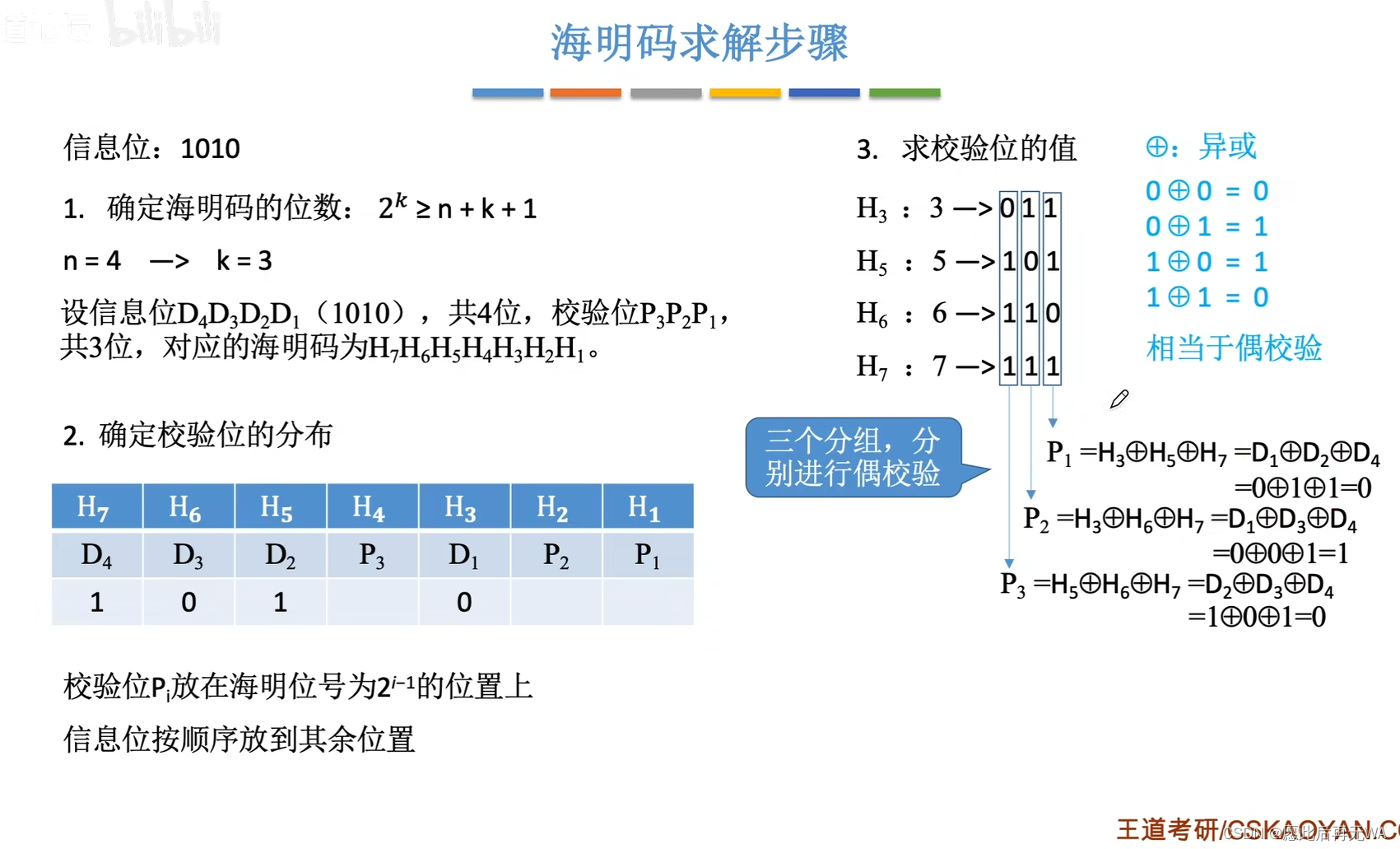
假设信息位为 1010.
- 根据式子 2^k >= n+k+1 确定校验位个数,因为信息位长度为4,即n=4,要使不等式成立,k的最小取值为3,即校验位长度为3.
- 标记元素区分状态。设信息位为D4,D3,D2,D1,校验位为P3,P2,P1,对应的海明码为H7H6H5H4H3H2H1.
- 确定校验位位置。校验位并不是随便都能放,Pi 必须放在 2^(i-1) 位置上,确定完校验位后,从左往右依次填入高位到低位的信息编码,注意顺序不能变。比如 1010,填入的时候也是按这个顺序,如果是1011,也是填入1011这个顺序,在每个信息位之间可能会有校验位,但信息位的相对位置不会变。 最后将信息位对应的值填入。

- 获取校验位的值。简单的说就是信息位所处的海明位的下标需要由几个2的 k次方 构成。就比如D1所处的海明码位置是H3,3=2+1,所以3由2的1次方加2的0次方构成,因此可以用H1和H2表示,即对应的p1,p2,同样的,5=4+1,所以H5可以用H4+H1来表示,即P3+P1…以此类推,可以知道每个信息位该如何表示出来,以及可以知道每个校验位能够表示哪些信息位。让每个校验位能够表示的信息位进行异或运算,即可得到校验位对应的值。
- 纠错。最后在得到的数据中,让校验位与他能够表示的信息位进行异或运算,如果得出的结果是0,则说明数据无误。如果出现一处错误,可以根据校验码之间的关系,总能够发现其中的错误出现位置。
 回顾一下,还记得如何求校验位的值吗?校验位的值就是用它所有能表示的信息位的值进行异或得出来的结果。
回顾一下,还记得如何求校验位的值吗?校验位的值就是用它所有能表示的信息位的值进行异或得出来的结果。
已经知道了信息位与校验位之间的联系,现在假设D4这个信息位出错,即由1跳变为0,看到图片上的第四点校验方程,并结合第二点的各个校验位分布可以得出,S1S2S3=111(从后往前数),而111由二进制转换成十进制是7,而H7对应的不就是D4的位置吗?是不是觉得很不可思议?我也就觉得,好好理解一下。
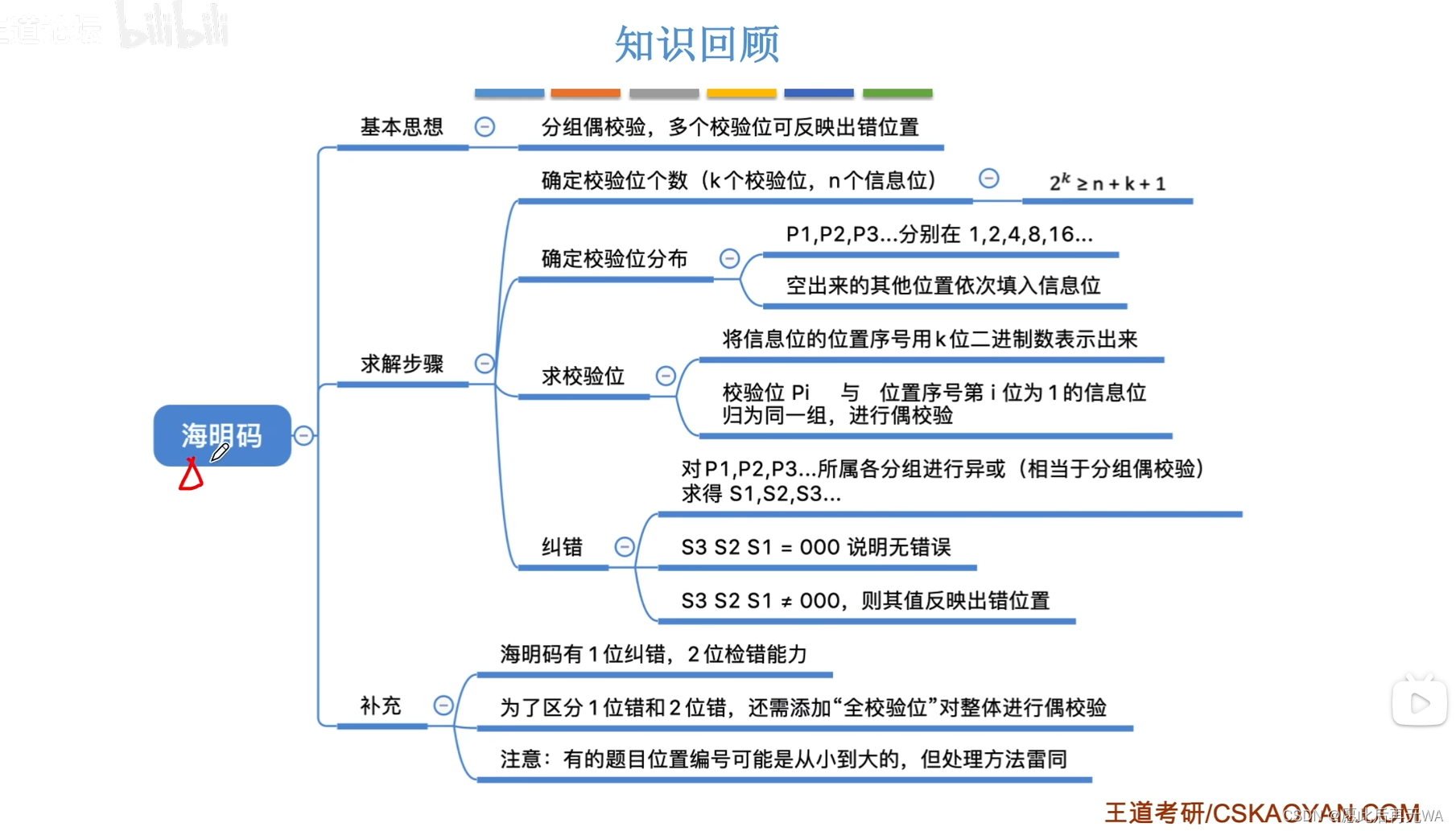
海明码具有 1 位纠错能力和 2 位检错能力。当校验码中同时出现两处跳变只能发现校验码中存在错误,而无法正确的判断出现错误的具体位置。还是以上图中的纠错方程为例,假设P1P2均发生跳变,那么S1S2S3得出的结果是011(从后往前数),如果按正常流程判断的话,就说明是H3这个位置出现错误,可并不是。
为了能正确识别出现两个数据发生跳变的情况,可以在校验码的基础上多添加个全校验位,它的值是此前校验码中所有值进行异或的结果,最后整体进行一次偶校验,并结合此前的纠错方程,便能得出是一位错误还是两位错误了,结合图示理解一下。
循环冗余校验码
还是建议先看视频再看总结。
简单的说,就是以传输的数据作为被除数,并且数据的发送方接收方约定一个多项式,根据多项式的系数来确定除数,以及根据多项式的最高项来确定需要在被除数后面添加几个0,最后将被除数与除数相除所得的余数与原有的0进行替换,那么这时候新生成的被除数与除数相除必定余数为0,若数据传输过程中,发生跳变,导致余数不为0,则说明数据有误,需要重传。
我们结合实例理解一下。
设生成多项式为G(x)=x3+x2+1,信息码为101001,求对应的CRC码。
- 确定除数。 多项式可以写成 1 · x3 + 1 · x2 + 0 · x1 + 1 · x0,然后把他们的系数拿出来,那么就是1101,而这个就是我们需要的除数了。
- 确定0的个数。我们需要知道在信息码后面补几个0。因为多项式的最高项是3,因此要在信息码后面补3个0,补上0后的信息码就是我们需要的被除数了。
- 求余数。我们让被除数与除数用模2除法、模2减法进行相除相减,得到余数。注意,余数可能是除不尽的,我们只需要除完3个0即可而无需继续在后面补0.
- 得到与多项式最高项相同长度的余数后(若余数长度较小,则在前面补0),另其置换出开始的3个0,得到一个新的信息码,这个码就是循环冗余码,发送方可以将此码发送给接收方,并根据提前约定好的多项式进行校验,如果相除为0,则说明数据无误,否则数据出现异常,需要重传。
关于模2除与模2减:建议大家看视频理解更轻松。点击这里。(5分50秒开始哈)
循环冗余码很重要,大家必须要掌握。
因为时间缘故,本来想好好做好笔记的,现在看来不太可能实现了,要抓紧时间准备计网了,这里先放一放。
原码乘法
补码乘法
原码除法
补码除法
浮点数运算
边栏推荐
- Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)
- mxnet导入报各种libcudart*.so、 libcuda*.so找不到
- [crampon programming] lintcode decoding Encyclopedia - 1100 strange printer
- 蛇形矩阵
- 取余操作是一个哈希函数
- [phantom engine UE] only six steps are needed to realize the deployment of ue5 pixel stream and avoid detours! (the principles of 4.26 and 4.27 are similar)
- Raki's notes on reading paper: soft gazetteers for low resource named entity recognition
- 假设检验——《概率论与数理统计》第八章学习笔记
- Power management bus (pmbus)
- Stage experience
猜你喜欢

TPG x AIDU|AI领军人才招募计划进行中!
![[phantom engine UE] only six steps are needed to realize the deployment of ue5 pixel stream and avoid detours! (the principles of 4.26 and 4.27 are similar)](/img/eb/a93630aff7545c6c3b71dcc9f5aa61.png)
[phantom engine UE] only six steps are needed to realize the deployment of ue5 pixel stream and avoid detours! (the principles of 4.26 and 4.27 are similar)
网络安全-记录web漏洞修复

如何优雅的获取每个分组的前几条数据

2022-2028 global and Chinese equipment as a Service Market Research Report

The remainder operation is a hash function
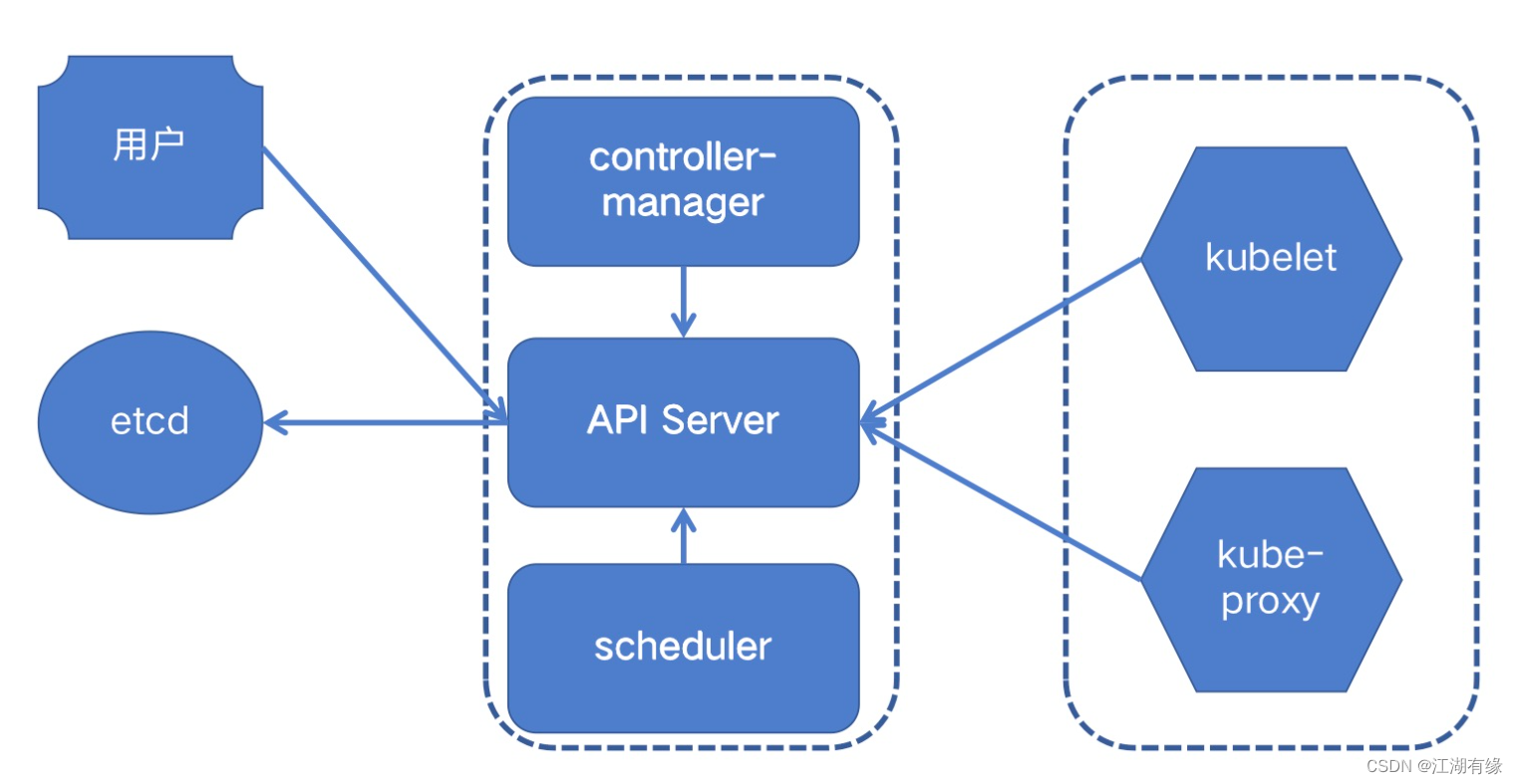
Scheduling system of kubernetes cluster
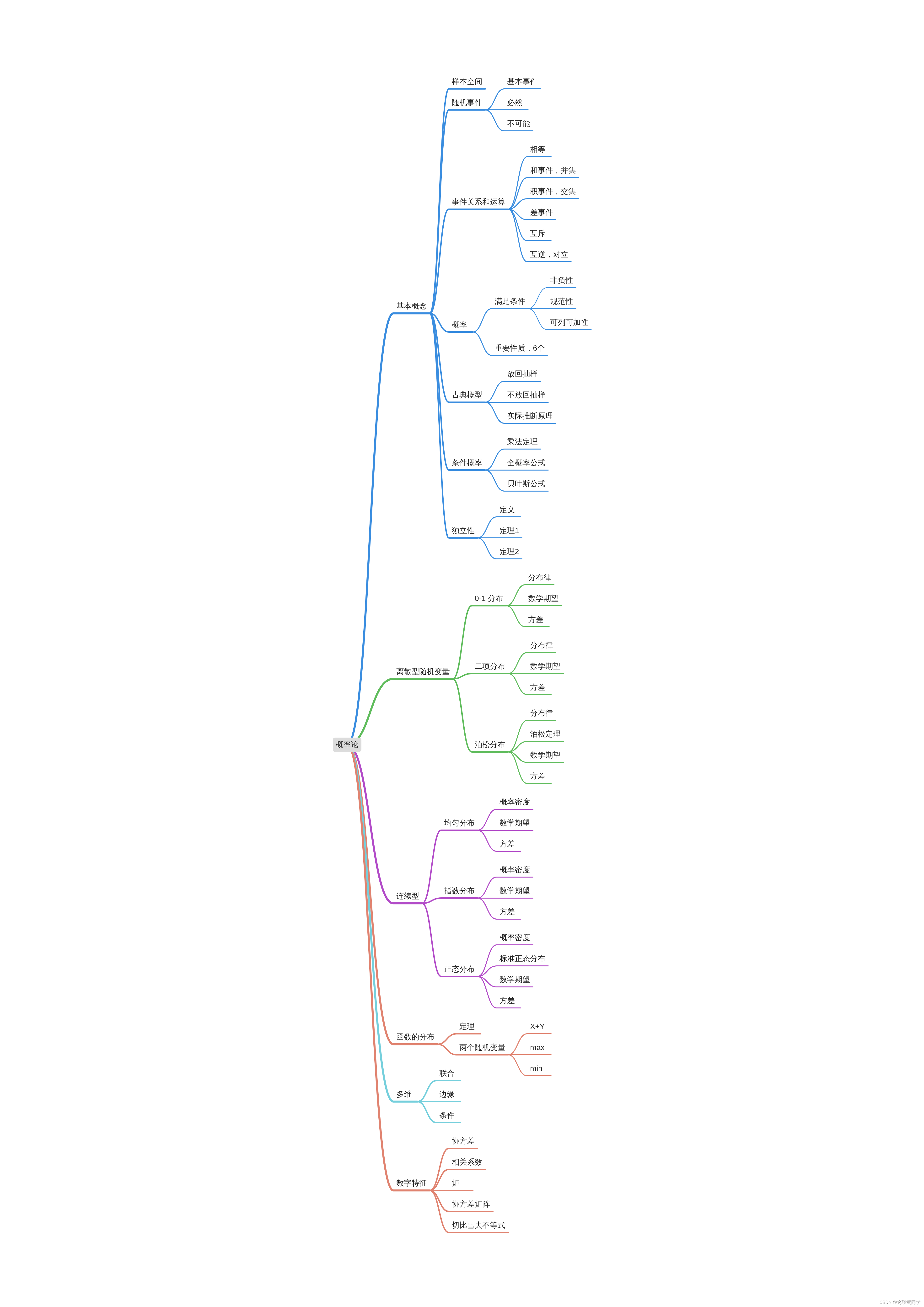
概率论与数理统计考试重点复习路线
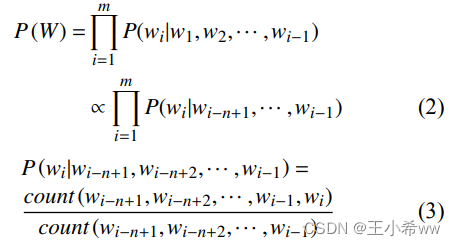
A survey of automatic speech recognition (ASR) research
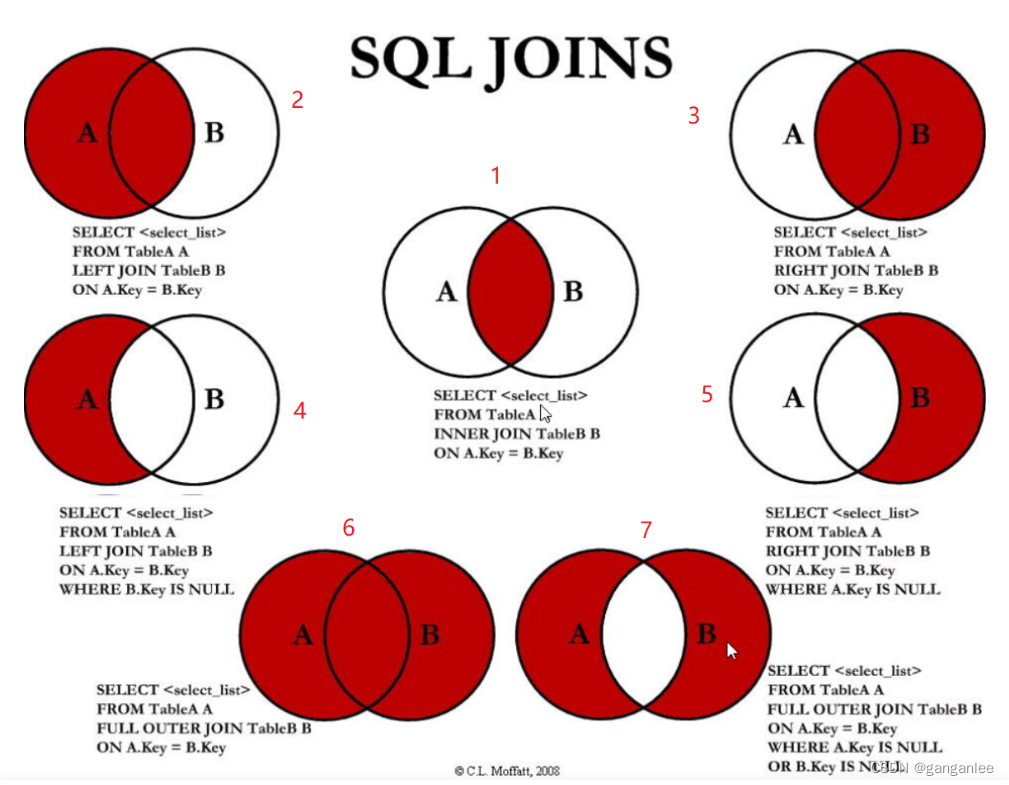
Seven join join queries of MySQL
随机推荐
Qt蓝牙:搜索蓝牙设备的类——QBluetoothDeviceDiscoveryAgent
如何进行「小步重构」?
Decimal to hexadecimal
官宣!第三届云原生编程挑战赛正式启动!
Reading and visualization of DICOM, MHD and raw files in medical imaging
A application wakes up B should be a fast method
如何优雅的获取每个分组的前几条数据
程序员应该怎么学数学
防护电路中的元器件
Un réveil de l'application B devrait être rapide
Raki's notes on reading paper: soft gazetteers for low resource named entity recognition
机器学习 --- 决策树
Managed service network: application architecture evolution in the cloud native Era
Introduction to RT thread kernel (4) -- clock management
The remainder operation is a hash function
A應用喚醒B應該快速方法
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
MacBook安装postgreSQL+postgis
[illusory engine UE] method to realize close-range rotation of operating objects under fuzzy background and pit recording
Fonction (sujette aux erreurs)