当前位置:网站首页>以赛促练-力扣第304场周赛反思(持续更新中)
以赛促练-力扣第304场周赛反思(持续更新中)
2022-08-02 20:51:00 【蒋大钊!】
这周主要在外面陪女朋友玩,自己整理图论存图方式等一些专题,其中几个最短路算法还不太熟练,但是今天在周赛上也依葫芦画瓢,用图论的解法解决了T3,心里还是蛮欣慰的。
这次又只AC了两题,T1和T3,说实话觉得自己编程能力还有较大空间,看到T1就是一脸懵逼,最后用个while(true)模拟过了,出来以后看到大佬的set做法就感觉自己对编程的掌握程度太拉了。看到T2继续懵逼,以为是回溯把所有情况找出来,问题是咱回溯也不熟练,出来以后看到大佬说是二分,可我之前明明做过二分训练的,还是不会,说明还没完全掌握二分思想。T3一看和我这周做的最短路算法好像,只要先存图然后把两个点的最短路求出来就可以,尝试一下果然过了,倍感欣慰。T4一看也是图论,但是我记得自己只会用拓扑排序检测图是否有环,但是没法统计环的大小,遂放弃。
最后成绩定格在2866 / 7372,什么时候才能稳定AC三题啊,看来还需要继续努力,同时将自己做过的整理彻底理解。
T1.使数组中所有元素都等于零
给你一个非负整数数组 nums 。在一步操作中,你必须:
选出一个正整数 x ,x 需要小于或等于 nums 中 最小 的 非零 元素。
nums 中的每个正整数都减去 x。
返回使 nums中所有元素都等于 0 需要的 最少 操作数。示例 1:
输入:nums = [1,5,0,3,5]
输出:3
解释: 第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。 第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。 第三步操作:选出 x = 2 ,之后 nums =[0,0,0,0,0] 。
示例 2:输入:nums = [0]
输出:0
解释:nums 中的每个元素都已经是 0 ,所以不需要执行任何操作。提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
我的做法,纯模拟:
class Solution {
public int minimumOperations(int[] nums) {
int len=nums.length;
int cnt=0;
while(true){
int min=101;
int max=-1;
int zero=0;
for(int i=0;i<len;i++){
if(nums[i]==0) zero++;
else{
min=Math.min(min,nums[i]);
max=Math.max(max,nums[i]);
}
}
//System.out.println(min+" "+max);
if(zero==len) return cnt;
else{
for(int i=0;i<len;i++){
if(nums[i]!=0)nums[i]-=min;
}
cnt++;
}
}
}
}
大佬的做法:由于每次操作都尽可能让数组中的非零最小值(可能有多个值)变为零,因此只需要统计数组中有多少个不同的非零值就可以了,所以用Set统计。
class Solution {
public int minimumOperations(int[] nums) {
HashSet<Integer> set=new HashSet<>();
for(int i:nums){
if(i!=0)set.add(i);
}
return set.size();
}
}
T2.分组的最大数量
给你一个正整数数组 grades ,表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组,其中分组间的顺序满足以下全部条件:
第 i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩,对所有组均成立(除了最后一组)。
第 i 个分组中的学生总数小于 第 (i + 1) 个分组中的学生总数,对所有组均成立(除了最后一组)。
返回可以形成的 最大 组数。示例 1:
输入:grades = [10,6,12,7,3,5]
输出:3
解释:下面是形成 3 个分组的一种可行方法:
- 第 1 个分组的学生成绩为 grades = [12] ,总成绩:12 ,学生数:1
- 第 2 个分组的学生成绩为 grades = [6,7] ,总成绩:6 + 7 = 13 ,学生数:2
- 第 3 个分组的学生成绩为 grades = [10,3,5] ,总成绩:10 + 3 + 5 = 18 ,学生数:3
可以证明无法形成超过 3 个分组。示例 2:
输入:grades = [8,8]
输出:1
解释:只能形成 1 个分组,因为如果要形成 2 个分组的话,会导致每个分组中的学生数目相等。提示:
1 <= grades.length <= 105
1 <= grades[i] <= 105
这题开始坐牢,怎么保证各组学生总成绩和各组总人数能够有序递增呢?又如何确定第一个分组的学生数量呢?
看别人题解还理解了半天,纯「贪心」,可以想象到要是组数最多,按人数1,2,3,4…这样子往上分就行了,最后没法分全的人补在最后一组。具体怎么分,那就贪心按照grades成绩从低到高分上去就行了,但是具体来说也不用想每组分数和怎么样,就只要满足人数的第二个要求,第一个要求自然满足了。二分查找满足k*(k+1)/2<=n的「最大k」就可以,这才是用到二分的地方。由此可见示例1给我们造成了多大的迷惑,按照这种从小到大从低到高的思想算出来的也是3组。
class Solution {
public int maximumGroups(int[] grades) {
int len=grades.length;
int left=1;
int right=len;
while(left<right){
int mid=(left+right+1)/2;
if(1L*mid*(mid+1)<=2*len){
left=mid;
}else{
right=mid-1;
}
}
return left;
}
}
或者就根据grades大小模拟分组:
class Solution {
public int maximumGroups(int[] grades) {
int len=grades.length;
//分组组数,也可以看做在没有最后补全情况下每组的人数
int i=0;
while(len-i>i){
len-=i;
i++;
}
return i;
}
}
T3.找到离给定两个节点最近的节点
这题就是求两点到其他所有节点的最短路径,然后遍历查找距离最短的那个节点就可以了。抽象出来就是两个「单源最短路」,我就很自然地想到了以前的Dijkstra,但是却不知道图论中的BFS也可以用于求「最短路径」,并且适用场景在加权有向图中,因此是知识树不完全,所以留个坑,准备这周做下BFS的专题,参考含泪总结周赛中的两道「图」问题,先贴上我的两遍堆优化的Dijkstra做法:
class Solution {
int INF=0x3f3f3f3f;
int N=(int)1e5+10;
int M=(int)1e5+10;
int[]head=new int[N];
int[]edge=new int[M];
int[]nextEdge=new int[M];
int[]w=new int[M];
int idx=0;
int n;
public void add(int a,int b,int c){
edge[idx]=b;
nextEdge[idx]=head[a];
head[a]=idx;
w[idx]=c;
idx++;
}
public int closestMeetingNode(int[] edges, int node1, int node2) {
n=edges.length;
Arrays.fill(head,-1);
for(int i=0;i<n;i++){
if(edges[i]!=-1)add(i,edges[i],1);
}
int[]dis1=new int[N];
boolean[]vis1=new boolean[N];
int[]dis2=new int[N];
boolean[]vis2=new boolean[N];
pqDijkstra(dis1,vis1,node1);
pqDijkstra(dis2,vis2,node2);
int ansDis=INF;
int ans=0;
for(int i=0;i<n;i++){
int max=Math.max(dis1[i],dis2[i]);
//System.out.println(dis1[i]+" "+dis2[i]);
if(max<ansDis){
ans=i;
ansDis=max;
}
}
return ansDis==INF?-1:ans;
}
public void pqDijkstra(int[]dis,boolean[]vis,int k){
Arrays.fill(vis,false);
Arrays.fill(dis,INF);
dis[k]=0;
PriorityQueue<int[]> que=new PriorityQueue<>((a,b)->a[1]-b[1]);
que.offer(new int[]{
k,0});
while(!que.isEmpty()){
int[]top=que.poll();
int id=top[0];
//进行访问标记与忽略
if(vis[id]) continue;
vis[id]=true;
for(int i=head[id];i!=-1;i=nextEdge[i]){
//和最短边相连的所有边,判断距离是否进行更新
int j=edge[i];
if(dis[j]>dis[id]+w[i]){
dis[j]=dis[id]+w[i];
//将原先为INF,现在已经被更新的点加入到que中
que.offer(new int[]{
j,dis[j]});
}
}
}
}
}
T4.图中的最长环
也是DFS和BFS在图中的应用,之前DFS只更新到二维平面上的搜索问题,因此确实不太熟练,因此需要把他们俩图相关的问题补上,先留下别人的题解,含泪总结周赛中的两道「图」问题,之后填坑。
边栏推荐
猜你喜欢
【SLAM】DM-VIO(ros版)安装和论文解读
A brief discussion on the transformation of .NET legacy applications
封装和包、访问修饰权限
软件成分分析:华为云重磅发布开源软件治理服务
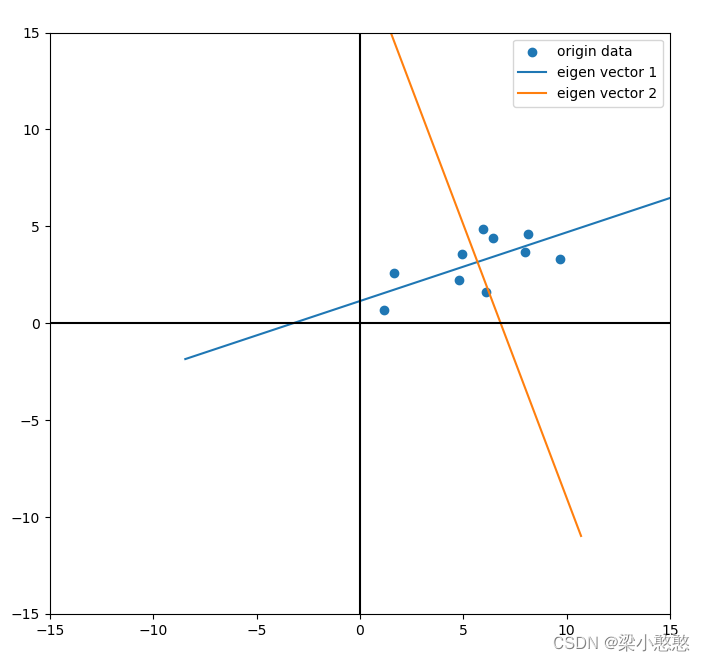
主成分分析(PCA)

Digital twins help visualize the construction of smart cities
SublimeText3 安装、配置项、包管理、常用必备插件、常用快捷键以及修改

信息学奥赛一本通(1259:【例9.3】求最长不下降序列)

《分布式微服务电商》专题(一)-项目简介
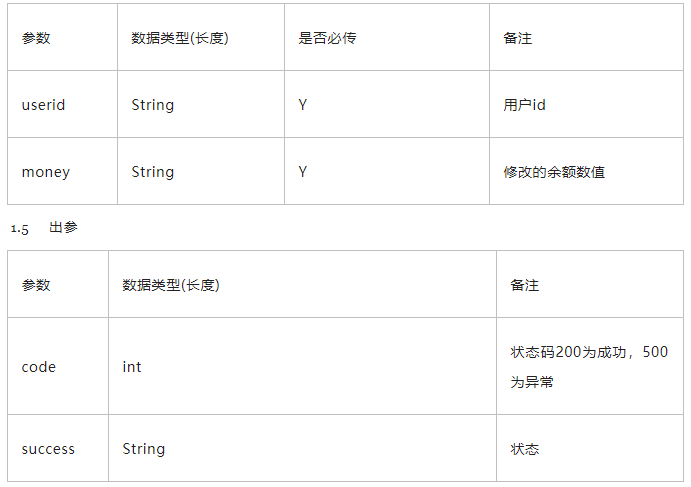
接口测试常用工具及测试方法(入门篇)
随机推荐
golang 刷leetcode:从栈中取出 K 个硬币的最大面值和
Bena's life cycle
接口测试常用工具及测试方法(入门篇)
golang刷letcode:公司命名
MSTP与STP
vscode如何能将输出从OUTPUT改为TERMINAL或者DebugConsole
js how to get the browser zoom ratio
《分布式微服务电商》专题(一)-项目简介
10 种最佳 IDE 软件 ,你更忠爱哪一个?
树形结构构造示例代码
典型相关分析CCA计算过程
C# Barrier类
软件测试的流程规范有哪些?具体要怎么做?
传感器工作原理
解道7-编程技术4
[C题目]力扣142. 环形链表 II
Day35 LeetCode
Bena的生命周期
「每周译Go」这次我们来点不一样的!--《How to Code in Go》系列上线
golang刷leetcode:最大波动的子字符串
