当前位置:网站首页>Atcoder beginer contest 254 "e BFS" f st table maintenance differential array GCD "
Atcoder beginer contest 254 "e BFS" f st table maintenance differential array GCD "
2022-07-05 10:18:00 【Chels.】
AtCoder Beginner Contest 254
E - Small d and k
Title Description :
Here's an undirected graph , The degree of each point is at most 3, Conduct Q Time to ask , Give it every time you ask
x,k, Means to ask withxAs a starting point , Distance less than or equal tokStep by stepidAndamong
k<=3
Ideas :
Because the degree is at most 3, And
k<=3, So each inquiry involves at most 27 A little bit ,27 * Q Only then 4e6, Complexity makes sense , We run violently bfs Just go
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define mod7 1000000007
#define mod9 998244353
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;
#define MAX 300000 + 50
int n, m, k, x, y;
vector<int>G[MAX];
bool vis[MAX];
void work(){
cin >> n >> m;
for(int i = 1; i <= m; ++i){
cin >> x >> y;
G[x].push_back(y);
G[y].push_back(x);
}
cin >> m;
while(m--){
cin >> x >> k;
if(k == 0){
cout << x << endl;
continue;
}
vector<int>v;
queue<pii>q;
q.push(m_p(x, k));
vis[x] = 1;
while(!q.empty()){
auto [u, d] = q.front();q.pop();
v.push_back(u);
// cout << u << ' ' << d << endl;
for(auto v : G[u]){
if(!vis[v] && d){
q.push(m_p(v, d - 1));
vis[v] = 1;
}
}
}
int ans = 0;
for(auto x : v){
ans += x;
vis[x] = 0;
}
cout << ans << endl;
}
}
int main(){
io;
work();
return 0;
}
F - Rectangle GCD
Title Description :
Here are two arrays
ar,br, All the lengths aren, Order one by onen*nMatrix C, amongC[i][j] = ar[i] + br[j], Now here you areQTime to ask , Each time you ask, I will give you the upper left and lower right corners of a small rectangle , Ask all the elements of this small rectangle gcd
Ideas :
First of all, it should be clear that the maximum common divisor of all elements of a sequence is equal to the maximum common divisor of the difference group , namely g c d ( a [ 1 ] , a [ 2 ] , . . . , a [ n ] ) = g c d ( a [ 1 ] , a [ 2 ] − a [ 1 ] , a [ 3 ] − a [ 2 ] , . . . , a [ n ] − a [ n − 1 ] ) gcd(a[1], a[2], ...,a[n]) = gcd(a[1], a[2] - a[1], a[3] - a[2], ... ,a[n] - a[n - 1]) gcd(a[1],a[2],...,a[n])=gcd(a[1],a[2]−a[1],a[3]−a[2],...,a[n]−a[n−1])
So let's consider the first
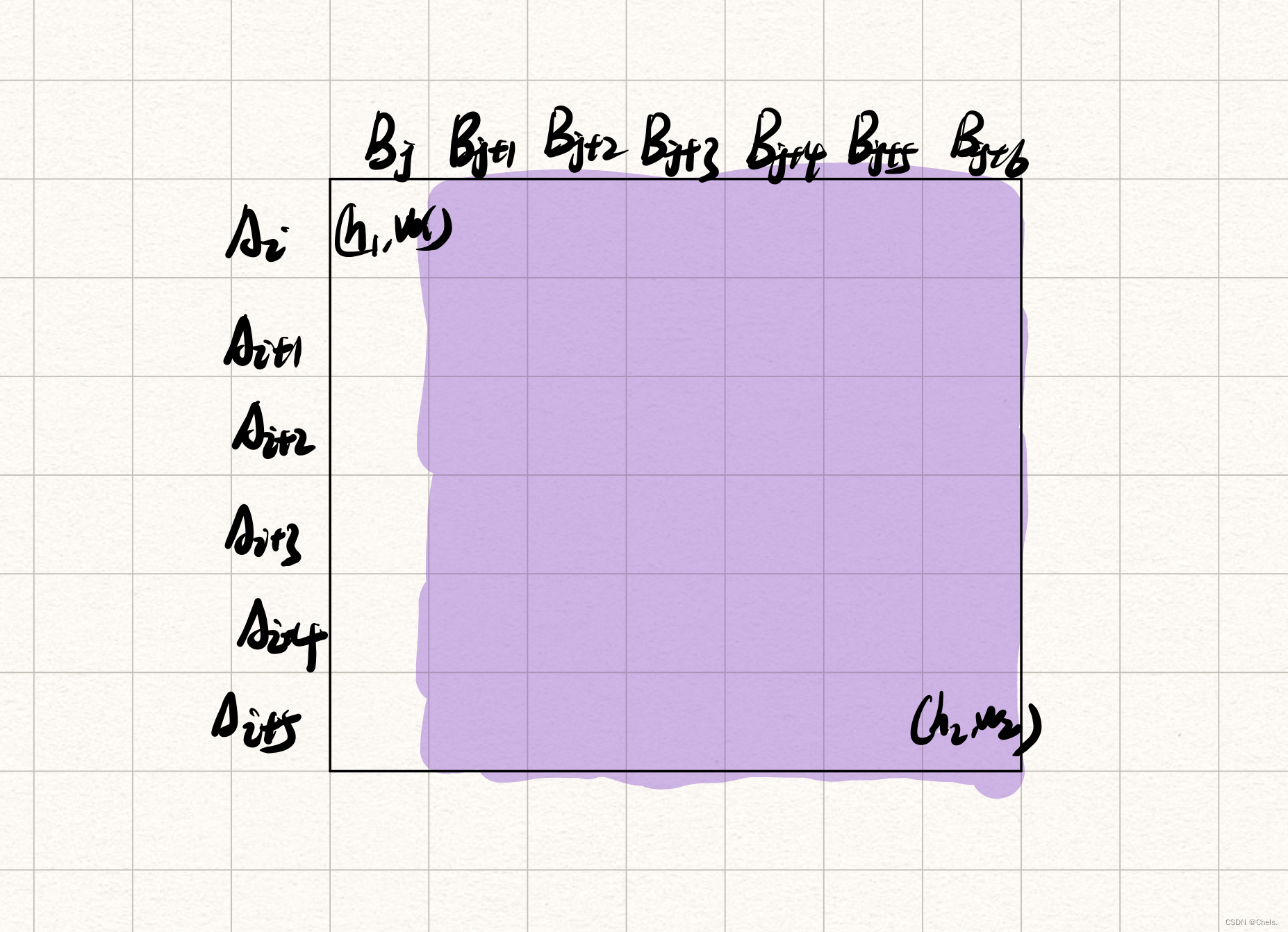
iThat's okg c d ( a [ i ] + b [ j ] , a [ i + 1 ] + b [ j ] , a [ i + 2 ] + b [ j ] , . . . . ) = g c d ( a [ i ] + b [ j ] , a [ i + 1 ] − a [ i ] , a [ i + 2 ] − a [ i + 1 ] . . . ) gcd(a[i]+b[j], a[i + 1]+b[j], a[i + 2]+b[j],....) = gcd(a[i] + b[j], a[i + 1]-a[i], a[i + 2] - a[i + 1]...) gcd(a[i]+b[j],a[i+1]+b[j],a[i+2]+b[j],....)=gcd(a[i]+b[j],a[i+1]−a[i],a[i+2]−a[i+1]...) Let's not watch first
a[i]+b[j], According to the following paragraph gcd, We can do this by askinggcd(a[i+1]-a[i], a[i+2]-a[i+1]...)Get all the numbers in the purple part of the figure below gcd
Empathy , We can use
gcd(br[i+1]-br[i], br[i+2]-br[i+1]....)Get all the numbers in the blue part below gcd
What we need is from
C[h1][w1]ToC[h2][w2]Of all numbers gcd, By synthesizing the pattern, we can find that the number in the upper left corner has not been calculated , So we only need to divide the difference between the above two partitions gcd andC[h1][w2]That is to sayA[h1]+B[w1]Ask for one gcd that will doSo we can use st Table to maintain the interval of the difference group gcd
To be honest, I didn't think so deeply when I wrote , I think of it.
gcd(x, y)It can be converted intogcd(x-y, x), I think it's the difference groupgcd, In addition, it is not enough to calculate the difference fraction Group , There has to be ax, Just add the elements in the upper left corner, and the three find a gcd, Recite one st I didn't expect it to be over
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define mod7 1000000007
#define mod9 998244353
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;
#define MAX 300000 + 50
int n, m, k, x;
ll ar[MAX];
ll br[MAX];
ll gcd(ll a, ll b){
if(b) return gcd(b, a % b);
else return a;
}
ll lg[MAX];
ll g1[MAX][22];
ll g2[MAX][22];
void init(){
for(int i = 2; i <= n; ++i){
lg[i] = lg[i / 2] + 1;
}
for(int i = 2; i <= n; ++i){
g1[i][0] = ar[i] - ar[i - 1];
g2[i][0] = br[i] - br[i - 1];
}
for(int j = 1; j <= lg[n]; ++j){
for(int i = 2; i + (1 << j) - 1 <= n; ++i){
g1[i][j] = gcd(g1[i][j - 1], g1[i + (1 << (j - 1))][j - 1]);
g2[i][j] = gcd(g2[i][j - 1], g2[i + (1 << (j - 1))][j - 1]);
}
}
}
ll get_gcd(int l, int r, int op){
ll d = lg[r - l + 1];
if(op)return abs(gcd(g1[l][d], g1[r - (1 << d) + 1][d]));
else return abs(gcd(g2[l][d], g2[r - (1 << d) + 1][d]));
}
void work(){
cin >> n >> m;
for(int i = 1; i <= n; ++i)cin >> ar[i];
for(int j = 1; j <= n; ++j)cin >> br[j];
init();
int h1, h2, w1, w2;
while(m--){
cin >> h1 >> h2 >> w1 >> w2;
ll a = 0, b = 0;
if(h1 == h2)a = 0;
else a = get_gcd(h1 + 1, h2, 1);
if(w1 == w2)b = 0;
else b = get_gcd(w1 + 1, w2, 0);
cout << gcd(a, gcd(b, ar[h1] + br[w1])) << endl;
}
}
int main(){
io;
work();
return 0;
}
边栏推荐
- Tianlong Babu TLBB series - about items dropped from packages
- flink cdc不能监听mysql日志,大家遇到过这个问题吧?
- 一种用于干式脑电图的高密度256通道电极帽
- DDOS攻击原理,被ddos攻击的现象
- leetcode:1200. 最小绝对差
- How to judge that the thread pool has completed all tasks?
- Redis如何实现多可用区?
- 《通信软件开发与应用》课程结业报告
- 请问postgresql cdc 怎么设置单独的增量模式呀,debezium.snapshot.mo
- Excerpt from "sword comes" (VII)
猜你喜欢

苹果 5G 芯片研发失败?想要摆脱高通为时过早

RMS to EAP is simply implemented through mqtt
Kotlin compose multiple item scrolling

To bring Euler's innovation to the world, SUSE should be the guide

StaticLayout的使用详解
硬核,你见过机器人玩“密室逃脱”吗?(附代码)

Today in history: the first e-book came out; The inventor of magnetic stripe card was born; The pioneer of handheld computer was born

高级 OpenCV:BGR 像素强度图
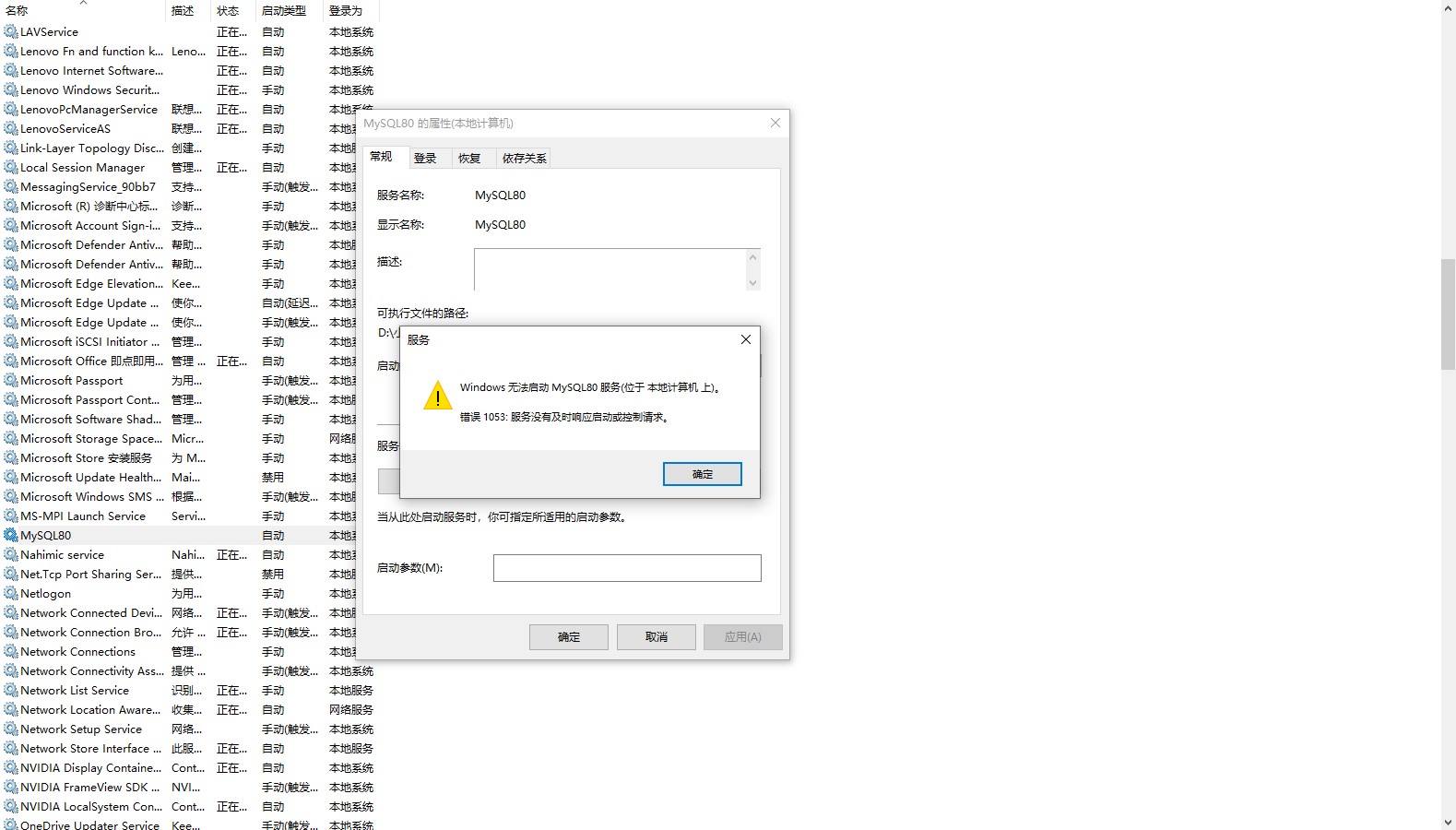
Mysql80 service does not start
Unity粒子特效系列-毒液喷射预制体做好了,unitypackage包直接用 -下
随机推荐
flink cdc不能监听mysql日志,大家遇到过这个问题吧?
How to judge that the thread pool has completed all tasks?
程序员搞开源,读什么书最合适?
Jupiter notebook shortcut key
[tips] get the x-axis and y-axis values of cdfplot function in MATLAB
The Alipay in place function can't be found, and the Alipay in place function is offline
如何判断线程池已经执行完所有任务了?
Energy momentum: how to achieve carbon neutralization in the power industry?
Personal website construction tutorial | local website environment construction | website production tutorial
请问大佬们 有遇到过flink cdc mongdb 执行flinksql 遇到这样的问题的么?
StaticLayout的使用详解
钉钉、企微、飞书学会赚钱了吗?
@JsonAdapter注解使用
横向滚动的RecycleView一屏显示五个半,低于五个平均分布
Workmanager Learning one
Workmanager learning 1
Tianlong Babu TLBB series - questions about skill cooling and the number of attack ranges
Unity particle special effects series - the poison spray preform is ready, and the unitypackage package can be used directly - next
Unity粒子特效系列-毒液喷射预制体做好了,unitypackage包直接用 -下
Implementation of smart home project
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-KgJeB0Cd-1656599477903)(/Users/chelsea/Library/Application Support/typora-user-images/image-20220630222632492.png)]](/img/ef/a7ccf6d88729b3e5f3419e30914267.png)