当前位置:网站首页>二分图判定
二分图判定
2022-07-06 14:26:00 【AC__dream】
先来说一下什么是二分图,对于一个图,我们将其顶点集分为两部分A和B,从而使得任意一条边的两个顶点一个在A中一个在B中,而不会出现一条边的两个顶点全部在A中或全部在B中这种情况。
先来说一个定理:一个图是二分图当且仅当这个图中不存在奇数环,也就是不存在一个环的顶点个数是奇数个。
如果利用这个定理来判定一个图是不是二分图的话那么我们就可以使用染色的方法来进行实现,就是每一条边的两个顶点的颜色一定是不相同的,我们按照这个原则来对图进行染色,如果染色成功那么这个图就是一个二分图,否则就不是一个二分图。
给出一道例题及其代码实现:

输入样例:
4 4
1 3
1 4
2 3
2 4输出样例:
Yes代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
using namespace std;
const int N=2e5+10;
int h[N],e[N],ne[N],color[N],idx;
//color[i]代表第i个节点的颜色
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
bool dfs(int x,int c)
{
color[x]=c;
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(color[j]!=-1)//j节点已经染过颜色
{
if(color[j]==c) return false;//一条边的两个顶点颜色相同,矛盾
}
else if(!dfs(j,c^1)) return false;//发现矛盾
}
return true;//所有节点都没有发现矛盾就返回真
}
int main()
{
int n,m;
cin>>n>>m;
memset(h,-1,sizeof h);
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
memset(color,-1,sizeof color);//初始颜色为-1
bool flag=true;
for(int i=1;i<=n;i++)
{
if(color[i]==-1)
{
if(!dfs(i,1))//将当前点染成1号颜色
{
flag=false;//出现奇数环就直接退出
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}边栏推荐
- About the professional ethics of programmers, let's talk about it from the way of craftsmanship and neatness
- 中国1,4-环己烷二甲醇(CHDM)行业调研与投资决策报告(2022版)
- MySQL related terms
- What a new company needs to practice and pay attention to
- Applet system update prompt, and force the applet to restart and use the new version
- 3DMAX assign face map
- Shortcut keys in the terminal
- 设置状态栏样式Demo
- Support multiple API versions in flask
- What is the difference between animators and animators- What is the difference between an Animator and an Animation?
猜你喜欢
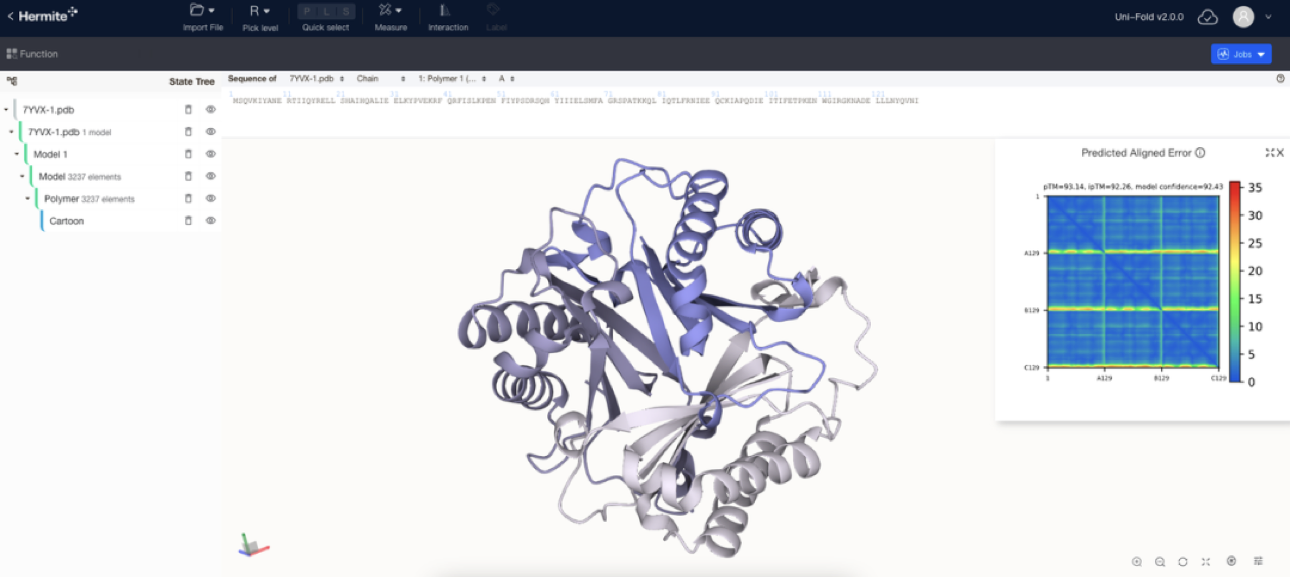
AI 企业多云存储架构实践 | 深势科技分享
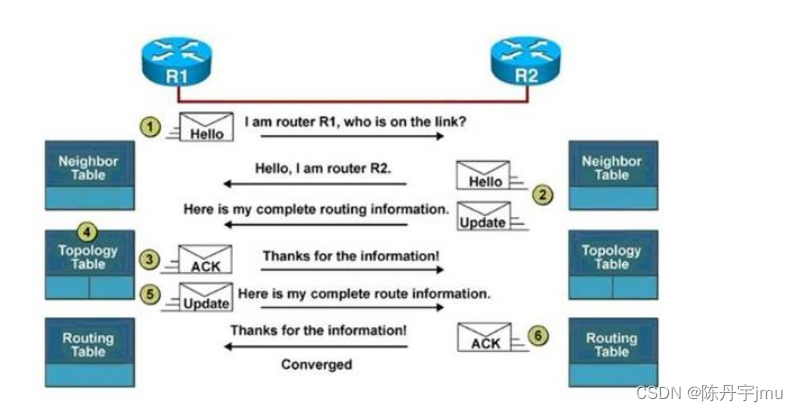
CCNA Cisco network EIGRP protocol
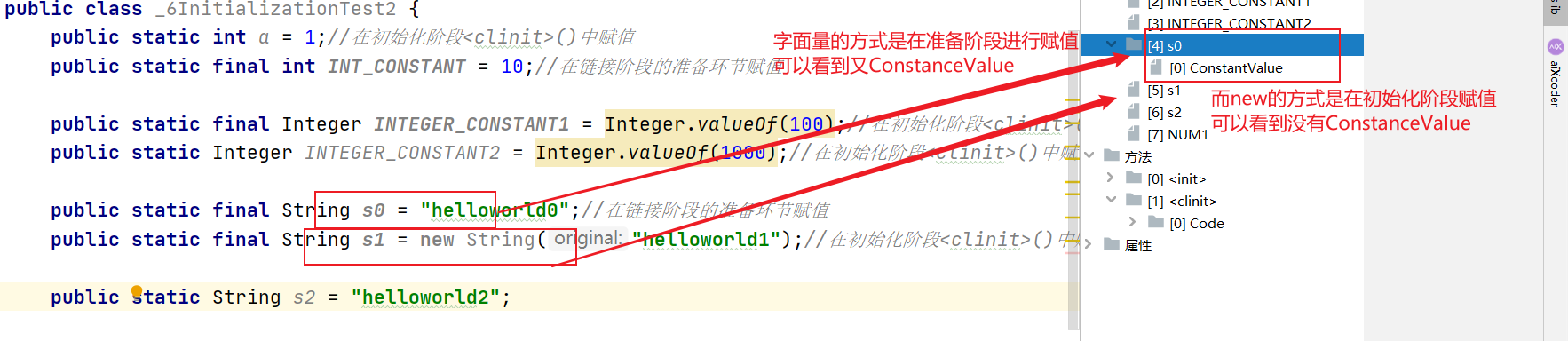
Chapter 3: detailed explanation of class loading process (class life cycle)
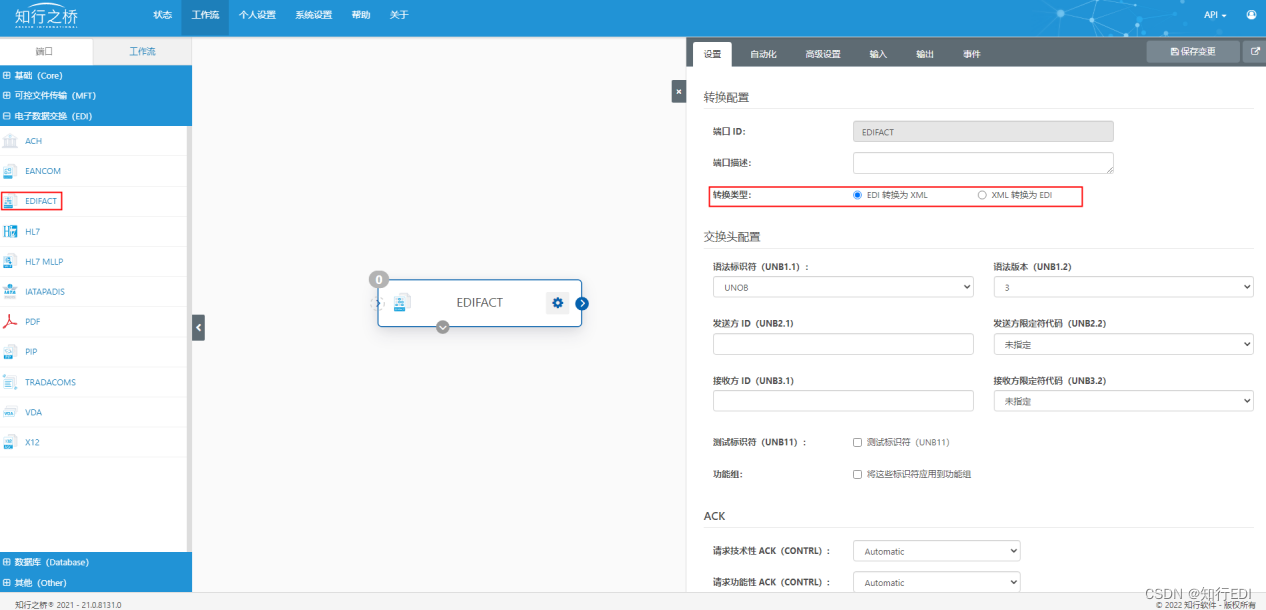
PVL EDI 项目案例

GPS du début à l'abandon (XIII), surveillance autonome de l'intégrité du récepteur (raim)

重磅新闻 | Softing FG-200获得中国3C防爆认证 为客户现场测试提供安全保障
Classic sql50 questions
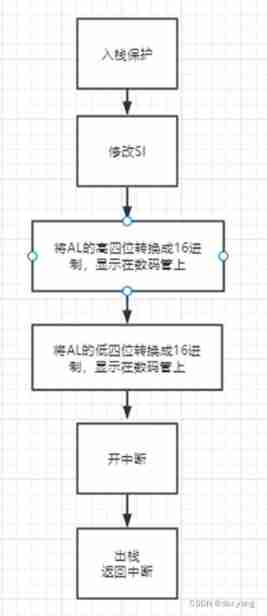
Assembly and Interface Technology Experiment 6 - ADDA conversion experiment, AD acquisition system in interrupt mode

C#实现水晶报表绑定数据并实现打印4-条形码

Oracle control file and log file management
随机推荐
C#实现水晶报表绑定数据并实现打印4-条形码
Unity3D学习笔记6——GPU实例化(1)
Hardware development notes (10): basic process of hardware development, making a USB to RS232 module (9): create ch340g/max232 package library sop-16 and associate principle primitive devices
新入职一家公司需要去实践和注意的内容
Write a rotation verification code annotation gadget with aardio
Data processing skills (7): MATLAB reads the data in the text file TXT with mixed digital strings
Oracle Performance Analysis 3: introduction to tkprof
功能强大的国产Api管理工具
Research and investment strategy report of China's VOCs catalyst industry (2022 Edition)
How does the uni admin basic framework close the creation of super administrator entries?
AI enterprise multi cloud storage architecture practice | Shenzhen potential technology sharing
Notes de développement du matériel (10): flux de base du développement du matériel, fabrication d'un module USB à RS232 (9): création de la Bibliothèque d'emballage ch340g / max232 SOP - 16 et Associa
What is the difference between animators and animators- What is the difference between an Animator and an Animation?
NetXpert XG2帮您解决“布线安装与维护”难题
Adjustable DC power supply based on LM317
Powerful domestic API management tool
数据处理技巧(7):MATLAB 读取数字字符串混杂的文本文件txt中的数据
Codeforces Round #274 (Div. 2) –A Expression
解决项目跨域问题
2500个常用中文字符 + 130常用中英文字符