当前位置:网站首页>Computer composition and design work05 ——fifth verson
Computer composition and design work05 ——fifth verson
2022-06-12 06:25:00 【JamSlade】
Computer Composition and Design Homework 5
3.20
[5] <§3.5> What decimal number does the bit pattern 0×0C000000 represent if it is a two’s complement integer? An unsigned integer?
- The first is 0, If it is int Type then the description is a positive sign ,
The calculation process is
C ( 12 ) × 1 6 6 = 201 , 326 , 592 C(12)\times 16^6 = 201,326,592 C(12)×166=201,326,592 - unsigned int The calculation is the same as above
3.22
[10] <§3.5> What decimal number does the bit pattern 0×0C000000 represent if it is a floating point number? Use the IEEE 754 standard
Expressed as 2 Into the system for
0 ( operator Number position ) 00011000 ( finger Count position ) 0000000000 0000000000 000 ( Small Count Ministry branch ) 0\ ( Sign bit ) 00011000\ ( Exponential position )0000000000\ 0000000000\ 000( The fractional part ) 0 ( operator Number position )00011000 ( finger Count position )0000000000 0000000000 000( Small Count Ministry branch )
It is not difficult to find that this number is positive , And the offset is 24 - 127 = -103
So the number is 1.0 × 2 − 103 1.0\times 2^{-103} 1.0×2−103
3.23
[10] <§3.5> Write down the binary representation of the decimal number
63.25 assuming the IEEE 754 single precision format
63.25 Binary representation as
111111.01 = 1.1111101 × 2 5 111111.01 = 1.1111101\times 2^{5} 111111.01=1.1111101×25
127+5 = 132 = 10000100(2)
The expression is as follows
0 10000100 1111101000 0000000000 000 0\quad 10000100\quad 1111101000\ 0000000000\ 000 0100001001111101000 0000000000 000
3.24
[10] <§3.5> Write down the binary representation of the decimal number
63.25 assuming the IEEE 754 double precision format.
1023+5 = 1028 = 10000000100(2)
0 10000000100 1111101000 0000000000 0000000000 0000000000 0000000000 00 0\quad 10000000100\quad 1111101000\ 0000000000\ 0000000000\ 0000000000\ 0000000000\ 00 0100000001001111101000 0000000000 0000000000 0000000000 0000000000 00
3.25
[10] <§3.5> Write down the binary representation of the decimal number
63.25 assuming it was stored using the single precision IBM format (base 16,
instead of base 2, with 7 bits of exponent).
63.25 = 111111.01 ( 2 ) = 3 F . 40 ( 16 ) = 0.3 F 40 × 1 6 2 63.25 = 111111.01(2) = 3F.40(16) = 0.3F40\times16^2 63.25=111111.01(2)=3F.40(16)=0.3F40×162
Sign bit is 0, Exponential position 63 + 2 = 1000001 ( 2 ) 63+2 = 1000001(2) 63+2=1000001(2)
0 1000001 1111101000 0000000000 000 0\quad\ 1000001\quad 1111101000\ 0000000000\ 000 0 10000011111101000 0000000000 000
Look at the answer. It seems that the exponent is 64+2, I have doubts about this , Index 127 Used to indicate overflow ,0 Express 0, I think so 63 As an intermediate quantity
3.26
[20] <§3.5> Write down the binary bit pattern to represent − 1.5625 × 1 0 − 1 -1.5625 \times 10^{-1} −1.5625×10−1assuming a format similar to that employed by the DEC PDP-8 (the left most 12 bits are the exponent stored as a two’s complement number, and the rightmost 24 bits are the fraction stored as a two’s complement number). No hidden 1 is used. Comment on how the range and accuracy of this 36-bit pattern compares to the single and double precision IEEE 754 standards.
− 1.5625 × 1 0 − 1 = − 0.15625 = − 0.00101 ( 2 ) = − 0.101 × 2 − 2 -1.5625 \times 10^{-1} = -0.15625 = -0.00101(2) = -0.101\times2^{-2} −1.5625×10−1=−0.15625=−0.00101(2)=−0.101×2−2
So the index 2 use repair code surface in by 000000000010 , − 2 by 111111111110 2 Represented by a complement as 000000000010,-2 by 111111111110 2 use repair code surface in by 000000000010,−2 by 111111111110
The general expression is
111111111110 ( 12 position ) 101000000000 000000000000 ( 24 position ) 111111111110(12 position )\quad101000000000\quad000000000000(24 position ) 111111111110(12 position )101000000000000000000000(24 position )
- The index can be expressed as − 2048 ∼ 2047 -2048\sim2047 −2048∼2047
- The base number can express 2 − 24 ∼ 1 − 2 − 24 2^{-24}\sim 1-2^{-24} 2−24∼1−2−24
| DEC PDP-8 | Single precision | Double precision | |
| Minimum positive number | 2 − 24 × 2 − 2048 2^{-24}\times2^{-2048} 2−24×2−2048 | 1 × 2 − 126 1\times2^{-126} 1×2−126 | 1 × 2 − 1022 1\times2^{-1022} 1×2−1022 |
| Maximum positive number | ( 1 − 2 − 24 ) × 2 2047 (1-2^{-24})\times2^{2047} (1−2−24)×22047 | ( 1 + 1 − 2 23 ) × 2 127 (1+1-2^{23})\times2^{127} (1+1−223)×2127 | ( 1 + 1 − 2 52 ) × 2 1023 (1+1-2^{52})\times2^{1023} (1+1−252)×21023 |
Should be DEC PDP-8 Can represent a wider range of
3.27
[20] <§3.5> IEEE 754-2008 contains a half precision that is only 16 bits
wide. Th e left most bit is still the sign bit, the exponent is 5 bits wide and has a bias
of 15, and the mantissa is 10 bits long. A hidden 1 is assumed. Write down the
bit pattern to represent − 1.5625 × 1 0 − 1 -1.5625 \times 10^{-1} −1.5625×10−1
assuming a version of this format, which
uses an excess-16 format to store the exponent. Comment on how the range and
accuracy of this 16-bit fl oating point format compares to the single precision IEEE
754 standard.
− 1.5625 × 1 0 − 1 = − 0.15625 = − 0.00101 ( 2 ) = − 1.01 × 2 − 3 -1.5625 \times 10^{-1} = -0.15625 = -0.00101(2) = -1.01\times2^{-3} −1.5625×10−1=−0.15625=−0.00101(2)=−1.01×2−3
- Symbol bit 1 A negative number
- The expressible part of the index is 1-30, The offset for the 15, So the index is 12(01100) Express -3
- The base part is marked with 0100 0000 00
1 01100 0100000000 1\quad 01100\quad 0100000000 1011000100000000
3.29
[20] <§3.5> Calculate the sum of 2.6125 × 1 0 1 2.6125\times 10^1 2.6125×101and 4.150390625 × 1 0 − 1 4.150390625\times 10^{-1} 4.150390625×10−1by hand, assuming A and B are stored in the 16-bit half precision described in Exercise 3.27. Assume 1 guard, 1 round bit, and 1 sticky bit, and round to the nearest even. Show all the steps.
2.6125 × 1 0 1 = 26.125 = 1.1010001 × 2 4 2.6125 \times 10^1=26.125 = 1.1010001\times 2^4 2.6125×101=26.125=1.1010001×24
4.150390625 × 1 0 − 1 = 1.1010100111 × 2 − 2 4.150390625\times 10^{-1} = 1.1010100111\times 2^{-2} 4.150390625×10−1=1.1010100111×2−2
Move to the left 6 Bits to align exponents
So there is ( Note that the half precision is only 11 Bits are used to save )
1.1010001000
1.0000011010100111 / It should be noted that the beginning is 1, The rest needs to be left out
1.1010100010
Extra bits ( Yes 6 position ) More than significant digits (11) Half a bit , It should be carry
Last
1.1010100011 ( Into the position ) × 2 4 = 26.546875 1.1010100011( carry )\times 2^4 = 26.546875 1.1010100011( Into the position )×24=26.546875
3.32
[20] <§3.9> Calculate ( 3.984375 × 1 0 − 1 + 3.4375 × 1 0 − 1 ) + 1.771 × 1 0 3 (3.984375 \times 10^{-1} + 3.4375\times 10^{-1})+ 1.771 \times 10^3 (3.984375×10−1+3.4375×10−1)+1.771×103by hand, assuming each of the values are stored in the 16-bit half precision format described in Exercise 3.27 (and also described in the text). Assume 1 guard, 1 round bit, and 1 sticky bit, and round to the nearest even. Show all the steps, and write your answer in both the 16-bit fl oating point format and in decimal.
Keep a (Guard bit)、 Approximate position (Round bit) And viscous position (Sticky bit).
Keep a : The lowest point after approximation
Approximate position : The last of the reserved bits
Sticky bits : All bits after the approximate bit are treated as one bit after or operation
3.984375 × 1 0 − 1 = 1.1001100000 × 2 − 2 3.984375 \times 10^{-1} = 1.1001100000\times 2^{-2} 3.984375×10−1=1.1001100000×2−2
3.4375 × 1 0 − 1 = 1.0110000000 × 2 − 2 3.4375\times 10^{-1} =1.0110000000\times 2^{-2} 3.4375×10−1=1.0110000000×2−2
1.771 × 1 0 3 = 1.1011101011 × 2 10 1.771 \times 10^3 = 1.1011101011\times 2^{10} 1.771×103=1.1011101011×210
| (A) | 1.1001100000 | × 2 − 2 \times 2^{-2} ×2−2 |
| (B)+ | 1.0110000000 | × 2 − 2 \times 2^{-2} ×2−2 |
| = | 10.1111100000 | × 2 − 2 \times 2^{-2} ×2−2 |
| = | 1.0111110000 | × 2 − 1 \times 2^{-1} ×2−1 |
| (A+B) | 1.0111110000 | × 2 − 1 \times 2^{-1} ×2−1 |
| = | 0.000000000010111110000 | × 2 10 \times 2^{10} ×210 |
| C | 1.1011101011 | × 2 10 \times 2^{10} ×210(A+B The superfluous part is 101, exceed 0.5, Should carry ) |
| (A+B)+C= | 1.1011101100 | × 2 10 \times 2^{10} ×210 |
| = | 1772 |
3.33
[20] <§3.9> Calculate 3.984375 × 1 0 − 1 + ( 3.4375 × 1 0 − 1 + 1.771 × 1 0 3 ) 3.984375 \times 10^{-1} + (3.4375 \times 10^{-1} + 1.771 \times 10^3) 3.984375×10−1+(3.4375×10−1+1.771×103)by hand, assuming each of the values are stored in the 16-bit half precision format described in Exercise 3.27 (and also described in the text). Assume 1 guard, 1 round bit, and 1 sticky bit, and round to the nearest even. Show all the steps, and write your answer in both the 16-bit fl oating point format and in decimal.
3.984375 × 1 0 − 1 = 1.1001100000 × 2 − 2 3.984375 \times 10^{-1} = 1.1001100000\times 2^{-2} 3.984375×10−1=1.1001100000×2−2
3.4375 × 1 0 − 1 = 1.0110000000 × 2 − 2 3.4375\times 10^{-1} =1.0110000000\times 2^{-2} 3.4375×10−1=1.0110000000×2−2
1.771 × 1 0 3 = 1.1011101011 × 2 10 1.771 \times 10^3 = 1.1011101011\times 2^{10} 1.771×103=1.1011101011×210
| (B) | 0.0000000000010110000000 | × 2 10 \times 2^{10} ×210 |
| + | 1.1011101011 | × 2 10 \times 2^{10} ×210 |
| = | 1.1011101011 | × 2 10 \times 2^{10} ×210 |
| (A) | 0.0000000000011001100000 | × 2 10 \times 2^{10} ×210 |
| + | 1.1011101011 | × 2 10 \times 2^{10} ×210 |
| = | 1.1011101011 | × 2 10 \times 2^{10} ×210 |
| = | 1771 |
3.34
[10] <§3.9> Based on your answers to 3.32 and 3.33, does ( 3.984375 × 1 0 − 1 + 3.4375 × 1 0 − 1 ) + 1.771 × 1 0 3 = 3.984375 × 1 0 − 1 + ( 3.4375 × 1 0 − 1 + 1.771 × 1 0 3 ) (3.984375 \times 10^{-1} + 3.4375 \times 10^{-1}) + 1.771 \times 10^3 = 3.984375 \times 10^{-1} + (3.4375\times 10^{-1} + 1.771 \times10^3) (3.984375×10−1+3.4375×10−1)+1.771×103=3.984375×10−1+(3.4375×10−1+1.771×103)?
Is not the same , The first is 1772
The second is 1771
The exact solution should be 1771.742187
边栏推荐
猜你喜欢

cv2.fillPoly coco annotator segment坐标转化为mask图像
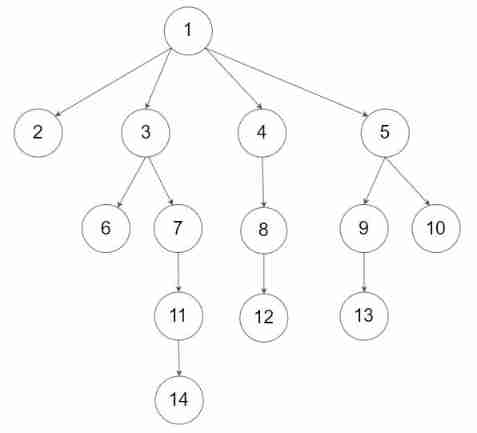
LeetCode-1490. Clone n-ary tree

Analysis of memory management mechanism of (UE4 4.26) UE4 uobject

QT--实现TCP通信

Redis basic notes

Leetcode January 12 daily question 334 Increasing ternary subsequence

Use ms17-010 Eternal Blue vulnerability to infiltrate win7 and establish a permanent back door

Sensor bringup 中的一些问题总结

Unity implements smooth interpolation

About session Getattribute, getattribute error
随机推荐
Overview of camera image quality
leetcode 35. Search insert location
Book classification based on Naive Bayes
Nodemon cannot load the file c:\users\administrator\appdata\roaming\npm\nodemon PS1, because script execution is prohibited in this system
torch在高版本训练的模型在低版本中使用报错
LeetCode-997. Find the town judge
Unity3d script captures a sub area from the screen and saves it as texture2d, which is used to save pictures and maps
Zip and Items() difference
LeetCode-1873. Calculate special bonus
MLP sensor
Nocturnal simulator ADB view log
Multithreading (V) -- Concurrent tools (II) -- j.u.c concurrent contracting (I) -- AQS and reentrantlock principles
(UE4 4.27) UE4 adds a customized meshpass to realize the edge illumination of the mobile terminal
Word vector training based on nnlm
C # converts the hexadecimal code form of text to text (ASCII)
LeetCode-剑指Offer(第二版)个人题解完整版
(UE4 4.27) customize globalshader
JS pre parsing
LeetCode-1741. Find total time spent per employee
English语法_副词_有无ly,意义不同