What is AVL tree?

---

One . What is? AVL Trees

To know AVL Before tree, let's know what a binary search tree is :

1. Binary search tree

Binary search tree Also known as binary sort tree , Binary search tree satisfies All left child nodes are smaller than the value of their root node , All right child nodes are greater than the value of their root node , Every subtree on the binary search tree is a binary search tree , Therefore, the binary search tree can obtain an ordered sequence by traversing the middle order ( From small to large );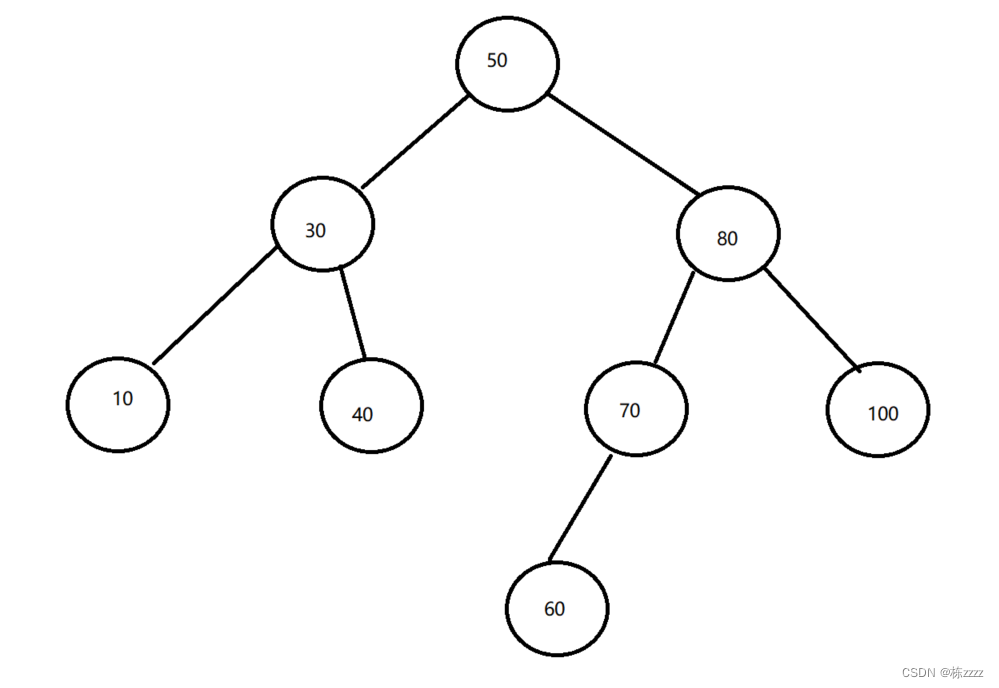

A tree like this is a binary search tree ;

2. Why introduced AVL Trees

Binary search tree looks beautiful , But it has some defects . For binary search tree , It is related to search , Whether it is to find or delete , You need to find it first , That is to traverse the whole tree , And yes n A binary search tree of nodes , If the probability of finding each element is equal , Then the average search length of the binary search tree is a function of the depth of the node in the binary search tree , That is, the deeper the node , The more times you compare . The optimal In the case of ： The binary search tree is a complete binary tree , The average number of comparisons is ：$lo{g}_{2}n$, But if the binary search tree degenerates into a single branch tree , The average number of comparisons is ：n/2, Namely The worst The situation of the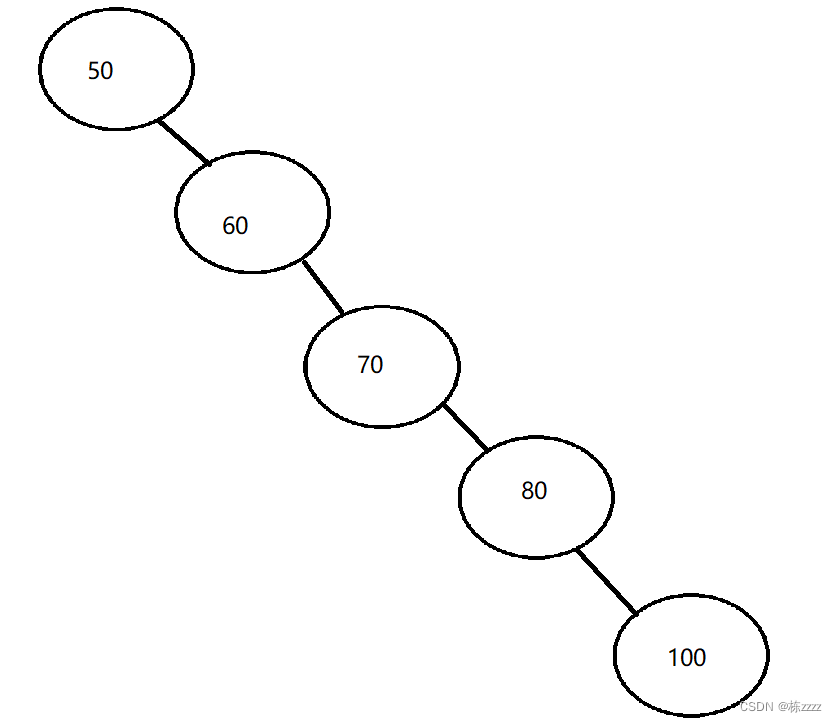

This is equivalent to the search of a sequential table , In this way, the advantage of binary search tree disappears completely , So it introduces AVL Trees !

3. What is? AVL Trees

AVL Tree is also called self balanced binary search tree , Is a highly balanced binary search tree , It is optimized on the basis of binary search tree , After inserting a new node into the binary search tree , Ensure that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1( You need to adjust the nodes in the tree ), That is to lower the height of the tree , This will reduce the average search length , therefore AVL The tree is satisfied Its left and right subtrees are AVL Trees , The difference between the height of the left and right subtrees ( It's called equilibrium factor ) The absolute value of is not more than 1(-1/0/1), This is it. AVL The advantage of trees , So if a binary search tree is highly balanced , It is AVL Trees . If it has n Nodes , Its height can be maintained at , Search time complexity O($lo{g}_{2}n$)!!!

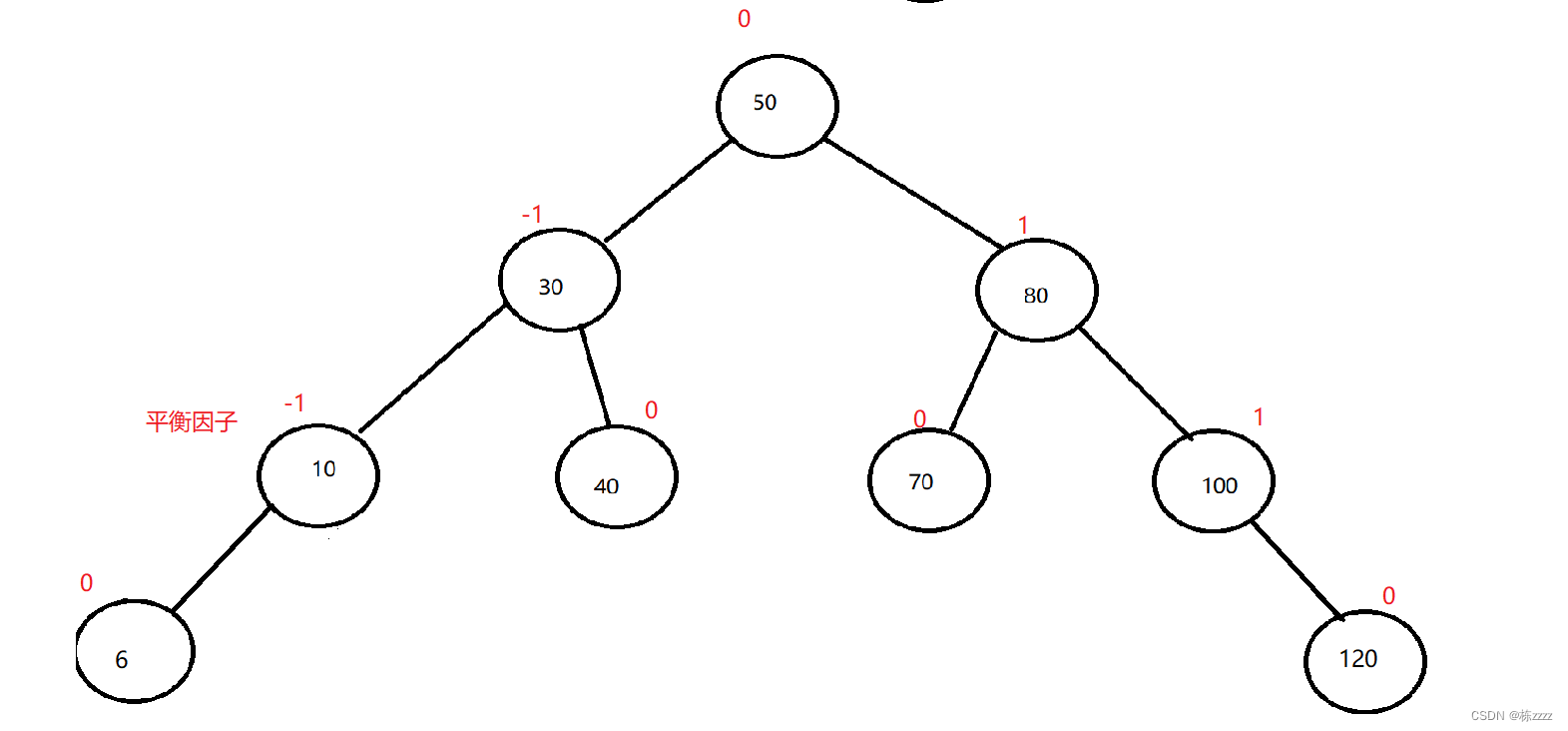
Balance factor = The height of the right subtree - The height of the left subtree

---

Two . Build your own AVL Trees

The structure here is similar to that of binary search tree , But if you insert elements here, you need to consider the balance factor , Because you must ensure that the tree is still a tree after inserting elements AVL Trees , Relevant adjustments are needed , Let's not introduce more here , Let's talk about it in detail , First, construct a simple AVL Trees ：

public class AVLTree {
    
    static class TreeNode{
    
        // Inner class , Express AVL Each node of the tree 

        //val value 
        public int val;
        // Left child's quote 
        public TreeNode left;
        // Right child's quote 
        public TreeNode right;
        // Reference of parent node 
        public TreeNode parent;
        // Balance factor ( Every node has ）
        public int bf;
        public TreeNode(int val){
    
            this.val = val;
        }
    }

    // The root node 
    public TreeNode root;
    public boolean insert(int val){
    
       
    }
}

Such a simple tree AVL The tree is constructed , Now let's write AVL Insertion of trees ！

---

3、 ... and .AVL Insertion and deletion of trees

1. Insert

First, insert the node , Like a binary search tree , First, just look at the location , Do not pay attention to the balance factor

This is the node to be inserted ：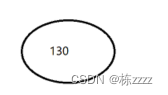

   TreeNode node = new TreeNode(val);
        if(root == null){
    
            // No root node , What you want to insert is the root node 
            root = node;
            return true;
        }
        // Record the parent node of each node 
        TreeNode parent = null;
        // Generation node to be moved 
        TreeNode cur = root;
        // according to val The value of and root Compare to determine where the node should be inserted 
        while (cur != null){
    
            if(cur.val > val){
    
                // Greater than proves that this node should be in the left subtree 
                parent = cur;
                cur = cur.left;
            }else if(cur.val < val){
    
                // Greater than proves that this node should be in the right subtree 
                parent = cur;
                cur = cur.right;
            }else {
    
                // You cannot have nodes with the same value 
                return false;
            }
        }
        // here cur It's empty , You need to find the corresponding location 
        if(parent.val > val){
    
            parent.left = node;
        }else{
    
            parent.right = node;
        }

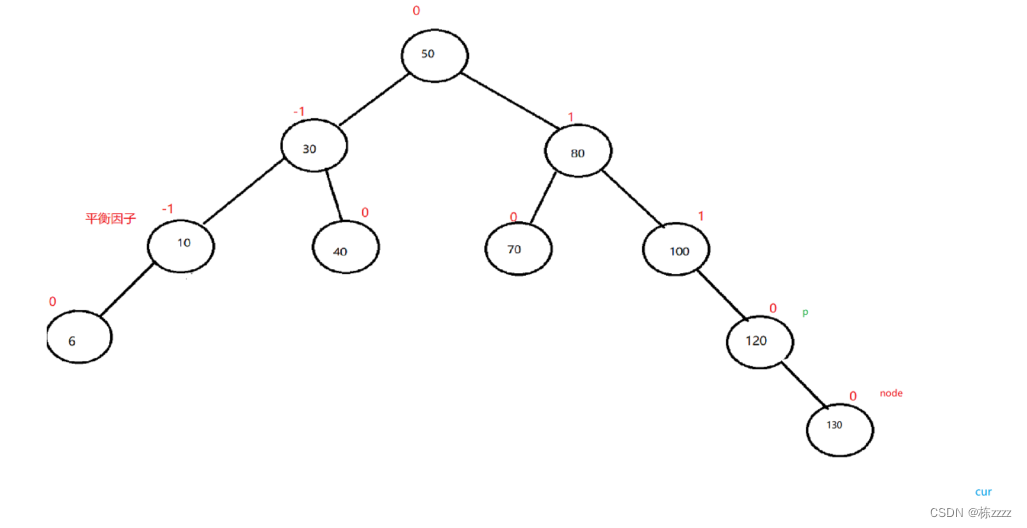
At this point, the node has been inserted , At this point, we need to look at the balance factor of each node

        // At this time, it is necessary to adjust the balance factor of the tree , Make sure the tree is highly balanced 
        // Then go back and write 
        node.parent = parent;
        cur = node;
        // When the parent node always exists , It means that you need to continue to adjust if you do not adjust to the root node 
        while(parent != null){
    
            if(cur == parent.right){
    
                // Add one to the height of the right tree on the right , therefore bf+1
                parent.bf++;
            }else{
    
                // To the left , Add one to the height of the left tree , therefore bf-1
                parent.bf--;
            }
            // Here is the judgment , If the balance factor of the parent node at this time is 0 了 , Then there is no need to go up , Because the above is balanced 
	        if(parent.bf == 0){
    
	            return true;
	        }else if(parent.bf == -1 || parent.bf == 1){
    
	            // At this time, the balance factor of the parent node is 1、-1
	             // This indicates that the current tree is balanced , But it doesn't mean that the whole tree is balanced , Therefore, we need to continue to go up 
	            cur = parent;
	            parent = cur.parent;
	        }else{
    
	            // At this time, the balance factor of the parent node is 2、-2
	            if(parent.bf == 2){
    
                // At this time, the right tree is tall   You need to lower the height of the right tree 
	                if(cur.bf == 1){
    
	                    // Left spin 
	                    rotateLeft(parent);
	                }else{
    
	                    // Right left double rotation 
	                    rotateRL(parent);
	                }
	            }else{
    
	                // At this time, the left tree is tall , You need to lower the height of the left tree 
	                if(cur.bf == 1){
    
	                    // Double left and right 
	                    rotateLR(parent);
	                }else{
    
	                    // Right single spin 
	                    rotateRight(parent);
	                }
	            }
	        }
        }

This is the current problem ：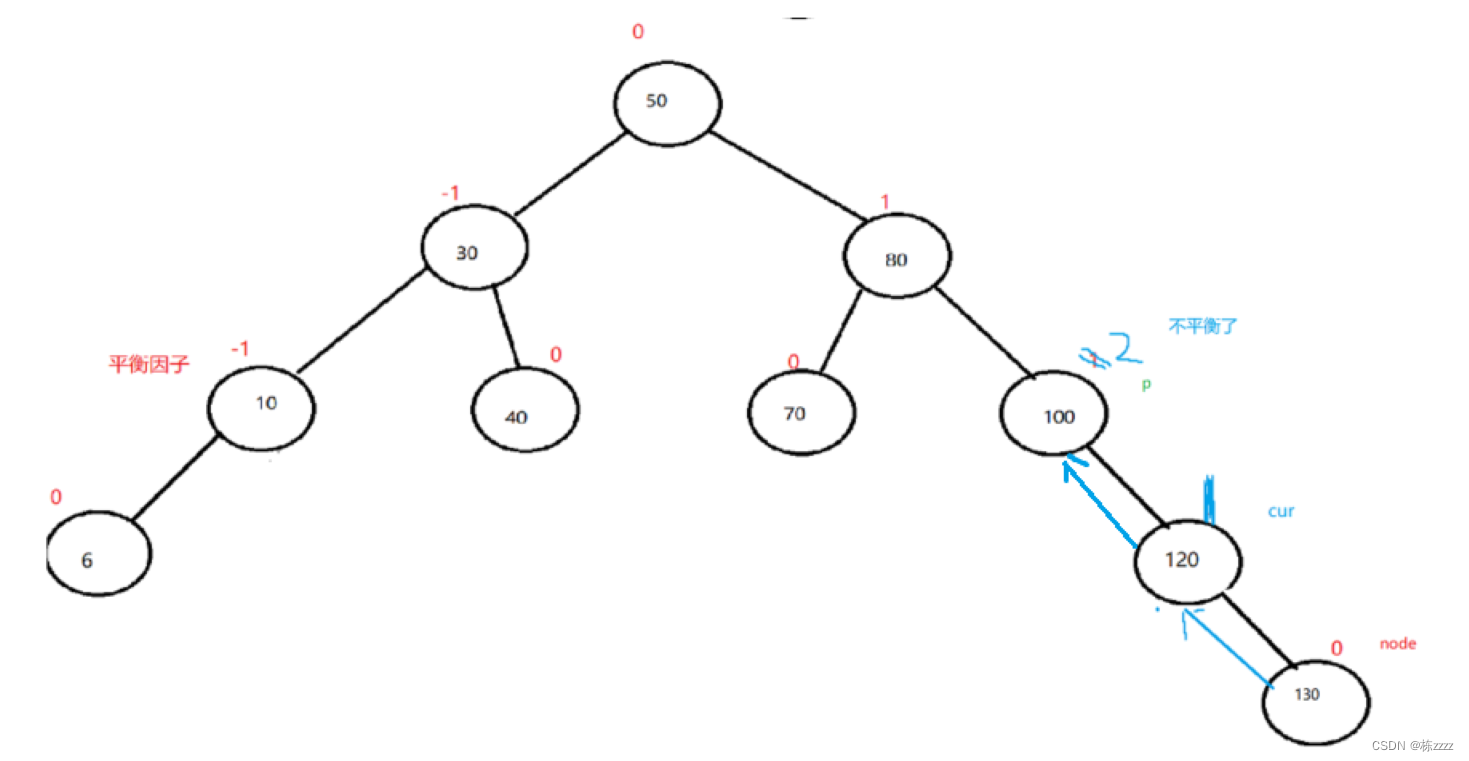

First, let's discuss some situations that will occur when adjusting the balance factor , Let's have a look at each of them ：
First, the balance factor is adjusted to 0 了 , Then there is no need to go up , Because the above is balanced , Of the current parent node The equilibrium factor is 0 It means that the inserted element only affects this tree , The above has no effect , So it is 0 Then it's over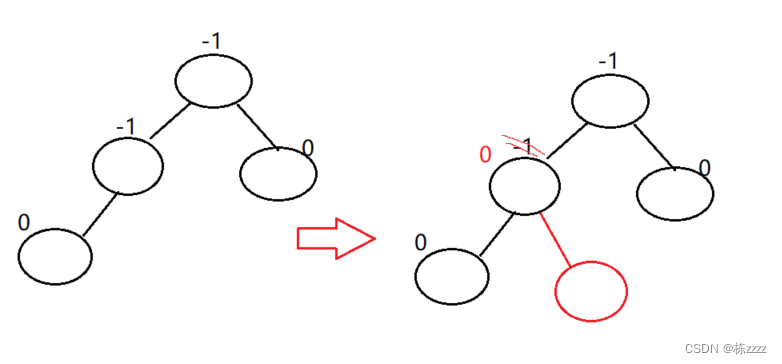

So it is 0 It means that the current is over , There's no need to go up , Others become 0 The situation is the same here is not detailed painting
And if it is 1 perhaps -1 Words , Indicates that the current tree is balanced , But it doesn't mean that the whole tree is balanced , So we need to go up again ;
And if it is 2 perhaps -2 Words , There are four situations , Let's take a look at them separately ：

1.1. Right single spin

here Zuo Shugao , You need to lower the height of the left tree , That is right-handed （parent.bf = -2,cur.bf = -1）：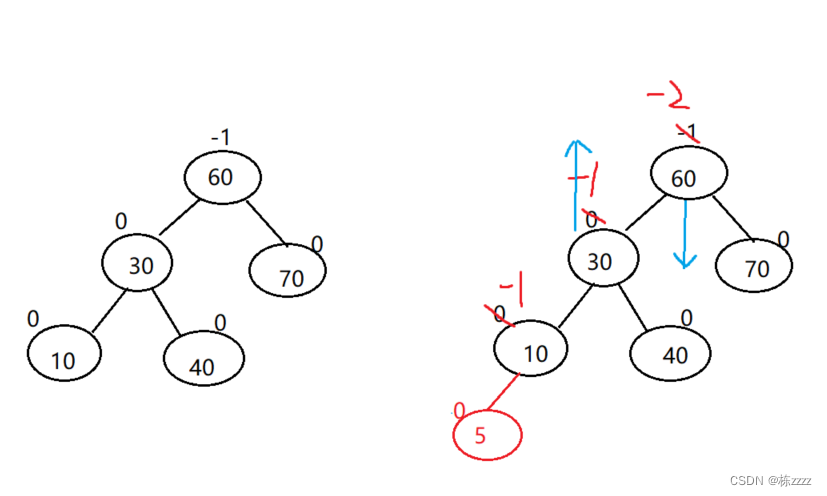

That is, the following effects ：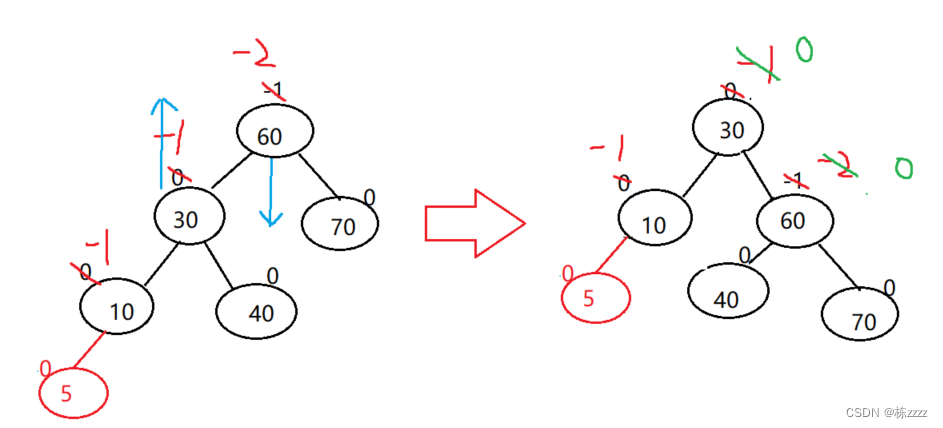

This is the adjustment process ：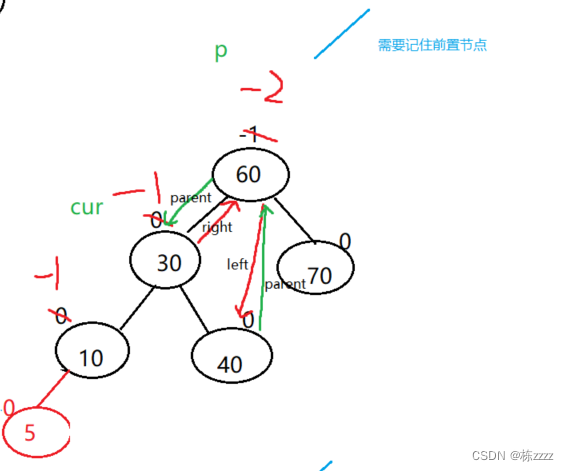

Write the code below ：

private void rotateRight(TreeNode parent){
    
        // Right single spin 
        // here parent The equilibrium factor of -2,cur The equilibrium factor of -1
        // Need record parent The root node 
        TreeNode pParent = parent.parent;

        TreeNode cur = parent.left;
        // Record cur The right of the node 
        TreeNode curR = cur.right;
        // If cur There is a right node that needs to be assigned to parent The left node , But if you don't have it, you don't need to give it 
        if(curR != null){
    
            parent.left = curR;
            curR.parent = parent;
        }
        // And then cur The right child of is changed to parent
        cur.right = parent;
        parent.parent = cur;

        // Check whether the current root node , It's not the root node, but the left subtree , Or right subtree 
        if(pParent != null){
    
            // Change the previous direction 
            cur.parent = pParent;
            if(parent == pParent.right){
    
                pParent.right = cur;
            }else{
    
                pParent.left = cur;
            }
        }else{
    
            // here parent Namely root, Because there is no root node 
            cur = root;
            root.parent = null;
        }

        // Finally, remember to modify the balance factor 
        parent.bf = 0;
        cur.bf = 0;
    }

Such a “ Simple ” The right single spin of is over ~

1.2. Left spin

This is the initial situation
here Right tree height , You need to lower the height of the right tree , That is left-handed （parent.bf = 2,cur.bf = 1）：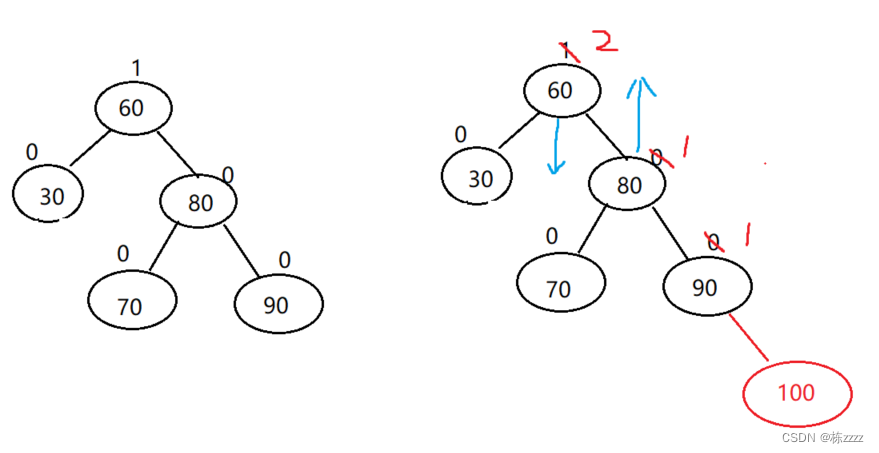

That is, the following effects ：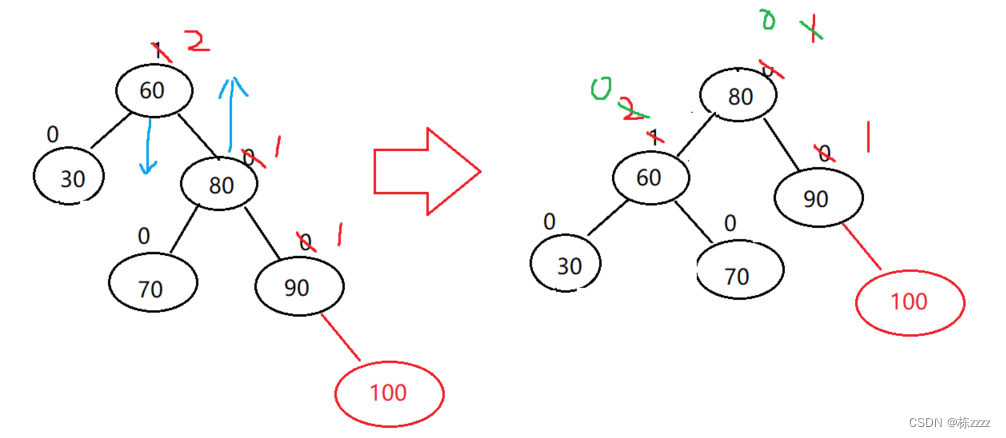

This is the adjustment process ：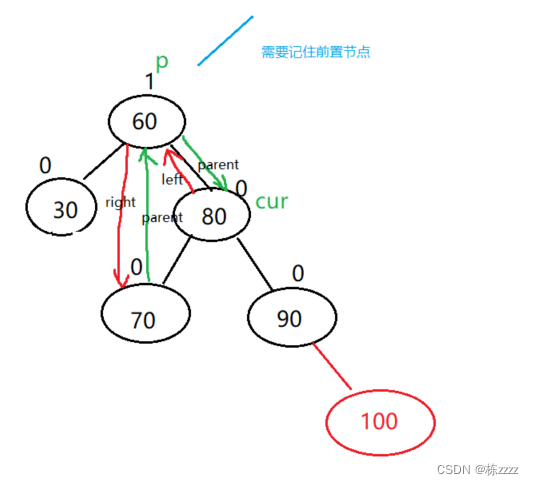

The code is as follows ：

private void rotateLeft(TreeNode parent){
    
        // Left spin 
        // here parent The equilibrium factor is 2,cur The equilibrium factor of 1
        // Parent node needs to be recorded 
        TreeNode pParent = parent.parent;

        TreeNode cur = parent.right;
        // Record cur The left node 
        TreeNode curL = cur.left;
        // Judge whether the left node is empty , If it is empty, there is no need to care , If it is not empty, you need to parent The right node points to it , And its parent node is parent
        if(curL != null){
    
            // Change direction 
            parent.right = curL;
            curL.parent = parent;
        }
        // change cur The direction of 
        cur.left = parent;
        parent.parent = cur;
        // Determine if the pParent Not empty , It means parent No root, It depends on whether it is a left child or a right child 
        if(pParent != null){
    
            cur.parent = pParent;
            if(parent == pParent.right){
    
                pParent.right = cur;
                
            }else{
    
                pParent.left = cur;
            }
        }else{
    
            // Root node 
            cur = root;
            root.parent = null;
        }
        cur.bf = 0;
        parent.bf = 0;
    }

Such a “ Simple ” The left single spin of is over ~

1.3. Double left and right

At this time, the left tree is tall , You need to lower the height of the left tree ,（parent.bf = -2,cur.bf = 1）：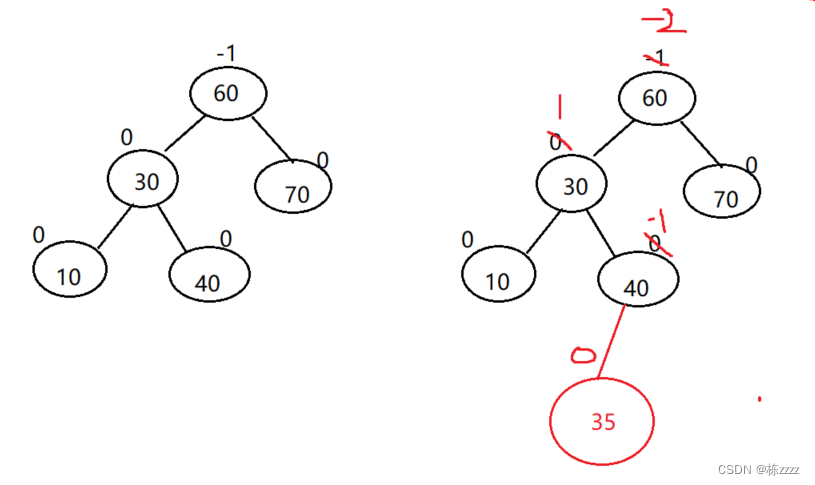

At this time, it is impossible to complete by single rotation , Need to pass through Two rotations To complete ：

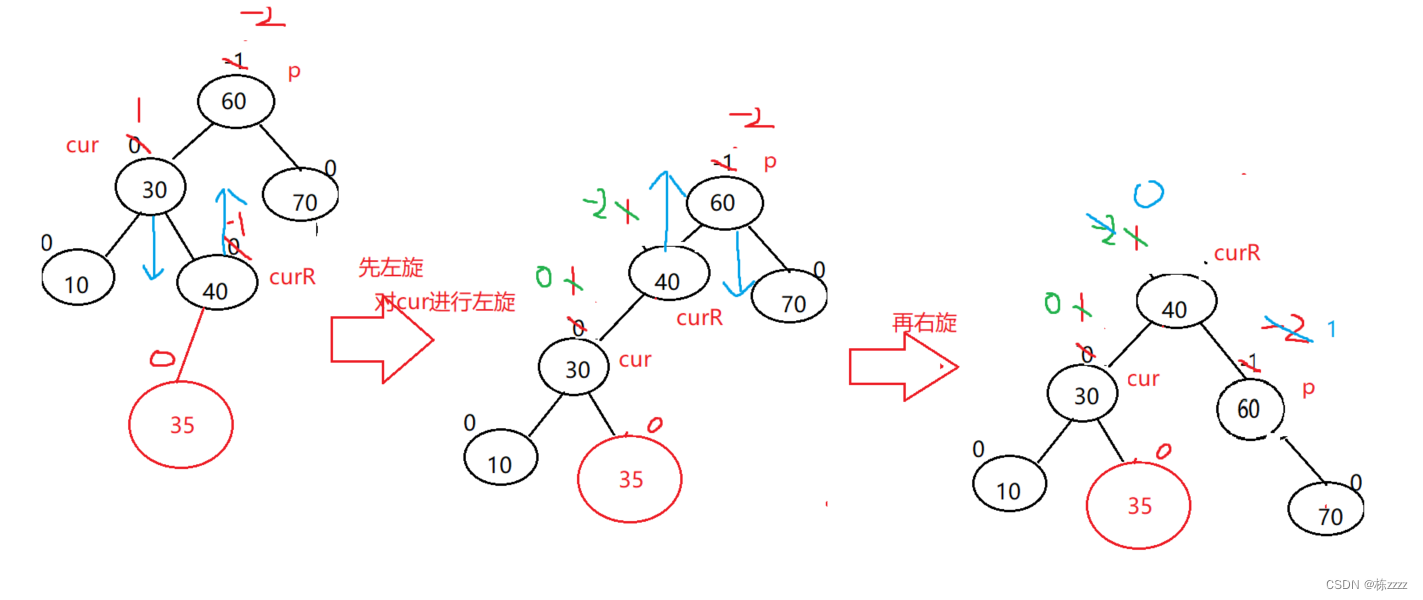
The left and right single spins have been introduced above , I won't go into details here ,
First left ：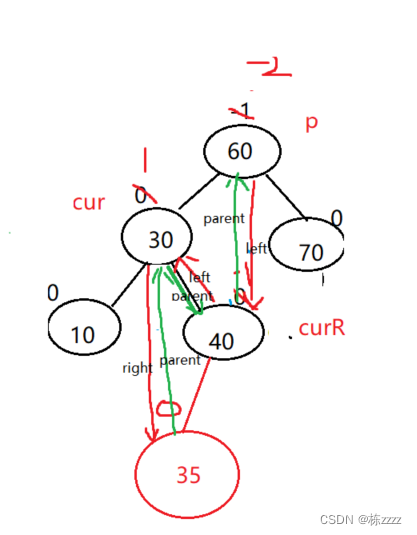

At this time, the modified balance factor is useless
Turn right again ：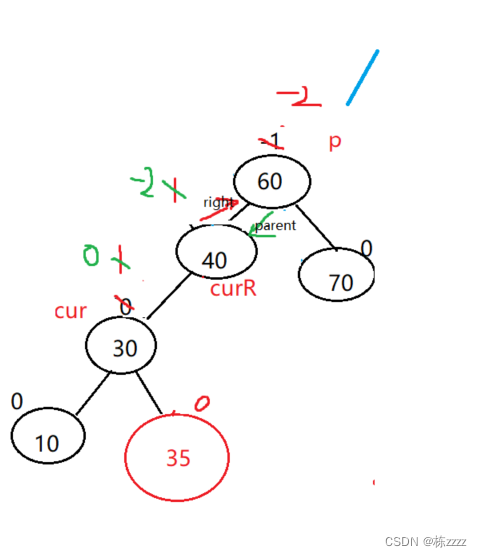

After two rotations, only Change the balance factor That's all right. ,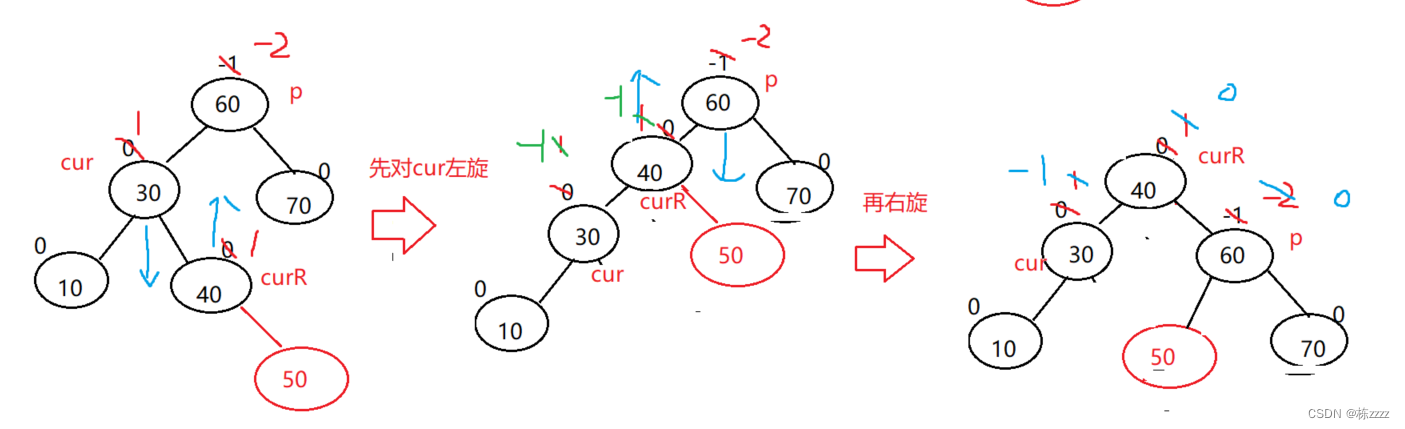

Through observation curR The equilibrium factor of , Will determine the balance factor of the last other nodes

The code is as follows ：

private void rotateLR(TreeNode parent){
    
        // Double left and right 
        TreeNode cur = parent.left;
        TreeNode curR = cur.right;
        // You need to see it now curR The equilibrium factor of , Then determine the balance factor of other nodes 
        int bf = curR.bf;
        // Call left rotation first, then right rotation 
        rotateLeft(parent.left);
        rotateRight(parent);
        if(bf == -1){
    
            curR.bf = 0;
            cur.bf = 0;
            parent.bf = 1;
        }else if(bf == 1){
    
            curR.bf = -1;
            cur.bf = 0;
            parent.bf = 0;
        }
    }

Such a left-right double rotation is over ~

1.4. Right left double rotation

At this time, the right tree is tall , You need to lower the height of the right tree （parent.bf = 2,cur.bf = -1）：

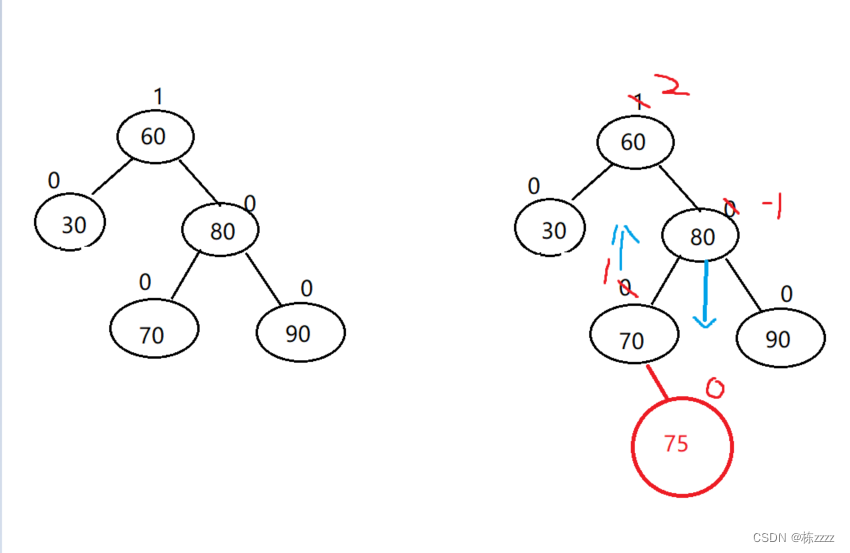
At this time, it is impossible to complete by single rotation , Need to pass through Two rotations To complete ：

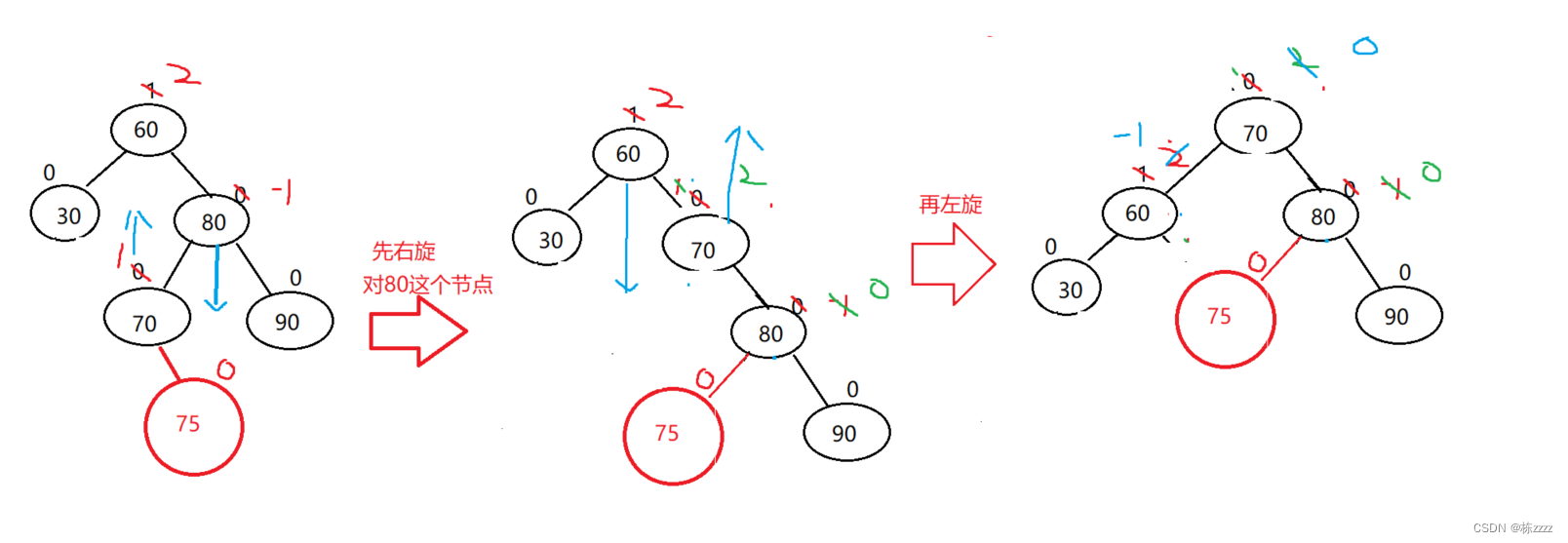
First right ：

Turn left again ：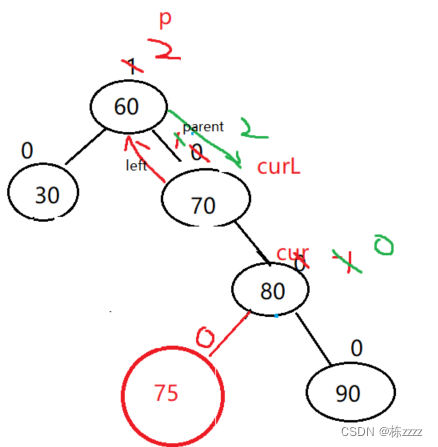

Through observation, it is found that the balance factor and curL It matters ：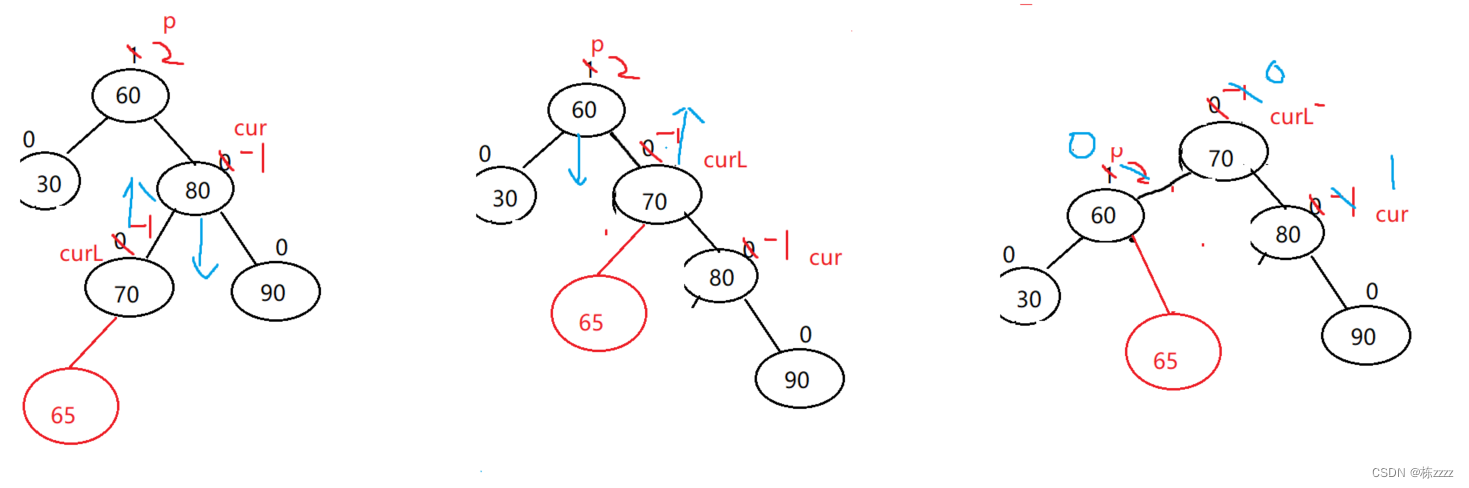

therefore
The code is as follows ：

 private void rotateRL(TreeNode parent) {
    
        // Right left double rotation 
        TreeNode cur = parent.right;
        TreeNode curL = cur.left;
        // You need to see it now curL The equilibrium factor of , Then determine the balance factor of other nodes 
        int bf = curL.bf;
        rotateRight(cur);
        rotateLeft(parent);

        if(bf == -1){
    
            cur.bf = 1;
            parent.bf = 0;
            curL.bf = 0;
        }else if(bf == 1){
    
            parent.bf = -1;
            curL.bf = 0;
            cur.bf = 0;
        }
    }

2. Delete

The deletion is similar to the insertion above , because AVL The tree is also a binary search tree , Nodes can be deleted in the form of binary search tree , Then update the balance factor , Just different from deletion , Balance factor update after node deletion , In the worst case, always adjust to the position of the root node .
Specific steps ：

1. Find the node to delete
2. Delete nodes according to the deletion rules of the search tree
3. Update equilibrium factor , If there is an imbalance , Rotate .– The single spiral , Twin twist

I won't write complete code here ！！

---

Come here ,AVL The introduction of the tree is over , We will continue to introduce red and black trees later ！！！