[CCPC] 2020ccpc Changchun F - band memory | tree heuristic merge (DSU on a tree), chairman tree

Want to make APP Same thing as WeChat , Can run small programs smoothly ？ | Experience will send you to Xinjiang 、 Huawei 、 Cherry keyboard ！>>>

Everyone will dsu The competition area of .. I had known that I would have opened the array a little bit ..

Bad 20 It's silver in minutes ..

The last one ccpc I'm sorry ...

The main idea of the topic ：

Give a tree

Let's find out ：

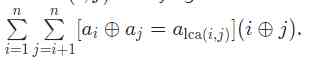
Topic ideas ：

notice lca, That would be to enumerate each point as lca The contribution of

So enumerate the current node as lca when , So what can contribute is , The contribution of any two of his subtrees

So directly enumerate all the points of the current subtree , And then match it with the previous weights

Here we need to split it bit by bit ：

a^(b+c) != a^b + a^c

But after dividing the number into bits , For the present lca Weight is ai = c, The current point is ak = a, For all previous weights in the subtree a^c The point of , If k Of the x Is it 1, Then take a look at a^c In the point of How many are in the first k Is it 0, vice versa

In this way, the contribution can be calculated

At this point, an operation is needed ：

The weight is calculated as c Of the k position yes 1 The number of

This place seems to work unorder_map perhaps multiset Get rid of it

But it's too safe to play ... Added chairman tree ..( It may not be safe Different results )

As for the heuristic merging here, it is nothing more than the principle of Huffman tree :

Let the subtree with the largest number of nodes visit only once , But here's a point , If the given tree is a chain , It's still going to get stuck n^2/2, But you need to pay attention to one detail ： There can be no ai = ai^aj The situation of , because aj Must be greater than 0

So at this point, you can directly exclude the chain of the case, the complexity of Overall control to O(nlogn)

After adding a chairman tree, the overall complexity is ：O(nlog^n)

Code:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5+6;
const int mod = 1e9+7;
const ll base = 1e9;
ll n,m,p;
ll a[maxn];
int L[maxn],R[maxn];
int cnt = 0;
vector<int>v[maxn];
vector< pair<int,int> >g[maxn];
struct node{
    int v[22],w;/// The first k Number of bits 
    int l,r;
}t[maxn*21];
int root[maxn];
int sz[maxn];
int cot = 0;
void Insert(int &x,int y,int l,int r,int pos,ll w){
    x = ++cnt;
    t[x] = t[y];
    for(int i=0;i<=20;i++)
        if(w>>i&1) t[x].v[i]++;
    t[x].w ++;
    if(l == r) return ;
    int mid = (l+r)/2;
    if(pos<=mid) Insert(t[x].l,t[y].l,l,mid,pos,w);
    else Insert(t[x].r,t[y].r,mid+1,r,pos,w);
}
ll Query(int x,int y,int l,int r,int pos,ll w){
    if(l == r){
        ll ans = 0;
        for(int i=0;i<=20;i++){
            if(w>>i&1)
                ans += ( (t[y].w - t[x].w) - (t[y].v[i]-t[x].v[i]) )*(1<<i);
            else
                ans += (t[y].v[i] - t[x].v[i])*(1ll<<i);
        }
        return ans;
    }
    int mid = (l+r)/2;
    if(pos <= mid) return Query(t[x].l,t[y].l,l,mid,pos,w);
    return Query(t[x].r,t[y].r,mid+1,r,pos,w);
}

void dfs(int u,int fa){
    sz[u] = 1;
    for(int e:v[u]){
        if(e == fa) continue;
        dfs(e,u);
        g[u].push_back({sz[e],e});
        sz[u] += sz[e];
    }
    sort(g[u].begin(),g[u].end());
}

void dfs1(int u){
    int sz = g[u].size();
    L[u] = ++cot;
    Insert(root[cot],root[cot-1],0,1e6,a[u],u);
    for(int i=sz-1;i>=0;i--){
        int e = g[u][i].second;
        dfs1(e);
    }
    R[u] = cot;
}

ll res = 0;
ll work(int u,int R,int L,int x){
    ll temp = 0;
    if(a[u]^x||a[u]^x<=1e6)
        temp += Query(root[L-1],root[R],0,1e6,a[u]^x,u);
    for(auto tempx:g[u])  temp += work(tempx.second,R,L,x);
    return temp;
}

void dfs2(int u){
    int sz = g[u].size();
    int pre = L[u],last = R[u];
    for(int i=sz-2;i>=0;i--){
        last = R[g[u][i+1].second];
        res += work(g[u][i].second,last,pre,a[u]);
    }
    for(int i=sz-1;i>=0;i--) dfs2(g[u][i].second);
}
int main(){

    scanf("%lld",&n);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    for(int i=1;i<=n-1;i++){
        int x,y;scanf("%d%d",&x,&y);
        v[x].push_back(y);
        v[y].push_back(x);
    }

    dfs(1,1);
    dfs1(1);
    dfs2(1);
    printf("%lld\n",res);
    return 0;
}
/**
6
4 2 1 6 6 5
1 2
2 3
1 4
4 5
4 6
**/