Evaluation multipath weswood congestion control on ns3

 A coupled form westwood congestion cotrol algorithm is proposed in [1], in order to gain better performance in wirelss network. The rule to adjust congestion window is given in [2] with a clear statement.
$$w_r\leftarrow \{\begin{array}{ll}{w}_r+\frac{\theta }{w_r},& \text{when an ack is received}\\ & \\ B_r\ast RT{T}_{min,r}& \text{when packet loss event happens}\end{array}\text{\hspace{1em}(1)}$$
 Here $\theta =\frac{\max B_r^2}{(\sum B_i{)}^2}$.
 A dumbbell topology is built to evaluate it performance.

/** Network topology
 *
 *    100Mb/s, 20ms                            100Mb/s, 20ms
 * n0--------------|                    |---------------n4
 *                 |   5Mbps/s, 10ms    |
 *                 n2------------------n3
 *  100Mb/s, 20ms  |                    |    100Mb/s, 20ms
 * n1--------------|                    |---------------n5
 *
 *
 */
n0--L0--n2--L1--n3--L2--n4
n1--L3--n2--L1--n3--L4--n5

 Four flows are tested.

Test1

flow1 and flow4 are two subflows of a multipath session. flow2 and flow3 take Reno for rate control. flow1 and flow2 take route(n0->n4). flow3 and flow4 take route(n1->n5).
 The sending rate of each flow: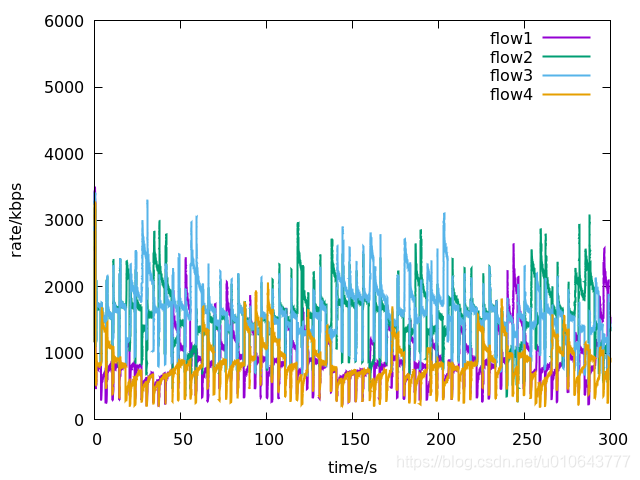

 Packets received rate, here mp denotes the total throughput of the multipath session: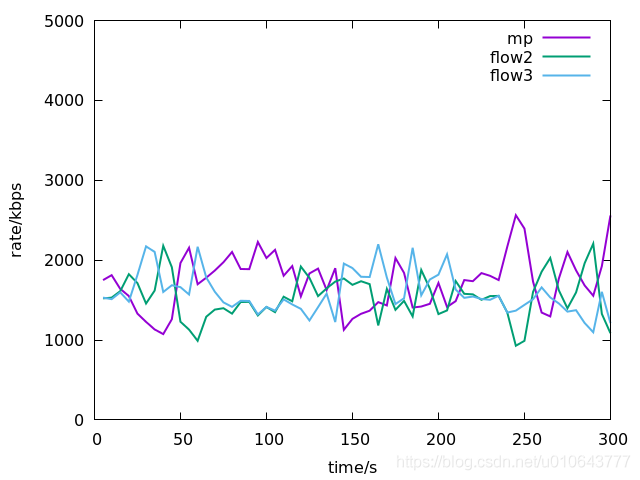

 The multipath westwood session can maintain well fairness to the two single path flows (flow2 and flow3).

Test2

 flow2 and flow3 take westwood for rate control. And the four flows are entering into network at different time.
 Packets received rate of each session: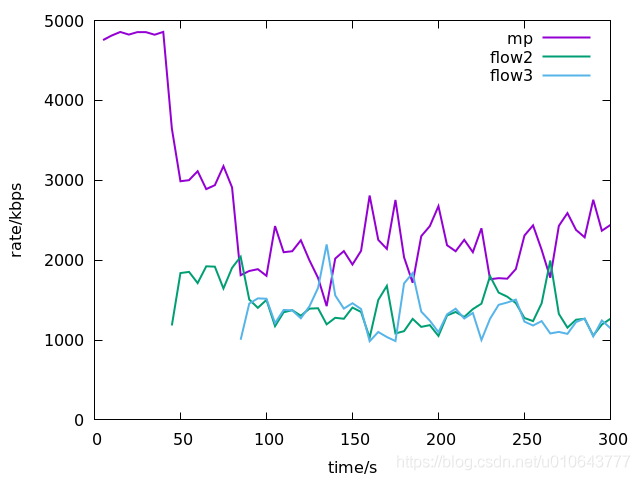

Why multipath westwood can maintain bottleneck fairness

 When a flow take westwood as conestion control, the theory throughput of in a sinpath westwood can be got accrording to[4]:
$$T_{single}=\frac{1}{\sqrt{rtt\times (rtt-rt{t}_{min})}}\times \sqrt{\frac{(1-p)}{p}}=B_{best}$$
 When a subflow follows the congestion control rule in Equation (1), the theory throughput of in this subflow can be got:
$$T_{subflow,i}=\frac{1}{\sqrt{rtt\times (rtt-rt{t}_{min})}}\times \sqrt{\frac{\theta \times (1-p)}{p}}=B_i\times \sqrt{\theta }$$
 With n subflow, by assuming these paths have same rtt, the total throughput of mpwestwood is:
$$T=n\times T_{subflow}$$
When $\theta =\frac{\max B_r^2}{(\sum B_i{)}^2}$,$T_{multipath}=B_{best}$.
[1] Wireless Multi-path TCP Westwood+ Modification to Achieve Fairness in HSDPA
[2] Improving the Performance of Multipath Congestion Control over Wireless Networks
[3] Evaluate multipath BBR congestion control on ns3
[4] westwood拥塞控制仿真