当前位置:网站首页>第三十一章:二叉树的概念与性质
第三十一章:二叉树的概念与性质
2022-08-02 14:10:00 【WANGHAOXIN364】
前置知识:树的概念与性质
为了保证学习效果,请保证已经掌握前置知识之后,再来学习本章节!
每个结点最多只有两个子结点的有根树称为二叉树。常常对两个子结点的顺序加以区分,分别称之为左子结点和右子结点。大多数情况下, 二叉树 一词均指有根二叉树。
二叉树的性质比较丰富,本章节将介绍二叉树的性质。请熟记这些性质。

学习目标
- 熟练掌握二叉树的概念和各种性质
- 能够综合利用二叉树的各种性质解决一些二叉树中的问题
二叉树的概念
定义
简单地理解,满足以下两个条件的树就是二叉树:
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
- 本身是有序树,即左子树和右子树的顺序不能颠倒,即使只有一棵子树,也要区分是左子树还是右子树。

形态
注意:以下各种情况下,一棵树都是一棵二叉树!
- 没有结点的树也是一棵树,称为空树!
- 只有一个根结点也是一棵树;
- 只有左子树的二叉树也是二叉树;
- 只有右子树的二叉树也是二叉树;
- 既有左子树,又有右子树的二叉树是一棵二叉树;

几种特殊的二叉树
1 斜树
顾名思义,斜树一定是斜的,但是往哪边斜还是有讲究的。
① 所有节点都只有左子树的二叉树称为 左斜树。
② 所有节点都只有右子树的二叉树称为 右斜树。
③ 斜树的每一层都只有一个节点,节点的个数和二叉树的深度相同。

2 满二叉树
在一棵二叉树中,如果所有分支节点都存在左子树和右子树(度为 2),并且所有叶子节点都在同一层上,这样
的二叉树称为满二叉树。

3 完全二叉树
对一棵具有 nn 个节点的二叉树按层次序编号,如果编号为 i(1<i≤n)i(1<i≤n) 的节点与同样深度的满二叉树中编号
为 ii 的节点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
也可以这么去定义完全二叉树:如果二叉树中除了最下层,其他每层都饱满,最下层的结点都集中在该层最左边的若干位置上,则此二叉树被称为完全二叉树。

注意:
(1)满二叉树是完全二叉树,完全二叉树不一定是满二叉树!
(2)在满二叉树的最下层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
(3)在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
二叉树的性质
由于二叉树结构的优美性,因此具有很多很好的性质。
性质1. 若二叉树中,叶子结点数为 n_0n0,度为 2 的结点数为 n_2n2,则 n_0=n_2+1n0=n2+1。
这个性质表明,在二叉树中,叶子结点的个数与度为度为 1 的结点个数无关。
证明如下(选学):
(1)设度为 1 的结点数为 n_1n1,那么显然有 n=n_0+n_1+n_2n=n0+n1+n2。—— ①
(2)设有 ee 条边,那么显然有 e = n-1 = n_1+2n_2e=n−1=n1+2n2。(nn个结点的树有 n-1n−1 条边,每个度为 1 的结点下有 1 条边,度为 2 的结点下有 2 条边,叶子结点下没有边)—— ②
(3)联立上面两个等式,② 式减 ① 式,即可得到 n_0=n_2+1n0=n2+1
性质2. 二叉树第 ii 层上的结点数目最多为 2^{i-1}2i−1。(i≥1i≥1,根节点深度为 11)
- 证明:略。
性质3. 深度为 kk 的二叉树至多有 2^k-12k−1 个结点(k≥1k≥1,根节点深度为 11)。
- 证明:树的第一层有 1 个结点,第二层最多有 2 个结点,第三层最多 4 个结点,......,第 kk 层最多 2^{k-1}2k−1 个结点。所以最多结点数为 S=2^0+2^1+2^2+...+2^{k-1}=2^k-1S=20+21+22+...+2k−1=2k−1。
- 特别的,深度为 kk,且有 2^k-12k−1 个结点的二叉树就是 满二叉树。满二叉树的每一层的结点数都达到了最大结点数。
性质4. 具有 nn 个结点的完全二叉树的深度为 \lfloor \log_2 (n) + 1 \rfloor⌊log2(n)+1⌋。
性质5. 在完全二叉树中,若将结点从上往下,从左到右进行编号,编号 1 \sim n1∼n。那么对编号为 xx 的结点,则其父结点编号为 \lfloor x/2 \rfloor⌊x/2⌋ ,左孩子编号为 2x2x,右孩子编号为 2x+12x+1。左右孩子存在的前提是其对应的编号不超过完全二叉树结点数量 nn。父结点存在的前提是结点 xx 不是根结点。
| 根结点 | 父结点 | 当前结点 | 左子结点 | 右子结点 | 最后一个结点 | |
|---|---|---|---|---|---|---|
| 存在条件 | —— | x/2 > 0 | —— | 2*x <= n | 2*x + 1 <= n | —— |
| 编号 | 1 | x/2 | x | 2*x | 2*x + 1 | n |
练习题
- 一棵完全二叉树的节点总数为18,其叶节点数是多少?
- 二叉树第10层的节点数的最大数目是多少?
- 一棵深度为10的满二叉树,其节点数量是多少?
- 一棵n个节点的完全二叉树,则该二叉树的高度h为?
- 如果一棵二叉树有N个度为2的节点,M个度为1的节点,则该树的叶子个数为?
练习题答案
- 根据完全二叉树的定义和构成和性质 1,答案为 9
- 根据性质 2,答案为 2^{10-1}=512210−1=512
- 根据性质 3,答案为 1023
- 根据性质 4,答案为: \lfloor \log_2 (n) + 1 \rfloor⌊log2(n)+1⌋
- 根据性质 1, 答案为 N+1
边栏推荐
- Detailed introduction to drawing complex surfaces using the plot_surface command
- 为vscode配置clangd
- Based on the matrix calculation in the linear regression equation of the coefficient estimates
- SQL的通用语法和使用说明(图文)
- Win10电脑不能读取U盘怎么办?不识别U盘怎么解决?
- 如何用硬币模拟1/3的概率,以及任意概率?
- What should I do if I install a solid-state drive in Win10 and still have obvious lags?
- 队列与栈
- What are IPV4 and IPV6?
- LeetCode 2354. 优质数对的数目 二进制01表示和集合之间的转换
猜你喜欢
MATLAB drawing command fimplicit detailed introduction to drawing implicit function graphics
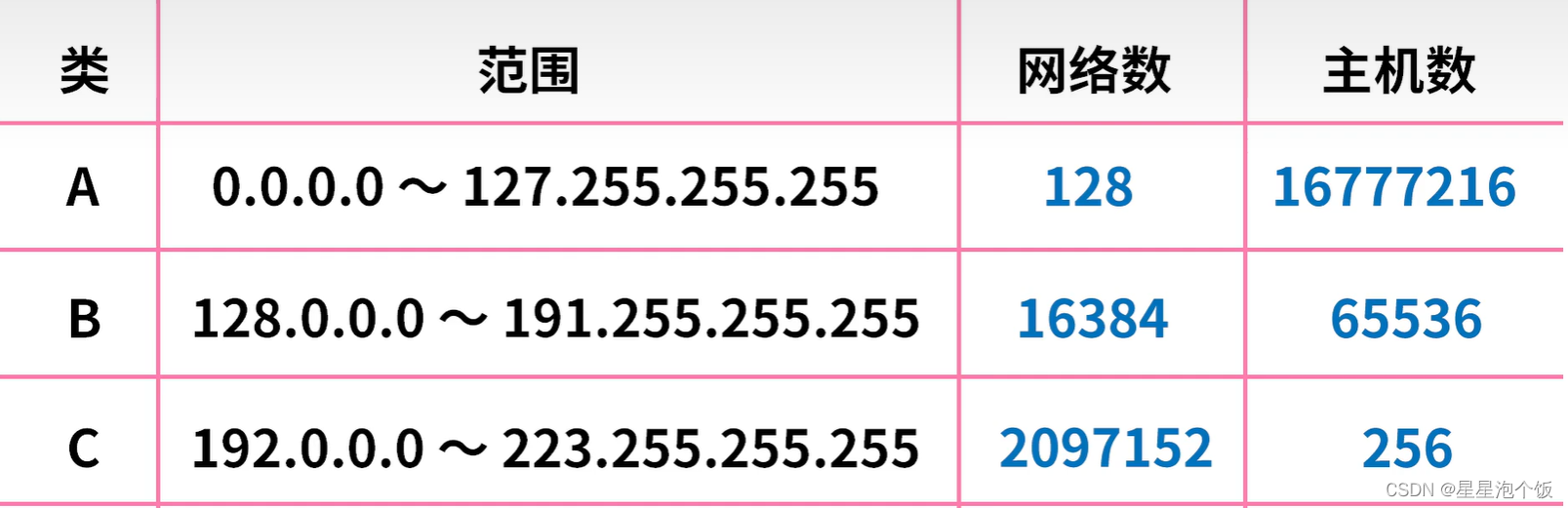
What are IPV4 and IPV6?
利用plot_surface命令绘制复杂曲面入门详解
1.开发社区首页,注册
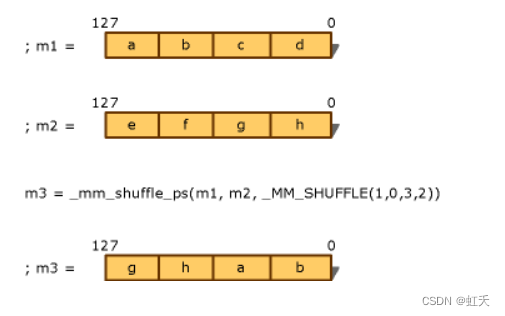
The SSE instructions into ARM NEON
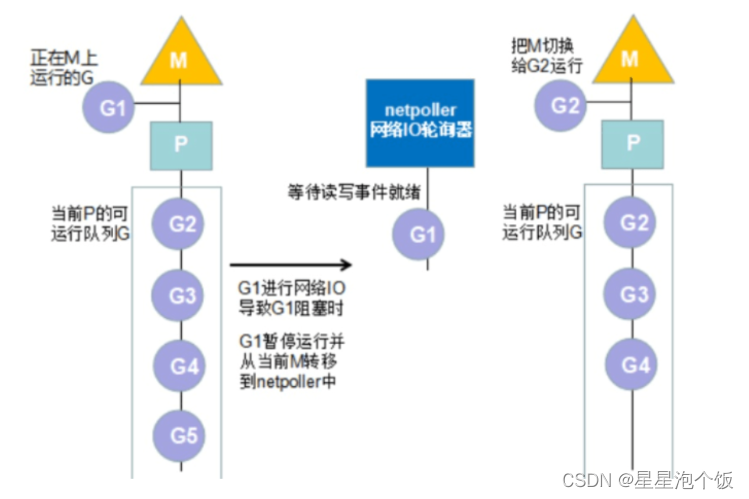
GMP scheduling model of golang
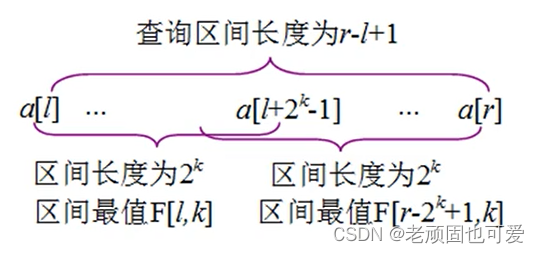
Doubled and sparse tables
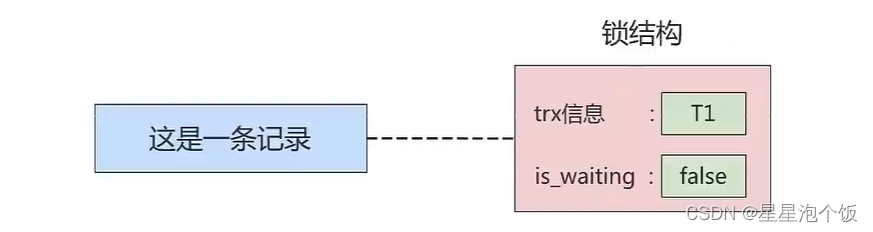
Mysql lock
What should I do if the Win10 system sets the application identity to automatically prompt for access denied?
奇技淫巧-位运算
随机推荐
Win10电脑需要安装杀毒软件吗?
Detailed explanation of Golang garbage collection mechanism
What is Win10 God Mode for?How to enable God Mode in Windows 10?
二叉排序树与 set、map
Win10电脑不能读取U盘怎么办?不识别U盘怎么解决?
Knapsack Problem - Dynamic Programming - Theory
Mysql连接错误解决
将SSE指令转换为ARM NEON指令
Installation and configuration of Spark and related ecological components - quick recall
5. Transaction management
win10 system update error code 0x80244022 how to do
Open the door of electricity "Circuit" (1): voltage, current, reference direction
Redis常见面试题
Failed to install using npx -p @storybook/cli sb init, build a dedicated storybook by hand
pygame图像连续旋转
深入理解Golang之Map
KiCad常用快捷键
推开机电的大门《电路》(二):功率计算与判断
win11一直弹出用户账户控制怎么解决
Win11 computer off for a period of time without operating network how to solve