当前位置:网站首页>第三十二章:二叉树的存储与遍历
第三十二章:二叉树的存储与遍历
2022-08-02 14:10:00 【WANGHAOXIN364】
前置知识:二叉树的概念与性质
为了保证学习效果,请保证已经掌握前置知识之后,再来学习本章节!
学习目标
熟练掌握二叉树的存储方式
理解二叉树的三种遍历方式的实现过程
给出一棵二叉树,能够写出对应的三种遍历序列,给出任意两种遍历序列,能够推导并还原出二叉树并写出另外一种遍历序列
掌握三种遍历方式的代码实现,掌握给出两种遍历方式的序列,求第三种遍历序列的代码实现
二叉树的存储
二叉树的存储和普通树基本一致。只是由于二叉树中的结点最多只有两个子节点,所以在存储子节点时有区别。
数组存储
Type val[N]; // 存当前结点的信息
int fa[N]; // 存父结点信息
int left[N], right[N]; // left[i],right[i]: 结点 i 的左孩子和右孩子编号
Copy
结构体存储
struct node{
Type val;
int fa;
int left, right;
} tree[N];
Copy
顺序存储
注意:顺序存储最适用于存储完全二叉树!
顺序存储采用数组下标去保存二叉树的结构,采用完全二叉树的编号方式存储二叉树。
根据二叉树的性质 5,可以快速定位结点 ii 的父结点( \lfloor i/2 \rfloor⌊i/2⌋),左孩子(2x2x),右孩子为(2x+12x+1)。
优点:存储方便,查找父结点、子节点方便
缺点: 除了完全二叉树之外,使用顺序存储会极大浪费空间

二叉树的遍历
树的遍历是指 从根节点出发,按照 某种次序 依次访问树中的所有结点,使得 每个结点都被访问仅被访问一次。
层次遍历
即广度优先遍历,遍历规则为:
若二叉树为空,则停止遍历并返回。
如果树不为空,则从根节点开始访问,从上而下逐层访问,在同一层中,按照左孩子、右孩子的顺序对节点逐个访问。

示例代码:
const int N = 10005;
char val[N]; // 存当前结点的信息
int left[N], right[N]; // left[i],right[i]: 结点 i 的左孩子和右孩子编号
void bfs(int root)
{
queue<int> q;
q.push(root);
while(!q.empty())
{
int k = q.front(); q.pop();
cout << k << ' ';
if(left[k]) q.push(left[k]);
if(right[k]) q.push(right[k]);
}
}
Copy
先序遍历
又称先根遍历、前序遍历。对于一棵非空的树,是指这样的一种遍历顺序:
- 访问根节点;
- 如果左子树不是空的,那么按照先序遍历的顺序遍历左子树;
- 如果右子树不是空的,那么按照先序遍历的顺序遍历右子树;

先序遍历可以总结成三个字: 根左右。容易看出,这种遍历方式的定义是一种递归定义的方式。因此,在代码实现上,先序遍历也是采用递归来实现的。示例代码如下:
// 结构体存树
struct node{
char val;
int left, right;
} t[N];
void visit(int node)
{
cout << t[root].val; // 输出当前结点——子树的根结点
}
void pre_order(int root)
{
visit(root); // 访问根节点
if(t[root].left)
pre_order(t[root].left); // 左子树不空,遍历左子树
if(t[root].right)
pre_order(t[root].right); // 右子树不空,遍历右子树
}
Copy
中序遍历
又称中根遍历。对于一棵非空的树,是指这样的一种遍历顺序:
- 如果根节点的左子树不是空的,那么按照中序遍历的顺序遍历左子树;
- 访问根节点;
- 如果根节点的右子树不是空的,那么按照中序遍历的顺序遍历右子树;

中序遍历可以总结成三个字: 左根右。容易看出,它和先序遍历一样都是递归定义,且只是遍历的顺序不同。示例代码如下:
// 结构体存树
struct node{
char val;
int left, right;
} t[N];
void visit(int node)
{
cout << t[root].val; // 输出当前结点——子树的根结点
}
void in_order(int root)
{
if(t[root].left)
in_order(t[root].left); // 左子树不空,遍历左子树
visit(root); // 访问根节点
if(t[root].right)
in_order(t[root].right); // 右子树不空,遍历右子树
}
Copy
后序遍历
又称后根遍历。对于一棵非空的树,是指这样的一种遍历顺序:
- 如果根节点的左子树不是空的,那么按照后序遍历的顺序遍历左子树;
- 如果根节点的右子树不是空的,那么按照后序遍历的顺序遍历右子树;
- 访问根节点;

后序遍历可以总结成三个字: 左右根。容易看出,它和先序遍历一样都是递归定义,且只是遍历的顺序不同。示例代码如下:
// 结构体存树
struct node{
char val;
int left, right;
} t[N];
void visit(int node)
{
cout << t[root].val; // 输出当前结点——子树的根结点
}
void in_order(int root)
{
if(t[root].left)
in_order(t[root].left); // 左子树不空,遍历左子树
if(t[root].right)
in_order(t[root].right); // 右子树不空,遍历右子树
visit(root); // 访问根节点
}
Copy
练习题
边栏推荐
- 模板系列-二分
- Flink + sklearn - use JPMML implement flink deployment on machine learning model
- Win10上帝模式干嘛的?Win10怎么开启上帝模式?
- Summarize computer network super comprehensive test questions
- Detailed explanation of MATLAB drawing function plot
- KiCad常用快捷键
- Use tencent cloud builds a personal blog
- A clean start Windows 7?How to load only the basic service start Windows 7 system
- Win10 cannot directly use photo viewer to open the picture
- pygame绘制弧线
猜你喜欢
Win10上帝模式干嘛的?Win10怎么开启上帝模式?
Win10系统设置application identity自动提示拒绝访问怎么办
Win11 keeps popping up User Account Control how to fix it
MATLAB绘图命令fimplicit绘制隐函数图形入门详解
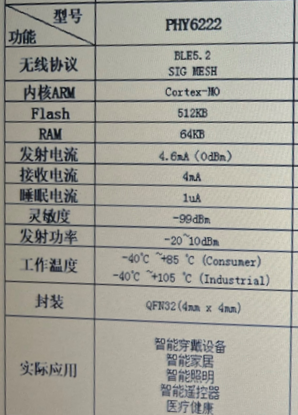
PHY6222蓝牙5.2支持MESH组网M0内核超低功耗
flink+sklearn——使用jpmml实现flink上的机器学习模型部署
动态规划理论篇
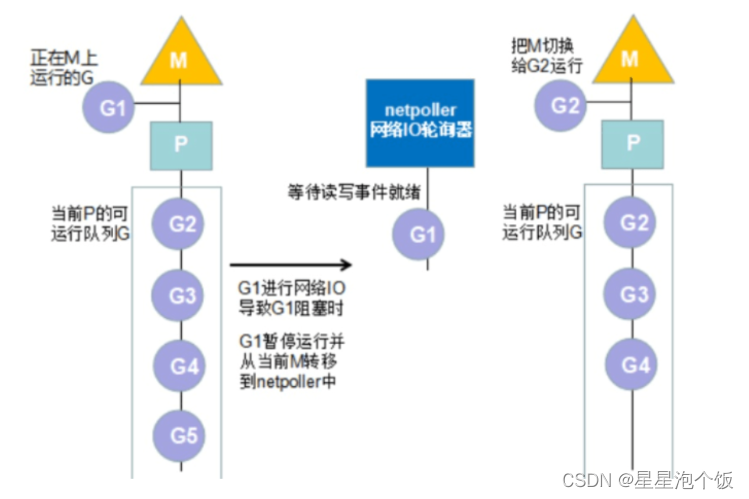
GMP scheduling model of golang
Do Windows 10 computers need antivirus software installed?
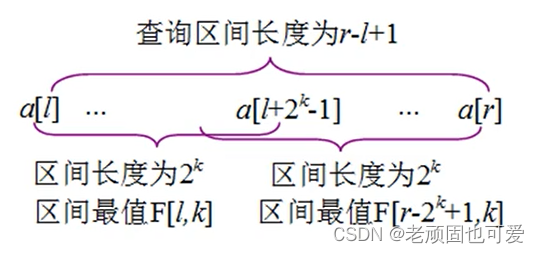
倍增和稀疏表
随机推荐
SQL的通用语法和使用说明(图文)
Publish module to NPM should be how to operate?Solutions to problems and mistake
使用 腾讯云搭建一个个人博客
Daily - Notes
2021-10-14
DP1101兼容CC1101是SUB1GHz无线收发芯片应用于智能家居
What should I do if Windows 10 cannot connect to the printer?Solutions for not using the printer
Win11电脑一段时间不操作就断网怎么解决
yolov5官方代码解读——前向传播
mysql的索引结构为什么选用B+树?
DP4301无线收发SUB-1G芯片兼容CC1101智能家居
How to reinstall Win7 system with U disk?How to reinstall win7 using u disk?
用U盘怎么重装Win7系统?如何使用u盘重装系统win7?
二叉树创建之层次法入门详解
What is Win10 God Mode for?How to enable God Mode in Windows 10?
基于矩阵计算的线性回归分析方程中系数的估计
推开机电的大门《电路》(一):电压,电流,参考方向
KiCad Common Shortcuts
一篇文章彻底理解Redis的持久化:RDB、AOF
Detailed explanation of Golang garbage collection mechanism
