当前位置:网站首页>[set theory] binary relationship (binary relationship notation | binary relationship from a to B | number of binary relationships | example of binary relationship)
[set theory] binary relationship (binary relationship notation | binary relationship from a to B | number of binary relationships | example of binary relationship)
2022-07-03 04:27:00 【Programmer community】
List of articles
- One 、 Binary relationship
- Two 、 Binary relation notation
- 3、 ... and 、 A To B The binary relationship of
- Four 、 A To B The number of binary relations
- 5、 ... and 、 A To B For example
One 、 Binary relationship
n
n
n Meta relationship :
Elements All are Orderly
n
n
n Set of tuples ;
n
n
n Meta relation example :
3 Meta relationship :
F
1
=
{
<
1
,
2
,
3
>
,
<
a
,
b
,
c
>
,
<
Count
learn
,
matter
The reason is
,
turn
learn
>
}
F_1 = \{ <1, 2, 3> , <a, b, c> , < mathematics , Physics , chemical > \}
F1={ <1,2,3>,<a,b,c>,< Count learn , matter The reason is , turn learn >}
F
1
F_1
F1 yes
3
3
3 Meta relationship , Each of its elements is Orderly
3
3
3 Tuples ;
4 Meta relationship :
F
2
=
{
<
1
,
2
,
3
,
4
>
,
<
a
,
b
,
c
,
d
>
,
<
language
writing
,
Count
learn
,
matter
The reason is
,
turn
learn
>
}
F_2 = \{ <1, 2, 3, 4> , <a, b, c, d> , < Chinese language and literature , mathematics , Physics , chemical > \}
F2={ <1,2,3,4>,<a,b,c,d>,< language writing , Count learn , matter The reason is , turn learn >}
F
2
F_2
F2 yes
4
4
4 Meta relationship , Each of its elements is Orderly
4
4
4 Tuples ;
Above order
n
n
n Tuples , The number is the same , The properties of elements can be different ;
Two 、 Binary relation notation
If
F
F
F It's a binary relationship (
F
F
F It's order
2
2
2 Tuple set )
Then there are :
<
x
,
y
>
∈
F
<x, y> \in F
<x,y>∈F
⇔
\Leftrightarrow
⇔
x
And
y
Yes
F
Turn off
system
x And y Yes F Relationship
x And y Yes F Turn off system
⇔
\Leftrightarrow
⇔
x
F
y
xFy
xFy
Binary relation notation :
① Infix notation ( infix ) :
x
F
y
xFy
xFy
② Prefix notation ( prefix ) :
F
(
x
,
y
)
F(x, y)
F(x,y) , or
F
x
y
Fxy
Fxy
③ Suffix notation ( suffix ) :
<
x
,
y
>
∈
F
<x,y> \in F
<x,y>∈F , or
x
y
F
xyF
xyF
Such as :
2
<
5
2 < 5
2<5 ,
2
2
2 Less than
5
5
5 ;
① Infix notation ( infix ) :
2
<
5
2 < 5
2<5
② Prefix notation ( prefix ) :
<
(
2
,
5
)
<(2, 5)
<(2,5)
③ Suffix notation ( suffix ) :
<
2
,
5
>
∈
<
<2,5> \in <
<2,5>∈<
3、 ... and 、 A To B The binary relationship of
A
A
A To
B
B
B The concept of binary relation :
A
×
B
A \times B
A×B Of Any subset yes
A
A
A To
B
B
B The binary relationship of
⇔
\Leftrightarrow
⇔
R
⊆
A
×
B
R \subseteq A \times B
R⊆A×B
⇔
\Leftrightarrow
⇔
R
∈
P
(
A
×
B
)
R \in P(A \times B)
R∈P(A×B)
A
A
A To
B
B
B The binary relationship of There may be
1
1
1 A collection of ,
2
2
2 A collection of ,
⋯
\cdots
⋯ ,
n
n
n A collection of ;
Four 、 A To B The number of binary relations
A
A
A To
B
B
B The number of binary relations :
∣
A
∣
=
m
|A| = m
∣A∣=m ,
∣
B
∣
=
n
|B| = n
∣B∣=n
A
A
A Number of collection elements
m
m
m individual ,
B
B
B Number of collection elements
n
n
n individual ;
Number of ordered pairs :
∣
A
×
B
∣
=
m
n
|A \times B| = mn
∣A×B∣=mn
Binary relationship Number :
∣
P
(
A
×
B
)
=
2
m
n
∣
|P(A \times B) = 2^{mn}|
∣P(A×B)=2mn∣, namely Above
m
n
mn
mn An ordered pair of total sets Power set Number ;
A
A
A To
B
B
B The number of binary relations =
A
×
B
A \times B
A×B Number of power sets =
2
m
n
2^{mn}
2mn individual
5、 ... and 、 A To B For example
A
=
{
a
1
,
a
2
}
A = \{a_1, a_2\}
A={ a1,a2} ,
B
=
{
b
}
B = \{ b \}
B={ b}
A
A
A aggregate And
B
B
B The Cartesian product of a set is :
A
×
B
=
{
∅
,
{
<
a
1
,
b
>
}
,
{
<
a
2
,
b
>
}
}
A \times B = \{ \varnothing, \{ <a_1 , b> \} , \{ <a_2 , b> \} \}
A×B={ ∅,{ <a1,b>},{ <a2,b>}}
analysis : Among them is
3
3
3 An orderly pair of , The number of binary relations is
2
2
×
1
=
4
2^{2 \times 1} = 4
22×1=4 individual , namely Above The power set of ordered pairs , Namely Yes
0
0
0 The number of ordered pairs
0
0
0 individual ,
1
1
1 The number of ordered pairs
2
2
2 individual ,
2
2
2 Number of ordered pairs
1
1
1 individual ;
A
A
A aggregate To
B
B
B A collection of Binary relationship : Yes
4
4
4 individual ;
R
1
=
∅
R_1 = \varnothing
R1=∅ ,
a
1
a_1
a1 And
b
b
b It doesn't matter. ,
a
2
a_2
a2 And
b
b
b It doesn't matter. ;
R
2
=
{
<
a
1
,
b
>
}
R_2 = \{ <a_1 , b> \}
R2={ <a1,b>} ,
a
1
a_1
a1 And
b
b
b It matters ,
a
2
a_2
a2 And
b
b
b It doesn't matter. ;
R
3
=
{
<
a
2
,
b
>
}
R_3 = \{ <a_2 , b> \}
R3={ <a2,b>} ,
a
1
a_1
a1 And
b
b
b It matters ,
a
2
a_2
a2 And
b
b
b It doesn't matter. ;
R
4
=
{
<
a
1
,
b
>
,
<
a
2
,
b
>
}
R_4 = \{ <a_1 , b> , <a_2, b> \}
R4={ <a1,b>,<a2,b>},
a
2
a_2
a2 And
b
b
b It matters ,
a
1
a_1
a1 And
b
b
b It matters ;
B
B
B aggregate And
A
A
A The Cartesian product of a set is :
A
×
B
=
{
∅
,
{
<
b
,
a
1
>
}
,
{
<
b
,
a
2
>
}
}
A \times B = \{ \varnothing, \{ <b, a_1 > \} , \{ <b, a_2 > \} \}
A×B={ ∅,{ <b,a1>},{ <b,a2>}}
analysis : Among them is
3
3
3 An orderly pair of , The number of binary relations is
2
2
×
1
=
4
2^{2 \times 1} = 4
22×1=4 individual , namely Above The power set of ordered pairs , Namely Yes
0
0
0 The number of ordered pairs
0
0
0 individual ,
1
1
1 The number of ordered pairs
2
2
2 individual ,
2
2
2 Number of ordered pairs
1
1
1 individual ;
B
B
B aggregate To
A
A
A A collection of Binary relationship : Yes
4
4
4 individual ;
R
5
=
∅
R_5 = \varnothing
R5=∅ ,
b
b
b And
a
1
a_1
a1 It doesn't matter. ,
b
b
b And
a
2
a_2
a2 It doesn't matter. ;
R
6
=
{
<
b
,
a
1
>
}
R_6 = \{ <b, a_1 > \}
R6={ <b,a1>} ,
b
b
b And
a
1
a_1
a1 It matters ,
b
b
b And
a
2
a_2
a2 It doesn't matter. ;
R
7
=
{
<
b
,
a
2
>
}
R_7 = \{ <b, a_2> \}
R7={ <b,a2>} ,
b
b
b And
a
1
a_1
a1 It doesn't matter. ,
b
b
b And
a
2
a_2
a2 It matters ;
R
8
=
{
<
b
,
a
1
>
,
<
b
,
a
2
>
}
R_8 = \{ <b, a_1 > , <b, a_2> \}
R8={ <b,a1>,<b,a2>} ,
b
b
b And
a
1
a_1
a1 It matters ,
b
b
b And
a
2
a_2
a2 It matters ;
边栏推荐
- Solve BP Chinese garbled code
- Library management system based on SSM
- Data Lake three swordsmen -- comparative analysis of delta, Hudi and iceberg
- Php+mysql registration landing page development complete code
- [Chongqing Guangdong education] reference materials for design and a better life of Zhongyuan Institute of science and technology
- How to choose cross-border e-commerce multi merchant system
- Basic MySQL operations
- The time has come for the domestic PC system to complete the closed loop and replace the American software and hardware system
- 金仓数据库KingbaseES 插件kdb_database_link
- 300+ documents! This article explains the latest progress of multimodal learning based on transformer
猜你喜欢

When using the benchmarksql tool to test the concurrency of kingbasees, there are sub threads that are not closed in time after the main process is killed successfully

拆一辆十万元的比亚迪“元”,快来看看里面的有哪些元器件。
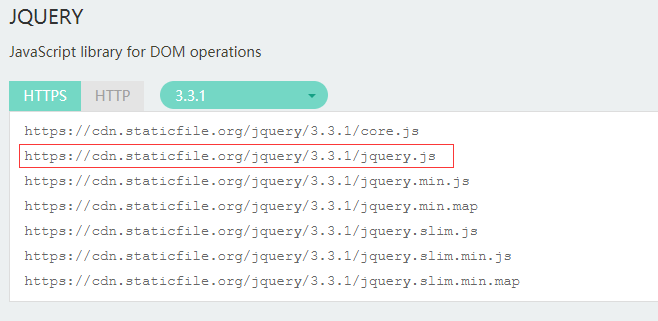
JS realizes lazy loading of pictures
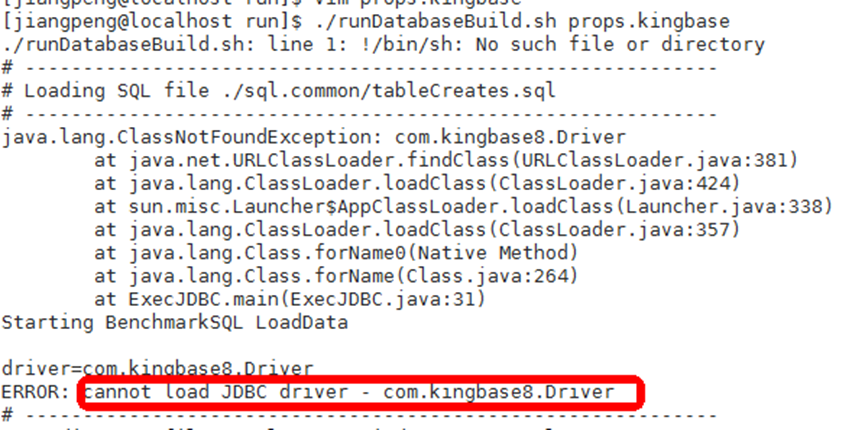
使用BENCHMARKSQL工具对kingbaseES执行灌数据提示无法找到JDBC driver

Supervised pre training! Another exploration of text generation!

P35-P41 fourth_ context

Jincang KFS data bidirectional synchronization scenario deployment
![[pat (basic level) practice] - [simple simulation] 1063 calculate the spectral radius](/img/01/c118725f74e39742df021b5dbcc33b.jpg)
[pat (basic level) practice] - [simple simulation] 1063 calculate the spectral radius
![[literature reading] sparse in deep learning: practicing and growth for effective information and training in NN](/img/7e/50fa6f65b5a4f0bb60909f57daff56.png)
[literature reading] sparse in deep learning: practicing and growth for effective information and training in NN
js实现在可视区内,文字图片动画效果
随机推荐
国产PC系统完成闭环,替代美国软硬件体系的时刻已经到来
使用BENCHMARKSQL工具对KingbaseES预热数据时执行:select sys_prewarm(‘NDX_OORDER_2 ‘)报错
Wine travel Jianghu War: Ctrip is strong, meituan is strong, and Tiktok is fighting
Solve BP Chinese garbled code
[set theory] set operation (Union | intersection | disjoint | relative complement | symmetric difference | absolute complement | generalized union | generalized intersection | set operation priority)
How to connect WiFi with raspberry pie
Js/ts bottom implementation double click event
BMZCTF simple_ pop
[set theory] Cartesian product (concept of Cartesian product | examples of Cartesian product | properties of Cartesian product | non commutativity | non associativity | distribution law | ordered pair
How to use kotlin to improve productivity: kotlin tips
mysql字段userid逗号分开保存按userid查询
Busycal latest Chinese version
js实现在可视区内,文字图片动画效果
[set theory] set identities (idempotent law | exchange law | combination law | distribution rate | De Morgan law | absorption rate | zero law | identity | exclusion law | contradiction law | complemen
AWS VPC
sd卡数据损坏怎么回事,sd卡数据损坏怎么恢复
Mila, University of Ottawa | molecular geometry pre training with Se (3) invariant denoising distance matching
PostgreSQL database high availability Patroni source code learning - etcd class
[software testing-6] & Test Management
Redraw and reflow