Gilbert Strang's course notes on linear algebra - Lesson 2

The topic of the second lesson is ： Matrix Elimination operation

---

example 1： Two ways of solving equations

Let's start with a question , Suppose we now have a system of equations ：

The first solution is ： take 1 Equation to y = 5 - 2x, Then substitute it into 2 Formula solution x Solution , And then you get y Solution . That is, through " use x To express y" In order to eliminate y

The second solution is ： take 1 The left and right of the equation are multiplied by 3 obtain ：6x + 3y = 15, then 2 Form and 1 Formula subtraction , obtain -y = -7, namely y = 7, Dai Huide x = -1. That is, through “ Operate on the equations ” Eliminate from a formula x

“ take 1 The left and right of the equation are multiplied by 3, And will 2 Form and 1 Formula subtraction ” The process of , In fact, that is Matrix elimination

When the unknowns become more , Method 1 Our thinking methods are often inefficient and disorderly , Using the appropriate elimination method will significantly improve the efficiency of the operation

---

example 2： The elimination process of ternary equations

Now let's use a system of three variable equations as an example to decompose the process of elimination ：

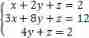
  For the convenience of expression , It can be written as Ax = b In the form of ：

Write it as Ax = b In the form of ：

  The first step of elimination , In fact, it is to eliminate the first unknown , Here it is. x

The operation steps are: ： Put the equation 1 in x The coefficient of is based on the following equation x Transform and subtract the corresponding coefficients

For example, in equation 2 in ,x The coefficient before is 3, So we'll have the equation 1 multiply 3, And then by the equation 2 Subtractive form 1, obtain ：

After calculation, we get ：

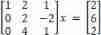
  here , Except for the first element, the first column is 0, It means that we have finished the x The elimination of element ！

And this 1 That's ok 1 The elements of the column "1" It can be called a ” Fulcrum ”（pivot）： The fulcrum is that we need to be based on it , Operate on it and its row （ Multiply ） Go down ” cater to ” In other formulas, the coefficients corresponding to the unknowns to be eliminated in this round are used to get the objective of elimination .

And the fulcrum cannot be 0（ Because it doesn't work 0 To eliminate other things ）

It's easy to say , Each step of elimination is to find the relationship downward based on the fulcrum , Then, according to the relation, the multiplication and subtraction are performed to complete the elimination , Then take down a fulcrum and continue the downward operation , Until it can no longer be eliminated .

Take the example above ,1 And 3 The relationship between 3 times , In order to 3 Elimination requires progressive 2 - ( type 1 * 3) The operation of

Now turn to the next parameter y The elimination of element ：

Let's get rid of the first line , take 2 That's ok 2 The elements of the column "2" It is called fulcrum , Use the second line to eliminate the third line , obtain ：

After calculation, we get ：

  here , The values below the fulcrum of the second column are 0, It means that we have finished the y The elimination of element ！ 

Yes x And y After the elimination , So the equation can be solved , At this point, we The elimination of the matrix is completed ！

Solve the equation after elimination ： from 5z = -10 Start to understand , Available z = -2, Replace the equation 2 Available y = 1, And then according to the equation 1 Available x = 2

The process of substituting into the solution is also called The process of retrogression （back substitution）

It needs to be mentioned that , In this case , Diagonal 1、2、5 All are fulcrum . Although the 5 There is no substantive operation , But if there is another line below ,5 Will become a fulcrum to eliminate the following Yuan , therefore 5 Belonging to a fulcrum in nature

Be careful , Elimination will also fail （ Causes the equation to be insoluble ）：

In the process of elimination, if one or more lines appear 0, This will make m An unknown number m The first equation becomes m The number of unknowns is less than m An equation , Causes the equation to be insoluble

---

example 3： How to explain matrix multiplication by row column combination ？

We have seen the process of matrix elimination , So how to express the operation process of matrix elimination ？

Let's review one thing first , Suppose there's an equation ：

  Turn into Ax = b In the form of ：

can Further written as ：

To understand from the perspective of columns is ：x The first column is related to y The second column can be combined to get the target vector

Now if I want to x Put it in A Left side , Then I will first perform an operation of left and right transposition of the equation （ Transpose related formulas ：） Other operations of attached matrix ：6.5 Matrix operation and its operation rules

  obtain

Explain in terms of vectors , We can say that the objective vector is composed of x individual And y individual Composed of

This is the same as before , It's just here in the behavioral dimension , Previously, columns were used as dimensions

What do you get from this example ： When x stay A On the right , Our interpretation of the results is based on A Of Column according to x Are combined ; When x stay A On the left , Our interpretation of the results is based on A Of That's ok according to x Are combined

If it is x Is not a 1 x n or n x 1 The matrix of , Can matrix multiplication also be understood in the way of combination ？

Have a try ：

  According to matrix multiplication, the result can be obtained

Suppose we treat each row on the left as a set of parameters （ That is to say, multiplication is xA,x On the left , Explain by line ）

So for the first line , As 1 individual And 2 individual The combination of , obtain

For the second line , As 4 individual 2-1 And 0 individual The combination of , obtain

It works ！

Conclusion ： When x No 1 x n or n x 1 Matrix time , It can be explained that the matrix contains multiple sets of parameters （ For this example 2 Group parameters , Each line in a group ）, Each set of parameters produces a result , The final target value is the combination of different parameters

---

example 4： Express the elimination process of matrix with matrix

In the first step of elimination , Let's look at the matrix A = The operation result of is set to U1 =

Hypothetical use E11 Matrix to represent the elimination operation （ The naming rule is E The subscript of is the position of the fulcrum ）, Because the current composition is based on rows , Then put the E11 This matrix needs to be on the left ,E11A = U1

E11 The first line in comes from ：1 individual A The first line in ,0 individual A The second line in ,0 individual A The third line in

E11 The second line in comes from ：-3 individual A The first line in ,1 individual A The second line in ,0 individual A The third line in

E11 The third line in comes from ：0 individual A The first line in ,0 individual A The second line in ,0 individual A The third line in

therefore E11 by

The same goes for the next step , You can get E22U1 = U2

  in general ,A After two elimination, the final U2, Expressed as E22E11A = U2

notes ： We can also put two E Merge , Put it on the right side of the equation and it turns into A = LU In the form of , Called matrix LU decompose , The details will not be expanded here

---

Add ： Matrix permutation and matrix reversible operation

Matrix arrangement （Permute）

1. Line exchange

Operate on the line , It is necessary to multiply a transformation matrix to the left of the matrix to be transformed

Form the first line on the right need 0 individual and 1 individual , Form the second line on the right need 1 individual and 0 individual , therefore E The matrix of the

2. Column exchange

Operate on Columns , It is necessary to multiply a transformation matrix to the right of the matrix to be transformed

Forming the first column on the right requires 0 individual and 1 individual , Forming the second column on the right requires 1 individual and 0 individual , therefore E The matrix of the

Invertible operation of matrix （Inverses）

The inverse operation of a matrix is the process of restoring the matrix to the identity matrix through the inverse matrix , Expressed as ：

AB = E

so to speak B yes A The inverse matrix , It can also be said that A yes B The inverse matrix （ It depends on whether you want to use rows or columns to explain , That is, which one is regarded as x）

The solution of inverse matrix can also be understood by row column combination , It is much more convenient than hard calculation

---

Gilbert Strang The teaching video of is （ Need scientific Internet ）：https://www.youtube.com/watch?v=QVKj3LADCnA&list=PL49CF3715CB9EF31D&index=2