当前位置:网站首页>CCPC 2021威海 - G. Shinyruo and KFC(组合数,小技巧)
CCPC 2021威海 - G. Shinyruo and KFC(组合数,小技巧)
2022-07-05 20:08:00 【小酒窝.】
G. Shinyruo and KFC
题意
一共有 n n n 种食物,每种食物有 a i a_i ai 个。食物个数总和不超过 1 0 5 10^5 105。
现在要把这些食物分给 k k k 个人,每个人可以拿多种事物,但每种食物最多拿 1 个。
对于 k k k 从 1 到 m m m,分别输出食物分配方案。
答案模 998244353 998244353 998244353。
1 ≤ m , n ≤ 5 ⋅ 1 0 4 1 \le m,n \le 5 \cdot 10^4 1≤m,n≤5⋅104
0 ≤ a i ≤ 1 0 5 , ∑ i = 1 n a i ≤ 1 0 5 0\le a_i\le 10^5,\ \sum_{i=1}^n a_i\le 10^5 0≤ai≤105, ∑i=1nai≤105
思路
对于一种食物共有 a i a_i ai 个,分给 k k k 个人,每人最多分一个,那么分配方案为 C ( k , a i ) C(k, ai) C(k,ai)。
那么 n 种食物,分给 k 个人总的分配方案为: ∏ i = 1 n C ( k , a i ) \prod_{i=1}^{n} C(k, a_i) ∏i=1nC(k,ai);
再遍历 m 个人,这样的话时间复杂度最低为 O(n * m),超时。
而题目中说 ai 总和不超过 1e5,那么 ai 的种类数就在 1 e 5 \sqrt {1e5} 1e5 级别,对于重复的直接用快速幂求幂次。
预处理逆元求组合数。
这样时间复杂度降为: O ( m n l o g n ) O(m \sqrt n \ logn) O(mn logn)
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define fi first
#define se second
#define endl '\n'
map<int,int> mp;
const int N = 200010, mod = 998244353;
int T, n, m;
int a[N];
struct node{
int x, cnt;
}b[N];
int fac[N], inv[N], finv[N];
int qmi(int x, int y)
{
int ans = 1;
while(y)
{
if(y & 1) ans = ans * x % mod;
x = x*x % mod;
y >>= 1;
}
return ans;
}
void init(){
fac[0]=inv[0]=inv[1]=finv[0]=finv[1]=1ll;
for(int i=1;i<N;i++)fac[i]=fac[i-1]*i%mod;
for(int i=2;i<N;i++)inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<N;i++)finv[i]=finv[i-1]*inv[i]%mod;
}
inline int C(int a,int b){
if(b>a)return 0;
else return fac[a]*finv[a-b]%mod*finv[b]%mod;
}
signed main(){
Ios;
cin >> n >> m;
for(int i=1;i<=n;i++) cin >> a[i], mp[a[i]]++;
int cnt = 0;
for(auto it : mp)
{
cnt++;
b[cnt] = {
it.first, it.second};
}
init();
for(int i=1;i<=m;i++)
{
int ans = 1;
for(int j=1;j<=cnt;j++)
{
ans = ans * qmi(C(i, b[j].x), b[j].cnt) % mod;
}
cout << ans << endl;
}
return 0;
}
经验
- 如果 n 个数的总和不超过 m,那么这些数的种类个数在 m \sqrt m m 级别。
边栏推荐
- Tasks in GStreamer
- 浅浅的谈一下ThreadLocalInsecureRandom
- Force buckle 729 My schedule I
- 【c语言】归并排序
- 图嵌入Graph embedding学习笔记
- 【数字IC验证快速入门】8、数字IC中的典型电路及其对应的Verilog描述方法
- Is the education of caiqiantang reliable and safe?
- DP: tree DP
- id选择器和类选择器的区别
- Hong Kong stocks will welcome the "best ten yuan store". Can famous creative products break through through the IPO?
猜你喜欢

Add data to excel small and medium-sized cases through poi
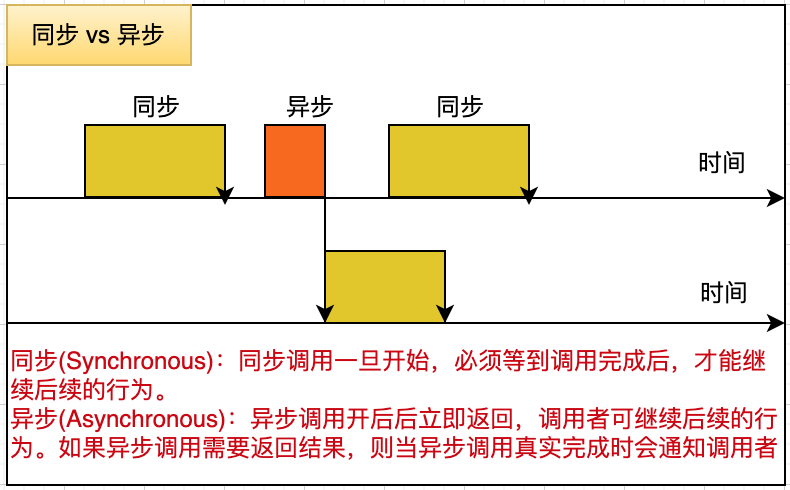
走入并行的世界
Autumn byte interviewer asked you any questions? In fact, you have stepped on thunder
Build your own website (16)
Recommended collection, my Tencent Android interview experience sharing
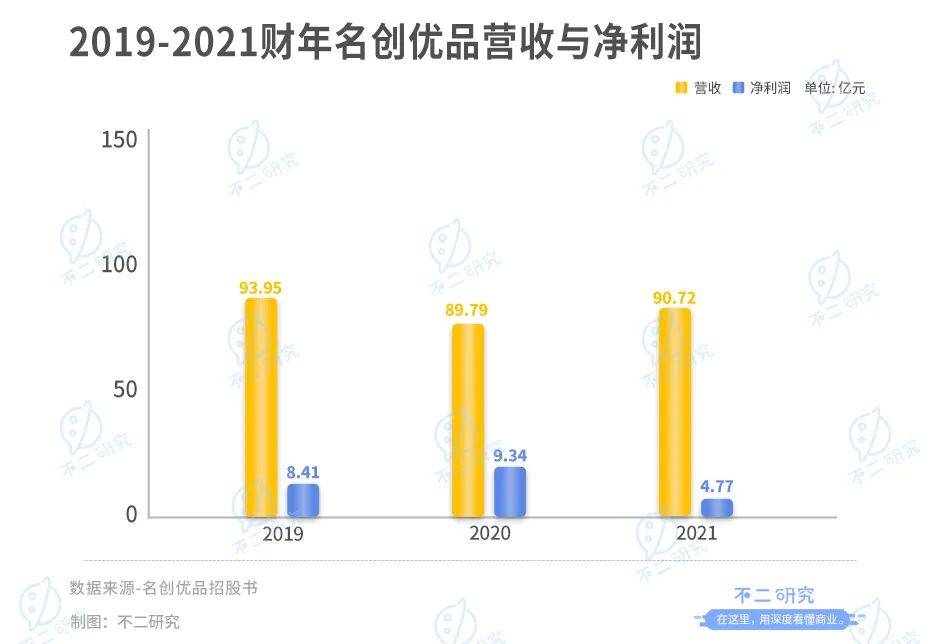
港股将迎“最牛十元店“,名创优品能借IPO突围?
零道云新UI设计中

js实现禁止网页缩放(Ctrl+鼠标、+、-缩放有效亲测)
leetcode刷题:二叉树13(相同的树)
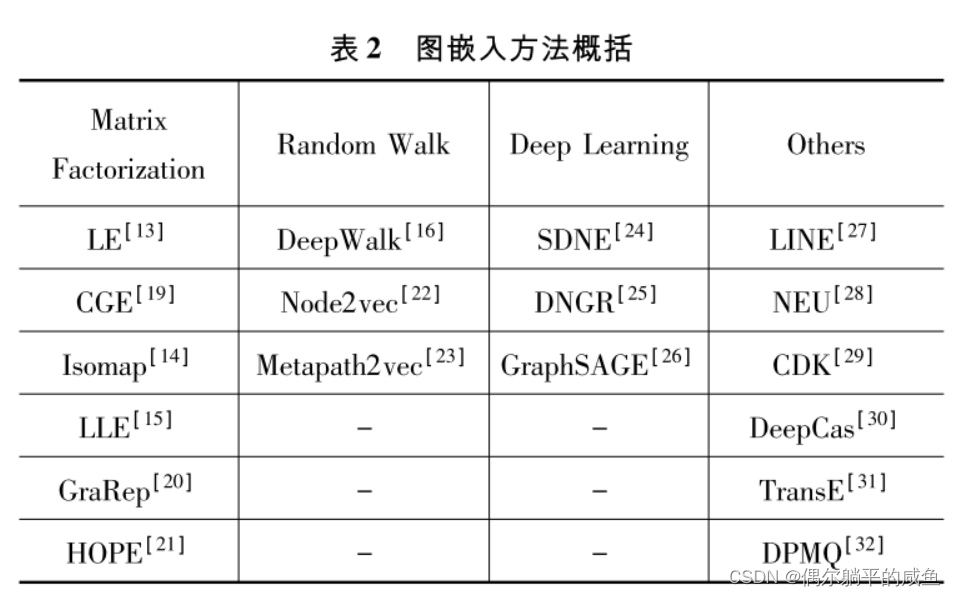
图嵌入Graph embedding学习笔记
随机推荐
使用 RepositoryProvider简化父子组件的传值
js实现禁止网页缩放(Ctrl+鼠标、+、-缩放有效亲测)
Leetcode brush question: binary tree 13 (the same tree)
2022年7月4日-2022年7月10日(ue4视频教程mysql)
1:引文;
Bitcoinwin (BCW) was invited to attend Hanoi traders fair 2022
Debezium series: record the messages parsed by debezium and the solutions after the MariaDB database deletes multiple temporary tables
leetcode刷题:二叉树10(完全二叉树的节点个数)
Where is the operation of new bonds? Is it safer and more reliable to open an account
Using repositoryprovider to simplify the value passing of parent-child components
Leetcode: binary tree 15 (find the value in the lower left corner of the tree)
Leetcode skimming: binary tree 17 (construct binary tree from middle order and post order traversal sequence)
Common operators and operator priority
多分支结构
Concept and syntax of function
再忙不能忘安全
c——顺序结构
leetcode刷题:二叉树11(平衡二叉树)
Float.floatToRawIntBits的返回值具体意思,将float转为byte数组
Parler de threadlocal insecurerandom