当前位置:网站首页>leetcode494,474
leetcode494,474
2022-07-05 00:23:00 【The left wheel of fate】
List of articles
494. Objectives and
Give you an array of integers nums And an integer target .
Add... Before each integer in the array '+' or '-' , And then concatenate all the integers , You can construct a expression :
for example ,nums = [2, 1] , Can be in 2 Before adding '+' , stay 1 Before adding '-' , And then concatenate them to get the expression "+2-1" .
Returns the 、 The result is equal to target Different expression Number of .
Example 1:
Input :nums = [1,1,1,1,1], target = 3
Output :5
explain : Altogether 5 Ways to make the ultimate goal and 3 .
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
Example 2:
Input :nums = [1], target = 1
Output :1
Tips :
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
analysis
- Change your mind , Divide into sets that only do addition and sets that do subtraction ,add and sub For the sum of each set . And that gives us
add+sub = Sum,add-sub = targetSum and target All fixed , By elimination , We can get2*add = Sum+targettherefore ,add =(Sum+target)/2, Here we need to consider whether it is possible Sum+target In the case of an odd number . If it's odd ,Sum and target It must be odd and even . - Sum If it's odd ,add and sub It must be odd and even , but add-sum It is concluded that the target Must be strange , Contradiction with odd and even .
- Sum If it's even ,add and sub It may be two odd or two even , but add-sum It is concluded that the target It must happen , Contradiction with odd and even .
- So if Sum+target For an odd number , The answer does not exist .
- Yes nums Array mapping , Make each number absolute , If the sum is less than target, It cannot exist , That is, each state with the largest number cannot add up to the largest , Then the answer does not exist . If the opposite of the sum is greater than target, It cannot exist , That is, the superposition of states with the smallest number cannot be minimized , Then the answer does not exist .
- dp open up add+1 Space ,
dp[j] Indicates that the backpack capacity is j when , The number of different expressions is dp[j] - Is still 01 knapsack , Familiar first traverse items , Then traverse the backpack in reverse , For recurrence
dp[j]+=dp[j-nums[i]], This is a recursive formula commonly used in finding combinations , Be carefuldp[0] = 1, The initial state should be set .
Code ( Dynamic programming )
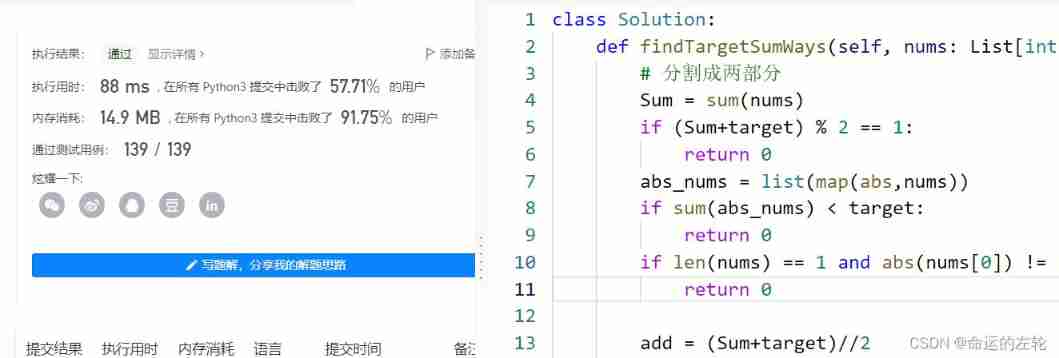
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
# Split into two parts
Sum = sum(nums)
if (Sum+target) % 2 == 1:
return 0
abs_nums = list(map(abs,nums))
if sum(abs_nums) < target or -sum(abs_nums) > target:
return 0
if len(nums) == 1 and abs(nums[0]) != abs(target):
return 0
add = (Sum+target)//2
dp = [0] * (add+1) # dp[j] The capacity is j The backpack , Yes dp[j] A way to fill
dp[0] = 1
for i in range(len(nums)): # Traverse the items
for j in range(add,nums[i]-1,-1): # Traverse the knapsack in reverse
dp[j] += dp[j - nums[i]] # fill j The method of is equal to filling j Method plus reserved space
return dp[add]
Through screenshots
474. One and zero
Here's an array of binary strings strs And two integers m and n .
Please find out and return to strs Length of the largest subset of , This subset most Yes m individual 0 and n individual 1 .
If x All of the elements of are also y The elements of , aggregate x Is a collection y Of A subset of .
Example 1:
Input :strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
Output :4
explain : At most 5 individual 0 and 3 individual 1 The largest subset of is {"10","0001","1","0"} , So the answer is 4 .
Other smaller subsets that satisfy the question include {"0001","1"} and {"10","1","0"} .{"111001"} Not satisfied with the question , Because it contains 4 individual 1 , Greater than n Value 3 .
Example 2:
Input :strs = ["10", "0", "1"], m = 1, n = 1
Output :2
explain : The largest subset is {"0", "1"} , So the answer is 2 .
Tips :
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] Only by '0' and '1' form
1 <= m, n <= 100
analysis
- two-dimensional 01 knapsack ( Think of this backpack as a flat piece of cloth )
- The two dimensions are :0 and 1 The number of
- Because it is two-dimensional 01 knapsack , We need to open up a two-dimensional array .dp[i][j] Indicates that there is a length of i, Width is j The largest subset of this cloth can have . One dimensional backpack , Generally, weight is the constraint condition or the size of number , Two dimensions have double constraints . thus , I think the three-dimensional container problem can be solved by dynamic programming , Is in a three-dimensional space , Put boxes of different sizes , How to put the highest efficiency .
- Go through the items first , Work out 0 and 1 The number of , The other two dimensions are reverse traversal , Equivalent to the capacity of the backpack .
- Because it is to find the largest subset , There must be
dp[j][z] = max(dp[j][z],dp[j-zero][z-ones]+1),+1 Is to add this traversed subset , It's very similar to when we calculate the value , discharge i The value of time isdp[i][j-1] + value[i], Empathy , Let go of j,z The number of subsets after two dimensions isdp[j-zero][z-ones]+1)
Code ( Dynamic programming )
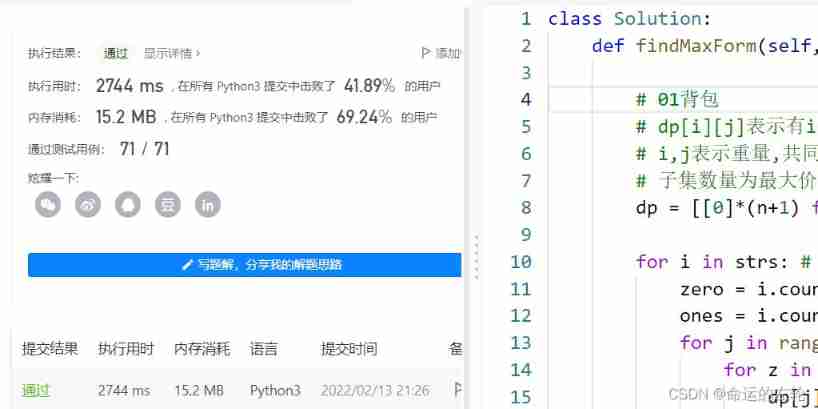
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
# 01 knapsack
# dp[i][j] Express i individual 0 Capacity and j individual 1 The largest subset of capacity backpacks can hold
# i,j It means weight , Jointly control the double boundaries
# The number of subsets is the maximum value
dp = [[0]*(n+1) for _ in range(m+1)]
for i in strs: # Traverse the items
zero = i.count('0')
ones = i.count('1')
for j in range(m,zero-1,-1):
for z in range(n,ones-1,-1):
dp[j][z] = max(dp[j][z],dp[j-zero][z-ones]+1)
return dp[m][n]
Through screenshots
If there is a mistake , Please correct me , Welcome to exchange , thank you *(・ω・)ノ
边栏推荐
- Actual combat simulation │ JWT login authentication
- lambda表达式
- Best practice case of enterprise digital transformation: introduction and reference of cloud based digital platform system security measures
- 2022.07.03 (LC 6108 decryption message)
- Learning of basic amplification circuit
- 分布式BASE理论
- TS快速入门-函数
- 公司要上监控,Zabbix 和 Prometheus 怎么选?这么选准没错!
- 业务场景功能的继续修改
- XML的解析
猜你喜欢

Réseau graphique: Qu'est - ce que le Protocole d'équilibrage de charge de passerelle glbp?

Application of fire fighting system based on 3D GIS platform
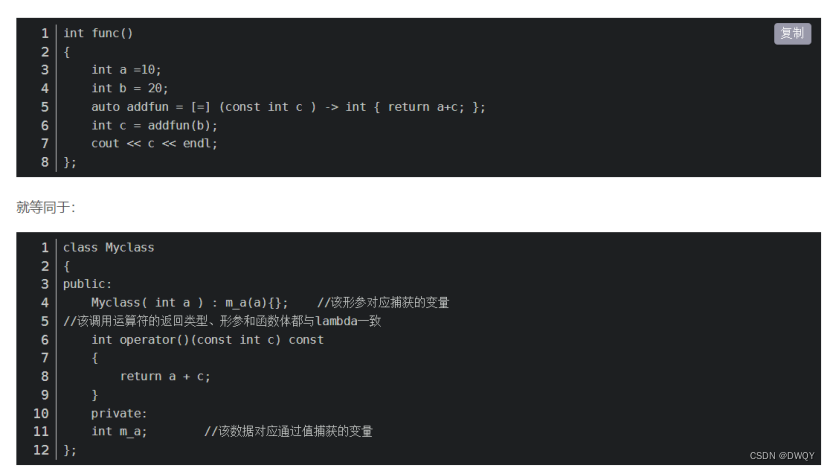
lambda表达式

Using the uniapp rich text editor
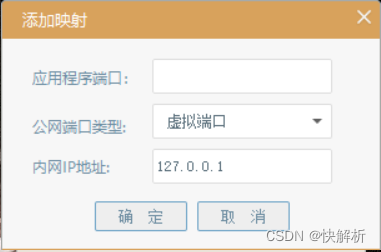
What is the difference between port mapping and port forwarding
URL和URI

Illustrated network: what is gateway load balancing protocol GLBP?
OpenHarmony资源管理详解
快解析内网穿透帮助企业快速实现协同办公

Summer challenge brings you to play harmoniyos multi terminal piano performance
随机推荐
[selenium automation] common notes
打新债开户注册安全吗?有没有风险的?靠谱吗?
【北京大学】Tensorflow2.0-1-开篇
跨域请求
uniapp微信小程序拿来即用的瀑布流布局demo2(方法二)(复制粘贴即可使用,无需做其他处理)
2022.07.03 (LC 6108 decryption message)
Specification for fs4061a boost 8.4v charging IC chip and fs4061b boost 12.6V charging IC chip datasheet
【C】(笔试题)指针与数组,指针
P4408 [NOI2003] 逃学的小孩(树的直径)
How many triangles are there in the golden K-line diagram?
How to save your code works quickly to better protect your labor achievements
lambda expressions
人生无常,大肠包小肠, 这次真的可以回家看媳妇去了。。。
Best practice case of enterprise digital transformation: introduction and reference of cloud based digital platform system security measures
Fast parsing intranet penetration helps enterprises quickly achieve collaborative office
[paper reading] cavemix: a simple data augmentation method for brain vision segmentation
图解网络:什么是网关负载均衡协议GLBP?
【报错】 “TypeError: Cannot read properties of undefined (reading ‘split‘)“
Is it safe to open and register new bonds? Is there any risk? Is it reliable?
Advanced template