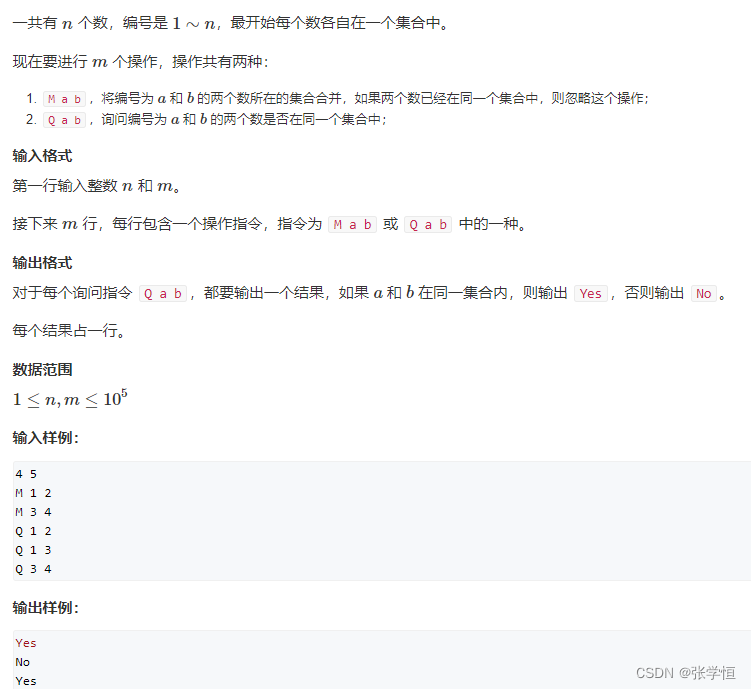
当前位置:网站首页>[combinatorics] permutation and combination (example of permutation and combination)
[combinatorics] permutation and combination (example of permutation and combination)
2022-07-03 12:06:00 【Programmer community】
List of articles
- One 、 Examples of permutations 1 ( Combine | product rule | The law of addition )
- Two 、 Examples of permutations 2
Reference blog :
- 【 Combinatorial mathematics 】 Basic counting principle ( The principle of addition | Multiplication principle )
- 【 Combinatorial mathematics 】 Examples of permutation and combination of sets ( array | Combine | Circular arrangement | binomial theorem )
- 【 Combinatorial mathematics 】 Permutation and combination ( Arrange and combine content summary | Select the question | Set arrangement | Set combination )
One 、 Examples of permutations 1 ( Combine | product rule | The law of addition )
The basic counting formula is The law of addition , product rule ;
from
1
1
1 ~
300
300
300 Take out at will
3
3
3 Number , So that the sum of these three numbers can be
3
3
3 to be divisible by , How many selection methods are there ?
Use classification ( product rule ) , Distribution ( The law of addition ) , Permutation and combination To solve the problem ;
Put the above
1
1
1 ~
300
300
300 Numbers , Divide by
3
3
3 The remainder of is divided into the following three categories :
- ① Divide
3
3
3 Remainder is
1
1
A
=
{
1
,
4
,
⋯
,
298
}
A = \{ 1, 4, \cdots , 298 \}
A={ 1,4,⋯,298}
1 :
- ② Divide
3
3
3 Remainder is
2
2
B
=
{
2
,
5
,
⋯
,
299
}
B = \{ 2, 5, \cdots , 299 \}
B={ 2,5,⋯,299}
2 :
- ③ Divide
3
3
3 Remainder is
0
0
C
=
{
3
,
6
,
⋯
,
300
}
C = \{ 3, 6, \cdots , 300\}
C={ 3,6,⋯,300}
0 :
Combination question :
stay
A
A
A Set any
3
3
3 Number , The sum of the three numbers must be
3
3
3 Multiple , Can times
3
3
3 to be divisible by ; The selection methods are
C
(
100
,
3
)
C(100, 3)
C(100,3) Kind of ;
stay
B
B
B Set any
3
3
3 Number , The sum of the three numbers must be
3
3
3 Multiple , Can times
3
3
3 to be divisible by ; The selection methods are
C
(
100
,
3
)
C(100, 3)
C(100,3) Kind of ;
stay
C
C
C Set any
3
3
3 Number , The sum of the three numbers must be
3
3
3 Multiple , Can times
3
3
3 to be divisible by ; The selection methods are
C
(
100
,
3
)
C(100, 3)
C(100,3) Kind of ;
product rule : stay
A
,
B
,
C
A,B,C
A,B,C Take a number from each set in , The sum of the three numbers is also
3
3
3 Multiple ,
- The first set takes
1
1
1 Number , Yes
100
100
100 To plant and take
- The second set takes
1
1
1 Number , Yes
100
100
100 To plant and take
- The third set takes
1
1
1 Number , Yes
100
100
100 To plant and take
All in all
10
0
3
100^3
1003 To plant and take ;
The final choice , Use the rule of addition :
3
C
(
100
,
3
)
+
10
0
3
=
1485100
3C(100, 3) + 100^3 = 1485100
3C(100,3)+1003=1485100
Two 、 Examples of permutations 2
1000
!
1000!
1000! At the end of
0
0
0 The number of ?
This value is calculated by multiplication , A very large , Basically impossible to calculate ;
List the factors : take
1000
!
1000!
1000! regard as
1000
×
999
×
998
×
⋯
×
2
×
1
1000 \times 999 \times 998 \times \cdots \times 2 \times 1
1000×999×998×⋯×2×1
Factor ;
Principle that : Among the above factors
1000
1000
1000 A factor , Will this
1000
1000
1000 Factorization , If there is
i
i
i individual
5
5
5 ,
j
j
j individual
2
2
2, be
i
i
i and
j
j
j The smaller value in
min
{
i
,
j
}
\min\{ i,j \}
min{ i,j} Namely
0
0
0 The number of ;
Above
1
1
1 ~
1000
1000
1000 this
1000
1000
1000 It is statistically decomposed from numbers
2
2
2 and
5
5
5 The number of
Statistics
2
2
2 The number of factors : Certainly more than 500 ;
- ① yes
2
2
2 The number of multiples of is
500
500
500 individual
- ② yes
4
4
4 The number of multiples of is
250
250
2
×
2
2\times2
2×2 , One of them
2
2
2 It has been counted before , Here we add
250
250
250 individual
2
2
2 , The current is
750
750
750 individual
2
2
2 ;
250 individual , Break it down
- ③ yes
16
16
16 The number of multiples of is
62
62
2
×
2
×
2
2\times2 \times 2
2×2×2 , Two of them
2
2
2 It has been counted before , Here we add
62
62
62 individual
2
2
2 , The current is
812
812
812 individual
2
2
2 ;
62 individual , Break it down
- ④ yes
32
32
32 The number of multiples of is
31
31
2
×
2
×
2
×
2
2\times2 \times 2\times 2
2×2×2×2 , Three of them
2
2
2 It has been counted before , Here we add
31
31
31 individual
2
2
2 , The current is
833
833
833 individual
2
2
2 ;
⋮
\vdots
⋮
31 individual , Break it down
Statistics
5
5
5 The number of factors :
249
249
249 individual ;
- ① yes
5
5
5 The number of multiples of is
200
200
1
1
1 A factor
5
5
5 The situation of , There must be some factors that can be decomposed into
25
,
125
,
625
25, 125, 625
25,125,625 , etc. , Next, gradually refine and peel out the factors without statistics ;
200 individual , Statistics
- ② yes
25
25
25 The number of multiples of is
40
40
5
×
5
5\times5
5×5 , One of them
5
5
5 It has been counted before , Here we add
40
40
40 individual
5
5
5 , The current is
240
240
240 individual
5
5
5 ;
40 individual , Break it down
- ③ yes
125
125
125 The number of multiples of is
8
8
5
×
5
×
5
5\times5 \times 5
5×5×5 , Two of them
5
5
5 It has been counted before , Here we add
8
8
8 individual
5
5
5 , The current is
248
248
248 individual
5
5
5 ;
8 individual , Break it down
- ④ yes
625
625
625 The number of multiples of is
1
1
5
×
5
×
5
×
5
5\times5 \times 5 \times 5
5×5×5×5 , Three of them
5
5
5 It has been counted before , Here we add
1
1
1 individual
5
5
5 , The current is
249
249
249 individual
5
5
5 ;
1 individual , Break it down
It's broken down into
2
2
2 The number of
i
i
i It must be greater than
500
500
500 Number of numbers ;
It's broken down into
5
5
5 The number of
j
j
j The value is
249
249
249 individual ;
therefore
1000
!
1000!
1000! At the end of
0
0
0 The number of yes
249
249
249 individual ;
边栏推荐
猜你喜欢
随机推荐
vulnhub之GeminiInc
ES6新特性
DEJA_ Vu3d - 054 of cesium feature set - simulate the whole process of rocket launch
vulnhub之Ripper
MCDF实验1
PHP導出word方法(一mht)
STL Tutorial 9 deep copy and shallow copy of container elements
(构造笔记)从类、API、框架三个层面学习如何设计可复用软件实体的具体技术
Oracle advanced (I) realize DMP by expdp impdp command
Vulnhub geminiinc
OpenGL shader use
Xiaopeng P7 hit the guardrail and the airbag did not pop up. The official responded that the impact strength did not meet the ejection requirements
Why can't my MySQL container start
Vulnhub's Tomato (tomato)
php 获取文件夹下面的文件列表和文件夹列表
Visual studio 2022 downloading and configuring opencv4.5.5
CGroup introduction
OpenGL index cache object EBO and lineweight mode
Flutter: about monitoring on flutter applications
DEJA_ Vu3d - cesium feature set 053 underground mode effect