当前位置:网站首页>第三讲 Gradient Tutorial梯度下降与随机梯度下降
第三讲 Gradient Tutorial梯度下降与随机梯度下降
2022-08-05 05:13:00 【长路漫漫 大佬为伴】
Gradient Tutorial
梯度下降算法与随机梯度下降的算法最主要的区别在于:
- 梯度下降算法的损失函数为 cost函数 ,cost是计算所有训练数据的损失
- 随机梯度下降算法的损失函数是loss函数,loss是计算一个训练函数的损失
- 由于随机梯度下降不需要求和,因此可以减少损失函数和梯度更新的for循环部分
梯度下降
梯度下降损失函数公式: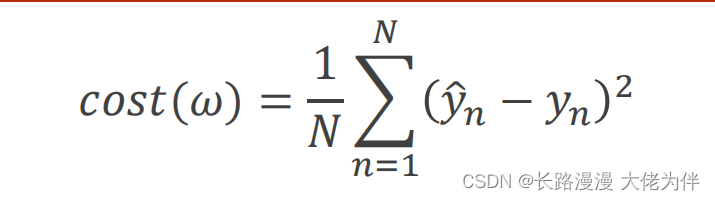
梯度公式: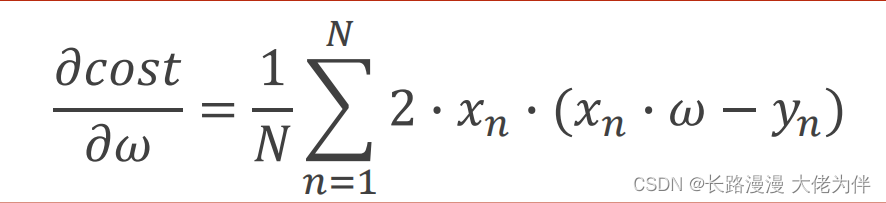
梯度下降算法(cost函数)
算法代码:
import matplotlib.pyplot as plt
# 准备x,y的数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 猜测初始权重
w = 1.0
#定义学习率,这个为超参数,需要人工定义
learning_rate=0.05
# 前馈计算
def forward(x):
return x * w
# 计算平均损失函数
# 因为需要求和,所以需要将x,y的全部数据集拿进来
def cost(xs, ys):
cost = 0
#使用zip函数分别取出x,y
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs)
# 计算梯度,同样求和并求平均值
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y)
return grad / len(xs)
epoch_list = []
cost_list = []
print('predict (before training)', 4, forward(4))
#更新梯度
for epoch in range(80):
cost_val = cost(x_data, y_data)
grad_val = gradient(x_data, y_data)
w -= learning_rate * grad_val # 0.01 learning rate
print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
#将次数与平均损失装入列表,以便于后面画图使用
epoch_list.append(epoch)
cost_list.append(cost_val)
print('predict (after training)', 4, forward(4))
#画出cost与epoch的平面图
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
结果如下:
predict (before training) 4 4.0
epoch: 0 w= 1.4666666666666668 loss= 4.666666666666667
epoch: 1 w= 1.7155555555555557 loss= 1.3274074074074067
epoch: 2 w= 1.8482962962962963 loss= 0.3775736625514398
epoch: 3 w= 1.9190913580246913 loss= 0.10739873068129853
epoch: 4 w= 1.9568487242798354 loss= 0.030548972282680543
epoch: 5 w= 1.976985986282579 loss= 0.008689485449295776
。。。。。。。。。。。。。。。。。。。
epoch: 55 w= 1.9999999999999996 loss= 3.681350891031389e-30
epoch: 56 w= 1.9999999999999998 loss= 1.3805065841367707e-30
epoch: 57 w= 2.0 loss= 3.4512664603419266e-31
epoch: 58 w= 2.0 loss= 0.0
epoch: 59 w= 2.0 loss= 0.0
。。。。。。。。。。。。。。。。。。。
epoch: 77 w= 2.0 loss= 0.0
epoch: 78 w= 2.0 loss= 0.0
epoch: 79 w= 2.0 loss= 0.0
predict (after training) 4 8.0
cost与epoch关系如图: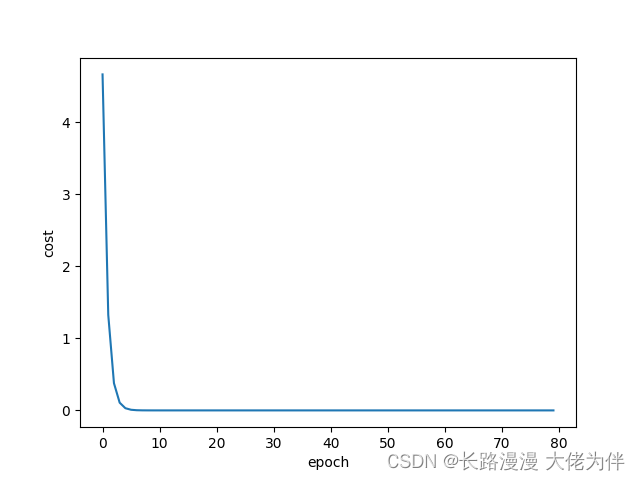
随机梯度下降
损失函数公式: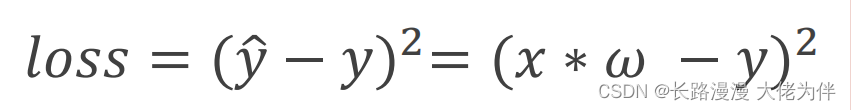
梯度公式: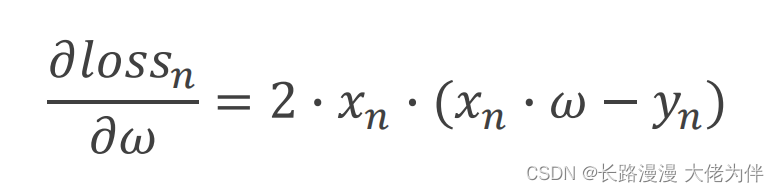
运行代码:
import matplotlib.pyplot as plt
# 准备x,y的数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 猜测初始权重
w = 1.0
#定义学习率,这个为超参数,需要人工定义
learning_rate=0.03
# 前馈计算
def forward(x):
return x * w
# 计算损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y)**2
# 计算梯度,同样求和并求平均值
def gradient(x, y):
return 2*x*(x*w - y)
epoch_list = []
loss_list = []
print('predict (before training)', 4, forward(4))
#更新梯度
for epoch in range(100):
for x,y in zip(x_data, y_data):
grad = gradient(x,y)
w = w - learning_rate*grad # update weight by every grad of sample of training set
print("\tgrad:", x, y,grad)
l = loss(x,y)
print('epoch:', epoch, 'w=', w, 'loss=', l)
#将次数与平均损失装入列表,以便于后面画图使用
epoch_list.append(epoch)
loss_list .append(l)
print('predict (after training)', 4, forward(4))
#画出cost与epoch的平面图
plt.plot(epoch_list, loss_list )
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
predict (before training) 4 4.0
grad: 1.0 2.0 -2.0
grad: 2.0 4.0 -7.52
grad: 3.0 6.0 -12.859199999999998
epoch: 0 w= 1.671376 loss= 0.9719436003840011
grad: 1.0 2.0 -0.657248
grad: 2.0 4.0 -2.4712524800000004
grad: 3.0 6.0 -4.2258417408
epoch: 1 w= 1.8920062666239998 loss= 0.10496381803637934
grad: 1.0 2.0 -0.2159874667520003
grad: 2.0 4.0 -0.8121128749875215
grad: 3.0 6.0 -1.3887130162286585
epoch: 2 w= 1.9645106673630452 loss= 0.011335434579147843
grad: 1.0 2.0 -0.0709786652739095
grad: 2.0 4.0 -0.26687978142989977
grad: 3.0 6.0 -0.4563644262451305
epoch: 3 w= 1.9883373535515134 loss= 0.0012241558996415386
grad: 1.0 2.0 -0.02332529289697316
grad: 2.0 4.0 -0.08770310129261993
grad: 3.0 6.0 -0.14997230321038302
。。。。。。。。。。。。。。。
epoch: 31 w= 1.9999999999999996 loss= 3.1554436208840472e-30
grad: 1.0 2.0 -8.881784197001252e-16
grad: 2.0 4.0 -3.552713678800501e-15
grad: 3.0 6.0 -1.0658141036401503e-14
epoch: 32 w= 1.9999999999999998 loss= 7.888609052210118e-31
grad: 1.0 2.0 -4.440892098500626e-16
grad: 2.0 4.0 -1.7763568394002505e-15
grad: 3.0 6.0 -5.329070518200751e-15
epoch: 33 w= 2.0 loss= 0.0
grad: 1.0 2.0 0.0
grad: 2.0 4.0 0.0
grad: 3.0 6.0 0.0
epoch: 34 w= 2.0 loss= 0.0
grad: 1.0 2.0 0.0
grad: 2.0 4.0 0.0
grad: 3.0 6.0 0.0
epoch: 35 w= 2.0 loss= 0.0
grad: 1.0 2.0 0.0
grad: 2.0 4.0 0.0
grad: 3.0 6.0 0.0
。。。。。。。。。。。。。。。
epoch: 97 w= 2.0 loss= 0.0
grad: 1.0 2.0 0.0
grad: 2.0 4.0 0.0
grad: 3.0 6.0 0.0
epoch: 98 w= 2.0 loss= 0.0
grad: 1.0 2.0 0.0
grad: 2.0 4.0 0.0
grad: 3.0 6.0 0.0
epoch: 99 w= 2.0 loss= 0.0
predict (after training) 4 8.0
平面图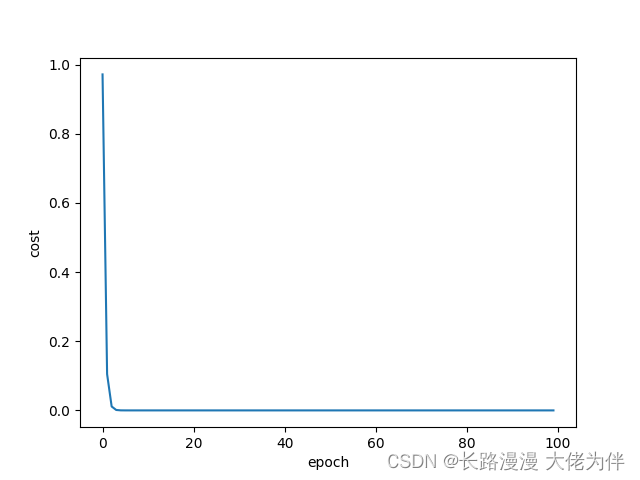
边栏推荐
- 社区分享|腾讯海外游戏基于JumpServer构建游戏安全运营能力
- Flutter learning three-Flutter basic structure and principle
- uboot enable debug printing information
- Day019 Method overriding and introduction of related classes
- server disk array
- Judgment statement _switch and case
- u-boot in u-boot, dm-pre-reloc
- 多线程查询结果,添加List集合
- Error creating bean with name ‘configDataContextRefresher‘ defined in class path resource
- 判断语句_switch与case
猜你喜欢
How can Flutter parent and child components receive click events
![[cesium] element highlighting](/img/99/504ca9802db83eb33bc6d91b34fa84.png)
[cesium] element highlighting

【过一下14】自习室的一天
Day019 Method overriding and introduction of related classes
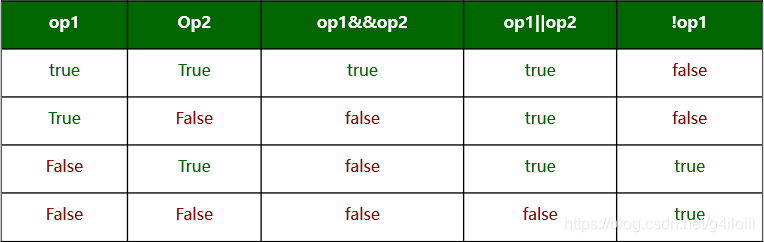
位运算符与逻辑运算符的区别
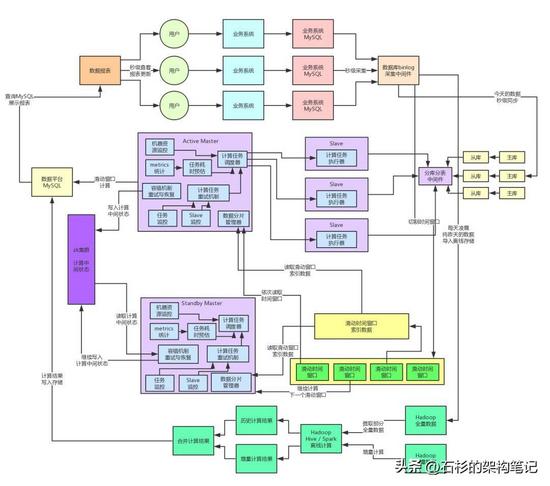
Develop a highly fault-tolerant distributed system
2022杭电多校第一场01

Basic properties of binary tree + oj problem analysis

【cesium】元素高亮显示

Difference between for..in and for..of
随机推荐
CAP+BASE
RL强化学习总结(一)
MySQL Foundation (1) - Basic Cognition and Operation
Detailed explanation of each module of ansible
【cesium】元素高亮显示
The role of DataContext in WPF
Returned object not currently part of this pool
Flutter学习三-Flutter基本结构和原理
使用二维码解决固定资产管理的难题
Requests库部署与常用函数讲解
「PHP8入门指南」PHP简明介绍
Difference between for..in and for..of
Flutter真机运行及模拟器运行
『递归』递归概念与典型实例
Requests the library deployment and common function
【技能】长期更新
[Nine Lectures on Backpacks - 01 Backpack Problems]
Flutter learning - the beginning
重新审视分布式系统:永远不会有完美的一致性方案……
Qt produces 18 frames of Cupid to express his love, is it your Cupid!!!