当前位置:网站首页>结构光三维重建(一)条纹结构光三维重建
结构光三维重建(一)条纹结构光三维重建
2022-08-05 04:57:00 【伴君】
前言
在近景三维重建领域,结构光技术可以说是应用最广泛的,尤其在工业领域。该技术目前具有高精度和无视弱纹理等优点,但复杂的室外环境还是会对该技术造成一定程度的干扰。目前用的比较多的结构光分别两大类:线结构光以及条纹结构光。接下来我先来简单介绍一下条纹结构光三维重建,事实上,条纹结构光的原理与双目立体匹配是非常相似的。
1 单目尺度不确定性
下图是一个典型的双目条纹结构光设备,由两部相机和投影仪组成,由投影仪投射结构化的光,相机捕获图像。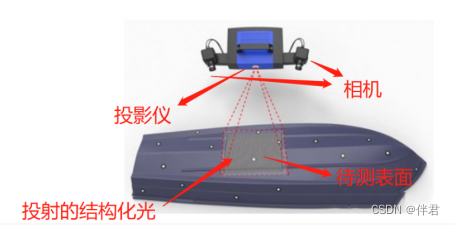
其实如果少掉投影仪,这台设备就可以看作是一个双目立体匹配相机。我们知道,双目立体匹配的工作原理在于通过左右相机拍摄到的图像视差来重建三维场景,其原理相似于人的双眼。而这其中最重要的工作,计算视差,就是要寻找左右相机图像中的同名点,效果如下所示: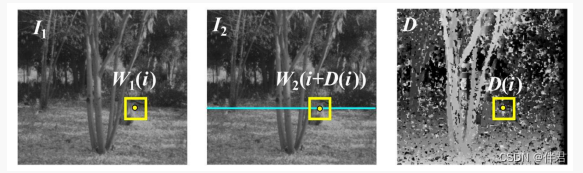
而计算机寻找同名点的方式,并不如人眼那么智能,我们通过描述子(sift,surf,orb等)找出图片中比较显著的特征点,然后对它们一一进行配对(匹配,实际上因为有极线约束的关系,这个匹配不会是n2那么复杂),最终的效果如下所示:
有了这些同名点,我们就可以依据视差计算公式(三角计算关系)来进行三维重建了。但是这个方法,存在一个致命的问题,那就是如果物体的表面没有丰富的纹理信息。这种情况,对于大部分刚加工好的工件是一个非常正常的现象,比如下图:
那如何解决呢?我们可以主动向待测量区域投射结构化的光,主动为物体表面创建“纹理”,那么问题就迎刃而解了。但事实上,这种方式依然受到物体表面材料的影响,比如说某些地方出现高反光现象等,这里先略过。
2 相移法 + 多频外差法
在结构光技术中,我们经常投影N步相移条纹来主动标记区域,投影出的条纹如下所示: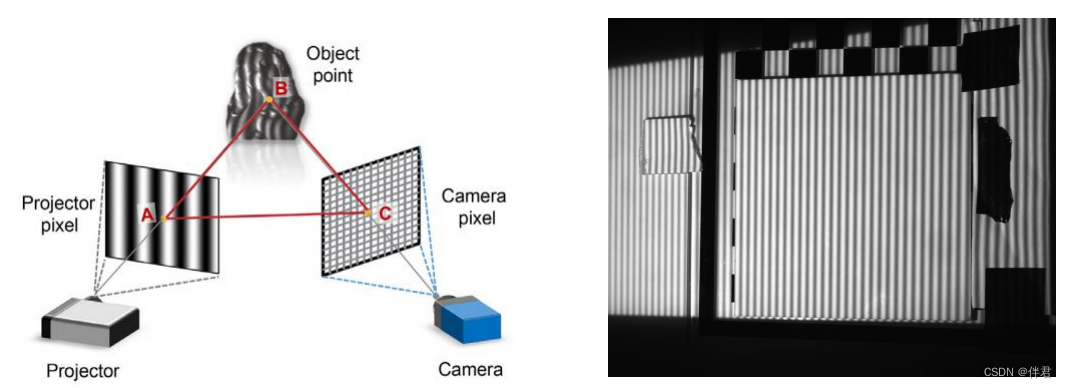
2.1 条纹生成
先来看下“计算机生成理想的,待投影仪计算投影的条纹”与”实际发生形变后,相机拍摄的条纹“的特点。特点1:单方向编码:极线约束减少搜索量;特点2:灰度反复变化:一个视场内有多个周期的条纹。
假设相移的步数为N,则生成条纹的相移公式: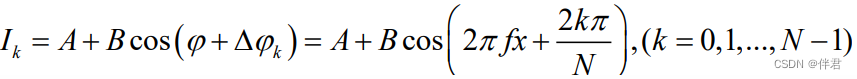
A:背景光强
B:调制强度
ϕ \phi ϕ:相位值
∇ ϕ \nabla\phi ∇ϕ:相移值
f = 1 / T :相移频率,其中T为单个周期内的像素数量,也称为条纹周期,也有的成为节距
x:编码方向上的像素坐标
(注意:通常相移法一次只能单方向编码,如果要对y方向,还需要重新生成,事实上利用极线约束,结构光算法编码单个方向就能完成重建。)
四步相移: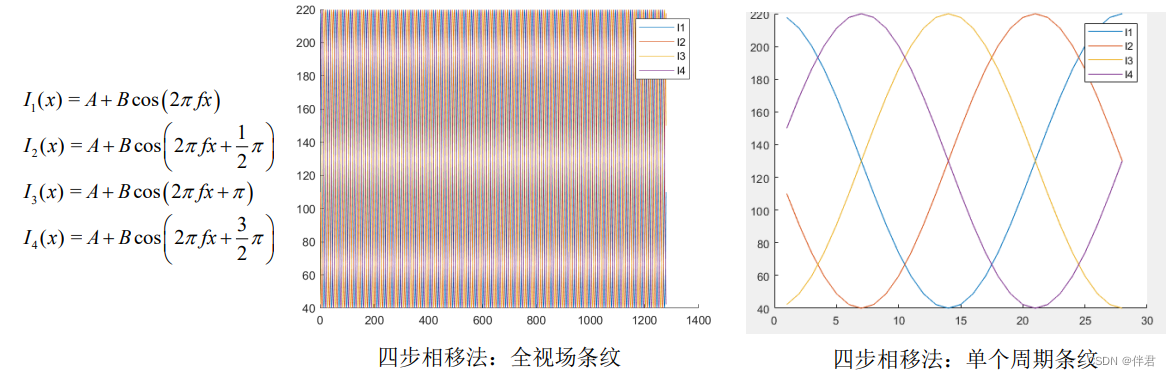
2.2 包裹相位
解相位公式(上面多个方程联立的解析解):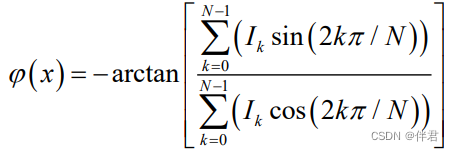
(注意:这个公式是针对单个像素成立的,因为他用的是外差的方法(类似于卫星定位,多个信号之间的差值),因而有两点:)
1.针对投影到物体后发生变形的条纹依然有效:也就是我们能够唯一标记点,在没有误差的情况下,左相机解出来的相位 ϕ \phi ϕl和右相机解出来的相位 ϕ \phi ϕr是相同的,利用双目测距模型,我们就可以计算该点的3D坐标;
2.结构光算法很容易部署在FPGA或者GPU端:达到很快的重建速度。
(注2:解出来的相位除以2Πf,就可以得到它的横坐标x,但是由于某些原因(多频外差),在计算绝对相位的时候需要进行归一化,因为我们并不会用这种方式去计算它的横坐标。)
调制度B(用于滤除噪声区域)以及误差项的计算如下: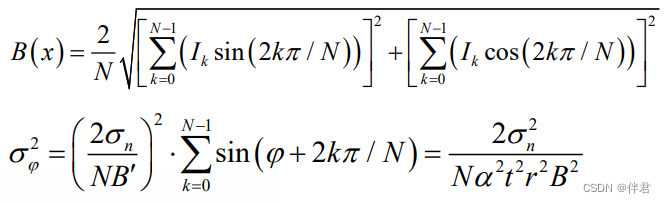
σ \sigma σn:投影亮度的标准差,是由投影仪的工艺决定的
N:相移步数;
α \alpha α:相机相应系数;
t:曝光时间;
r:物体表面发射率;
B:调制光强。
由上式可以得出两个结论:1.步长N越长,相位误差越小,事实上,增大步长N由很多好处,比如增大测量高反光的性能、降低投影仪非线性的影响,但是越长的步长意味着增大测量时间,这对某些需要动态测量的场景来说是很难接受的!2.增大调制光强,可以减小误差,但是投影仪存在非线性区域,调制度B不能无线增大。
包裹相位计算结果如下: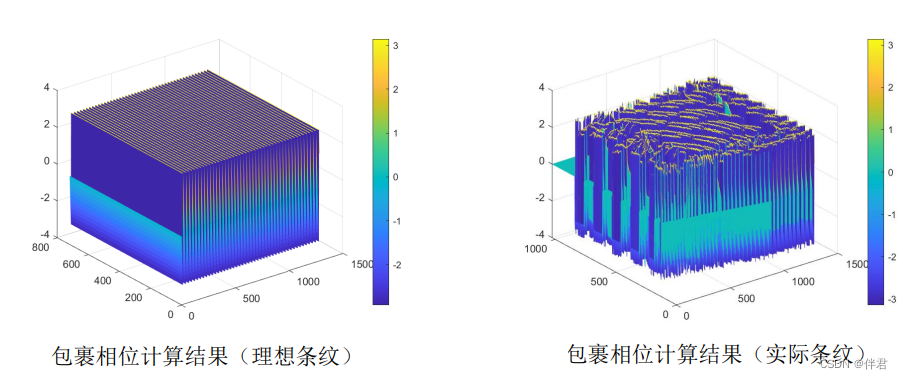
2.3 多频外差法:绝对相位
假设投影仪的分辨率为1280 x 720,编码x方向,我们即使选择最大条纹周期:T=255,即一个灰度编码一个条纹,单个周期的条纹依然不够编码全部视场范围,也就是无法消除相位歧义性: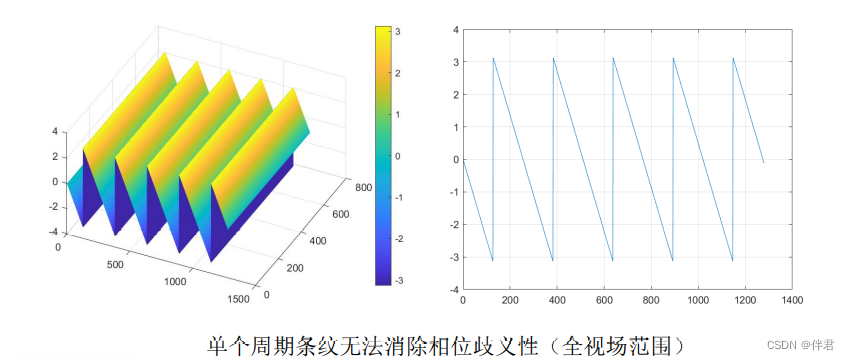
在这种情况下,假设我们知道解码出来的条纹属于第 k 个周期,也就是条纹阶数,那么它实际的相位值,也就是绝对相位即为: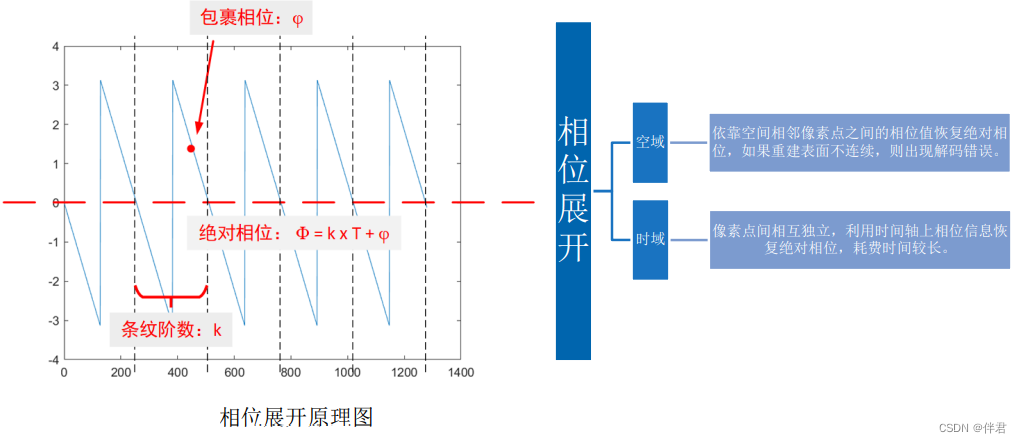
为了解算出绝对相位,在这里我们采用多频外差法,其原理是通过多个不同周期正弦光栅的相位做差,将小周期的相位主值转化为大周期的相位差,从而使得相位差信号覆盖整个视场,然后再根据相位差来得到整幅图像的绝对相位分布。
在这里以双频外差为例,原理如下图所示,其中T1、T2为条纹的周期, ϕ \phi ϕ1、 ϕ \phi ϕ2为包裹相位值,对于两者的相位差 ϕ \phi ϕ12: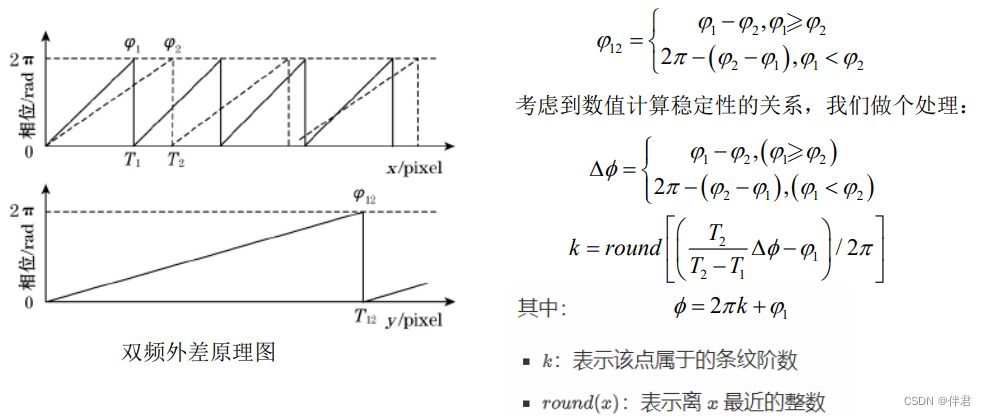
而关于周期,假设 ϕ \phi ϕ1 < ϕ \phi ϕ2,显然有: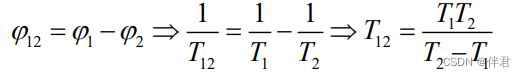
从这个周期看出:用短周期的相移条纹进行叠加,从而和获取周期更长的相移条纹,为了能够实现全场无歧义的相位展开,我们必须选择合适的T1、T2,使得T12超过整个视场,从而获得唯一相位。
(注意:双频外插还是不太够用,我们需要引入频率T3,来得到超过视场宽度的合成周期)。
3. 相移法+格雷码法
3.1 二值码与格雷码
以最简单的三位二进制码为例,亮区域:编码为1,暗区域:编码为0、假设现在我们向被测物体顺序投射三幅二进制编码图案,如下所示:(注,由于极线约束的关系,我们只需要编码一个方向,即可完成3D重建)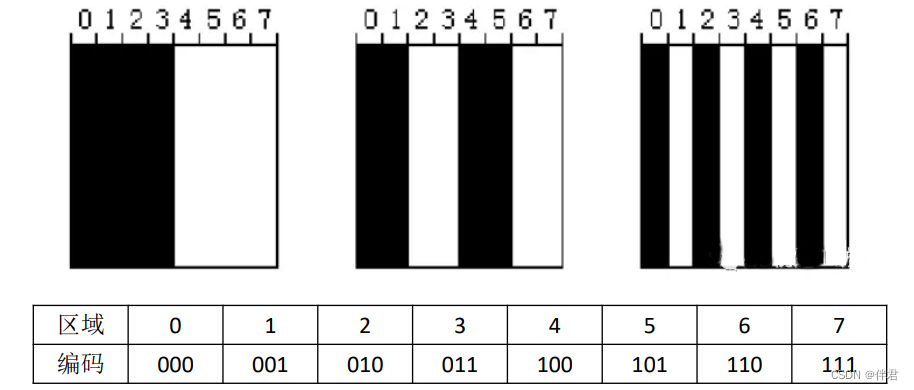
考虑单个像素点的编码在相机拍照清晰的情况下,这种编码方式当然不会出现任何问题。问题就出在:相机拍摄到的黑白相间的边界点往往是一个过渡灰度,很容易导致解码错误。在编码的最后一幅图像里,条纹都是非常细的,以上面3位编码为例,如果是
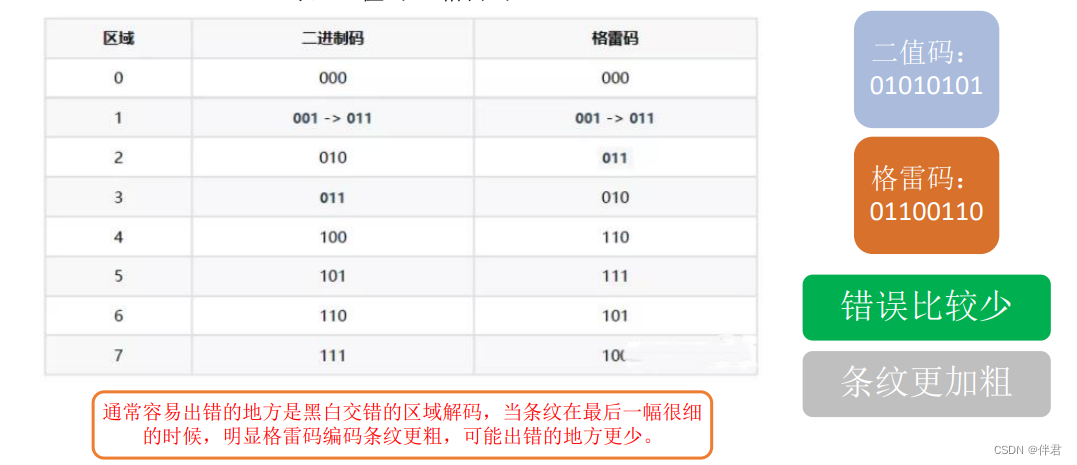
格雷码特点
3.2 格雷码+相移法所需图像的样例
算上相移条纹(N = 3), 取n = 4,另外传统相移+格雷码技术需要投影黑白两幅图像,用于二值化,生成的图像如下所示:
实际拍摄图片(N = 4):
3.3 格雷码二值化
对于格雷码解码,主要的困难在于:格雷码二值化,即如何衡量一个点是亮条纹还是暗条纹?由于环境光、以及物体表面材料原因,一副图像中像素的灰度值通常是不均匀的,但是下面这条结论是确定无疑的:二值化原则:对于同一位置,其被亮条纹照射到的亮度总是高于其被暗条纹照射的亮度!那么对于一个像素点在一张图片中的二值化,我们可以结合多幅图片来判断,具体的做法是:
但是,这类方法对于编码全为0、或者全为1的点是无效的!这个点是有的,比如说下面这幅编
码图,区域 0 全暗,区域10全亮:
因为这些点不会经历明暗变化,所以不好判断是亮条纹还是暗条纹。我们有很多办法去避免这个现象,比如说:避开这个编码;跟其他像素点亮度做比较。其中,有一种鲁棒性比较好的解决办法是,额外让所有编码编码位置都能经历全0或者全1的过程,这也是传统格雷码结合相移技术需要额外投影两幅全黑和全白图案的原因。
3.4 格雷码解码
一旦确定了二值化策略,我们就可以对每个像素求解其格雷码值,并将其映射到自然序列,据下面的公式:
解码代码如下:
3.4 相移法+格雷码具体原理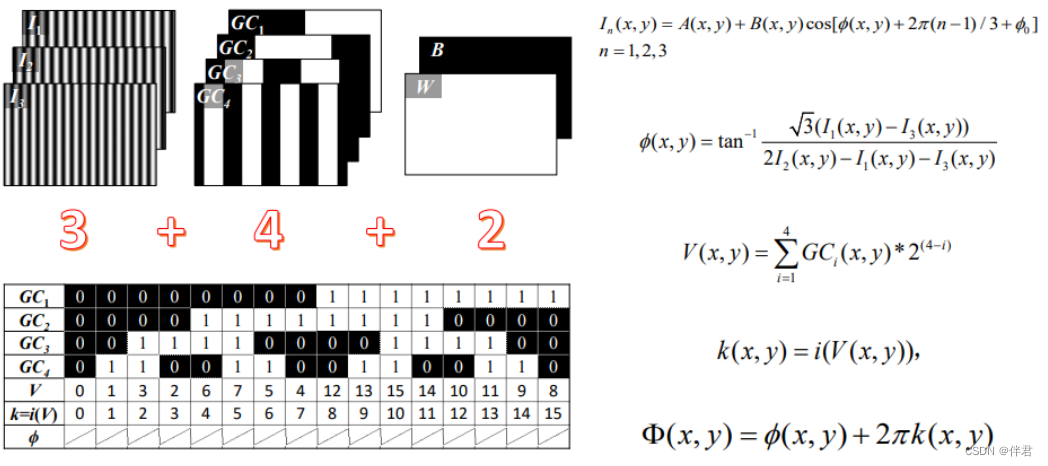
问题: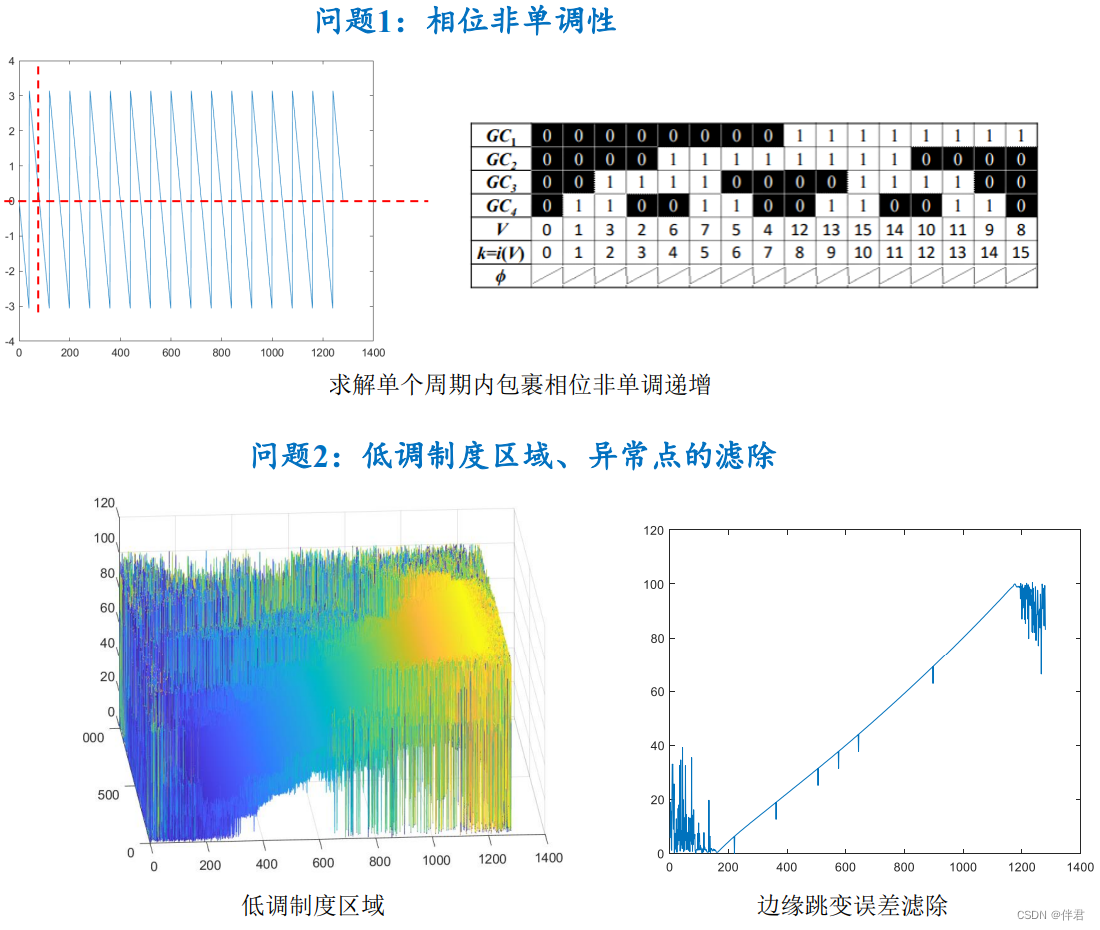
最终结果: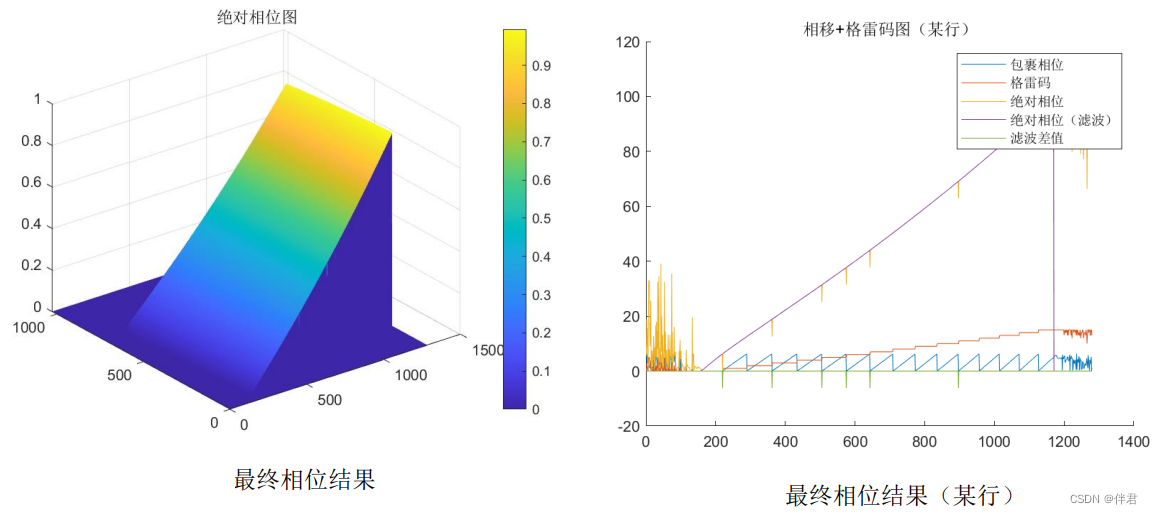
总结
最后值得一提的是有很多改进算法从效率上、精度上高于上述的算法,但是需要大家去阅读最新的论文,这里只是对结构光进行一个简单的介绍,理论比较简单,这里就不放源码了。
边栏推荐
- A 35-year-old software testing engineer with a monthly salary of less than 2W, resigns and is afraid of not finding a job, what should he do?
- The role of DataContext in WPF
- Application status of digital twin technology in power system
- 浅析主流跨端技术方案
- 作业8.4 进程间的通信 管道与信号
- Redis哨兵模式配置文件详解
- Shell(4) Conditional Control Statement
- Flutter learning 5-integration-packaging-publish
- Cron(Crontab)--use/tutorial/example
- 【cesium】加载并定位 3D Tileset
猜你喜欢
作业8.4 进程间的通信 管道与信号
The solution to the failure to read channel information when dedecms generates a message in the background

In the WebView page of the UI automation test App, the processing method when the search bar has no search button
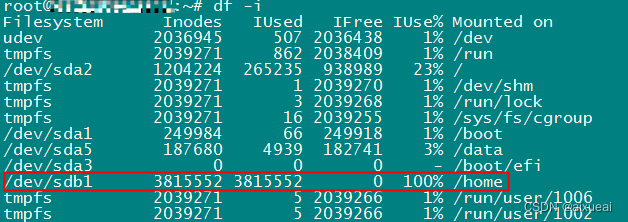
4T硬盘剩余很多提示“No space left on device“磁盘空间不足
Dephi reverse tool Dede exports function name MAP and imports it into IDA

数字孪生技术在电力系统中的应用现状

flink reads mongodb data source

什么是ASEMI光伏二极管,光伏二极管的作用

C+ +核心编程
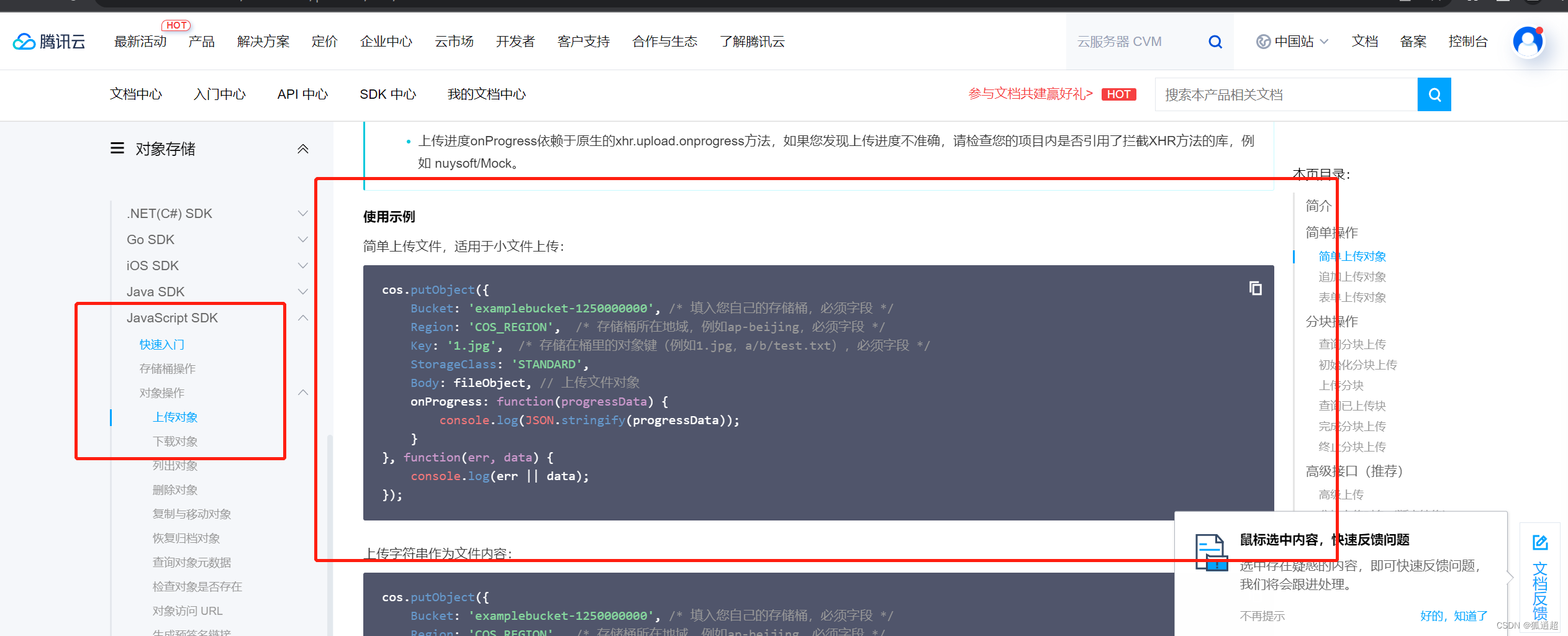
upload上传图片到腾讯云,如何上传图片
随机推荐
Shell(4)条件控制语句
In the WebView page of the UI automation test App, the processing method when the search bar has no search button
Redis哨兵模式配置文件详解
软件管理rpm
[8.1] Code Source - [The Second Largest Number Sum] [Stone Game III] [Balanced Binary Tree]
Visibility of multi-column attribute column elements: display, visibility, opacity, vertical alignment: vertical-align, z-index The larger it is, the more it will be displayed on the upper layer
服务器磁盘阵列
什么是ASEMI光伏二极管,光伏二极管的作用
Detailed explanation of Mysql's undo log
[CISCN2019 South China Division]Web11
Mysql的redo log详解
开发属于自己的node包
LeetCode:1403. 非递增顺序的最小子序列【贪心】
Dephi逆向工具Dede导出函数名MAP导入到IDA中
MySQL Foundation (1) - Basic Cognition and Operation
C语言-大白话理解原码,反码和补码
Qixi Festival earn badges
Flutter学习5-集成-打包-发布
使用IDEA连接TDengine服务器
How to solve complex distribution and ledger problems?