当前位置:网站首页>AcWing 341. Optimal trade solution (shortest path, DP)
AcWing 341. Optimal trade solution (shortest path, DP)
2022-07-02 19:43:00 【Mr. Qiao Da】
AcWing 341. The best trade
Their thinking : The first dp Aspects , take n A point is regarded as n The dividing point of two states ,dp[k] Said to k It's the dividing point , stay k Bought before , stay k Sell later ,n There will be repetition in each state , But there must be nothing missing ( Satisfy dp The condition of finding the best value ). How to ask after n A state of dp Value becomes the key , Because a graph may have rings , So you can't use state transfer directly dp, Still use spfa Find the shortest path , But the weight is transferred from edge to point , But the truth is the same . Find two shortest paths , One is to be able to reach x The lowest buying price of points , Traversal by ht The beginning adjacency table record is evaluated by the positive side , The other is seeking to reach x The maximum selling price of points , Traversal by hs The recorded inverse adjacency table is obtained , Calculate the two values of each point and then sum them up to dp value , Finally, traverse to find the largest dp The value is the answer
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10;
int ht[N], hs[N], e[M], ne[M], w[M], idx;
int n, m;
bool st[N];
int dist[N];
int dmin[N], dmax[N];
int q[N];
void add(int h[], int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++ ;
}
void spfa(int h[], int dist[], int type){
int hh = 0, tt = 1;
if(type == 0){
memset(dist, 0x3f, sizeof dmin);
dist[1] = w[1];
q[0] = 1;
}
else{
memset(dist, -0x3f, sizeof dmax);
dist[n] = w[n];
q[0] = n;
}
while(hh != tt){
int t = q[hh ++ ];
if(hh == N) hh = 0;
st[t] = false;
for(int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if((type == 0 && dist[j] > min(dist[t], w[j])) || (type == 1 && dist[j] < max(dist[t], w[j]))){
if(type == 0) dist[j] = min(dist[t], w[j]);
else dist[j] = max(dist[t], w[j]);
if(!st[j]){
q[tt ++ ] = j;
if(tt == N) tt = 0;
st[j] = true;
}
}
}
}
}
int main()
{
cin>>n>>m;
for(int i = 1; i <= n; i ++ ){
scanf("%d", &w[i]);
}
memset(ht, -1, sizeof ht);
memset(hs, -1, sizeof hs);
while(m -- ){
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(ht, x, y);
add(hs, y, x);
if(z == 2){
add(ht, y, x);
add(hs, x, y);
}
}
spfa(ht, dmin, 0);
spfa(hs, dmax, 1);
int res = 0;
for(int i = 1; i <= n; i ++ ) res = max(res, dmax[i] - dmin[i]); // seek n A state of dp value
cout<<res<<endl;
return 0;
}
边栏推荐
- AcWing 1125. Cattle travel problem solution (shortest path, diameter)
- RPD出品:Superpower Squad 保姆级攻略
- 450 Shenxin Mianjing 1
- Kt148a voice chip instructions, hardware, protocols, common problems, and reference codes
- mysql函数
- 搭建主从模式集群redis
- Idea editor removes SQL statement background color SQL statement warning no data sources are configured to run this SQL And SQL dialect is not config
- 开始练习书法
- 《重构:改善既有代码的设计》读书笔记(下)
- AcWing 342. 道路与航线 题解 (最短路、拓扑排序)
猜你喜欢
Windows2008r2 installing php7.4.30 requires localsystem to start the application pool, otherwise 500 error fastcgi process exits unexpectedly

SQLite 3.39.0 发布,支持右外连接和全外连接

450-深信服面经1

Registration opportunity of autowiredannotationbeanpostprocessor under annotation development mode

RPD product: super power squad nanny strategy

AcWing 903. 昂贵的聘礼 题解(最短路—建图、dijkstra)

Registration opportunity of autowiredannotationbeanpostprocessor in XML development mode

Data Lake (XII): integration of spark3.1.2 and iceberg0.12.1
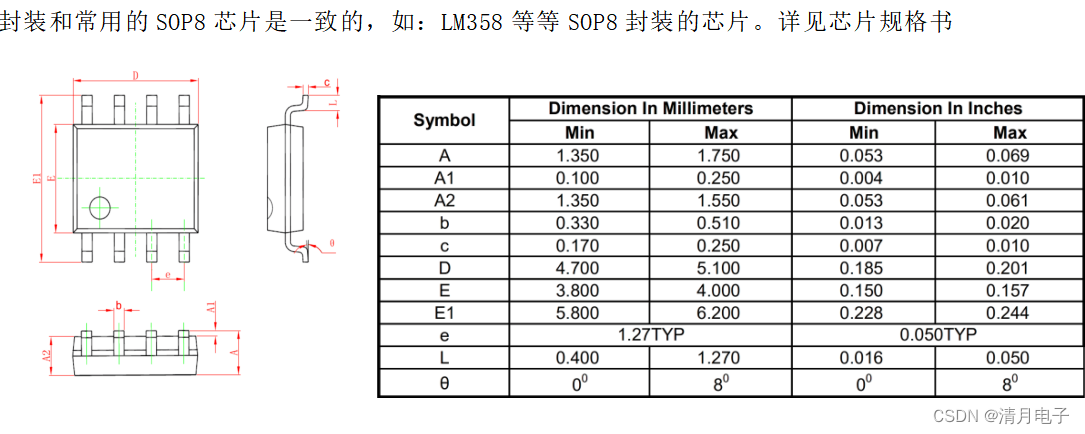
KT148A语音芯片ic的硬件设计注意事项

zabbix5客户端安装和配置
随机推荐
ShardingSphere-JDBC5.1.2版本关于SELECT LAST_INSERT_ID()本人发现还是存在路由问题
4274. 后缀表达式-二叉表达式树
高并发下如何避免产生重复数据?
A4988 drive stepper motor "recommended collection"
Yes, that's it!
IDEA编辑器去掉sql语句背景颜色SQL语句警告No data sources are configured to run this SQL...和SQL Dialect is Not Config
From 20s to 500ms, I used these three methods
函数高阶-柯里化实现
AcWing 1128. 信使 题解(最短路—Floyd)
rxjs Observable 自定义 Operator 的开发技巧
After writing 100000 lines of code, I sent a long article roast rust
自動生成VGG圖像注釋文件
职场四象限法则:时间管理四象限与职场沟通四象限「建议收藏」
Istio部署:快速上手微服务,
安装单机redis详细教程
SQLite 3.39.0 release supports right external connection and all external connection
AcWing 1127. Sweet butter solution (shortest path SPFA)
AcWing 1128. Messenger solution (shortest path Floyd)
《重构:改善既有代码的设计》读书笔记(上)
KT148A语音芯片ic的软件参考代码C语言,一线串口