[loss functions of L1, L2 and smooth L1]

---

One 、 common MSE、MAE Loss function

1.1 Mean square error 、 Loss of square

Mean square error （MSE） It is the most commonly used error in regression loss function , It is the sum of squares of the difference between the predicted value and the target value , The formula is as follows ：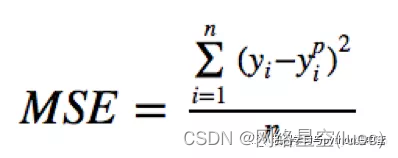

The following figure shows the curve distribution of root mean square error , The minimum value is the position where the predicted value is the target value .

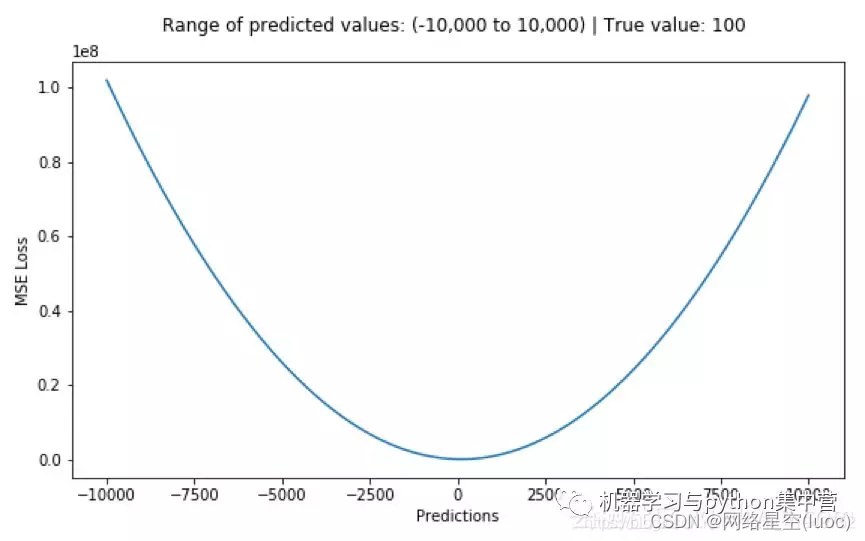
advantage ： All points are continuous and smooth , Convenient derivation , It has a more stable solution

shortcoming ： Not particularly robust , Why? ？ Because when the input value of the function is far from the central value , When using the gradient descent method, the gradient is very large , May cause gradient explosion .

What is gradient explosion ？
Error gradient is the direction and quantity of calculation in the process of neural network training , Used to update network weights with the right direction and the right amount .
In deep networks or cyclic neural networks , The error gradient can be accumulated in the update , It becomes a very large gradient , And then it leads to a big update of the network weight , And that makes the network unstable . In extreme cases , The value of the weight becomes very large , To overflow , Lead to NaN value .
Gradients between network layers （ Greater than 1.0） Exponential growth caused by repeated multiplication produces a gradient explosion .

Problems caused by gradient explosion
In deep multilayer perceptron networks , Gradient explosion can cause network instability , The best result is that you can't learn from the training data , And the worst result is something that can't be updated NaN Weight value .

1.2 Mean absolute error

Mean absolute error （MAE） Is another commonly used regression loss function , It is the sum of the absolute value of the difference between the target value and the predicted value , Represents the average error range of the predicted value , Without considering the direction of the error , The scope is 0 To ∞, The formula is as follows ：

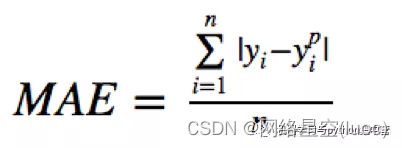
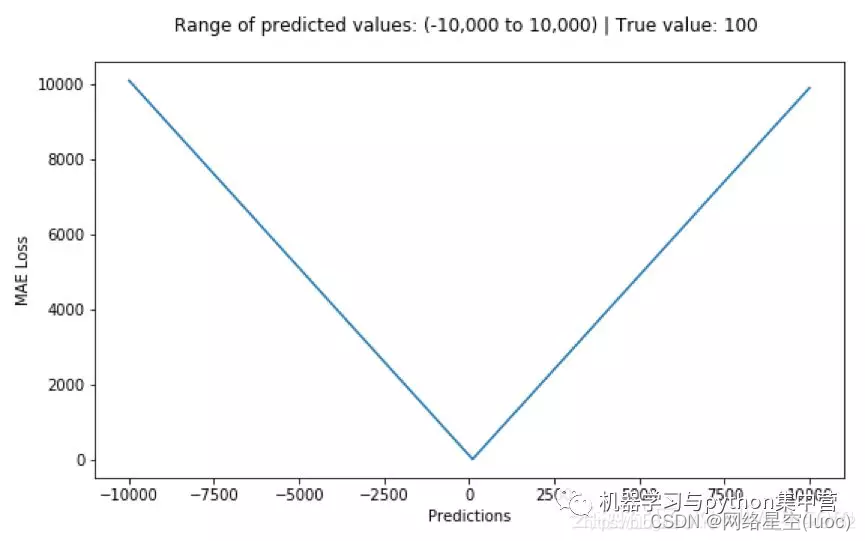
advantage ： No matter what kind of input value , All have stable gradients , It will not cause gradient explosion problems , A more robust solution .

shortcoming ： At the center point is the break point , No derivative , It's not convenient to solve .

The above two loss functions are also called L2 Loss and L1 Loss .

Two 、L1_Loss and L2_Loss

2.1 L1_Loss and L2_Loss Formula

L1 Norm loss function , Also known as the minimum absolute deviation （LAD）, Minimum absolute error （LAE）. On the whole , It is the target value （Yi) And estimates （f(xi)) The sum of the absolute differences of （S) To minimize the ：

L2 Norm loss function , Also known as least square error （LSE）. in general , It is the target value （Yi) And estimates （f(xi)) The sum of the squares of the differences （S) To minimize the ：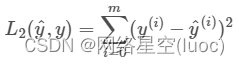

import numpy as np

def L1(yhat, y):
    loss = np.sum(np.abs(y - yhat))
    return loss

def L2(yhat, y):
    loss =np.sum(np.power((y - yhat), 2))
    return loss
# call 
yhat = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
y = np.array([1, 1, 0, 1, 1])

print("L1 = " ,(L1(yhat,y)))
print("L2 = " ,(L2(yhat,y)))

L1 Norm and L2 The difference between norm and loss function can be quickly summarized as follows ：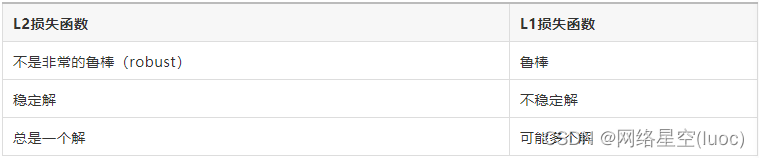

2.2 Several key concepts

（1） Robustness
The reason why the minimum absolute deviation is robust , Because it can handle outliers in data . This may be useful in studies where outliers may be safely and effectively ignored . If you need to consider any or all outliers , Then the minimum absolute deviation is the better choice .

Intuitively , because L2 Norm squares the error （ If the error is greater than 1, The error will be magnified a lot ）, The error of the model will be greater than L1 The norm is bigger , So the model will be more sensitive to this sample , This requires adjusting the model to minimize errors . If this sample is an outlier , The model needs to be adjusted to accommodate individual outliers , This will sacrifice many other normal samples , Because the error of these normal samples is smaller than that of the single outlier .

（2） stability
The instability of the minimum absolute deviation method means , For a small horizontal fluctuation of the data set , The regression line may jump a lot （ Such as , Derivation at turning point ）. On some data structures , The method has many continuous solutions ; however , A small shift in the data set , Many continuous solutions of a data structure in a certain region will be skipped . After skipping the solution in this region , The minimum absolute deviation line may have a greater inclination than the previous line .

By contraries , The solution of the least square method is stable , Because any small fluctuations in a data point , The regression line always moves only slightly ; That is to say , The regression parameter is a continuous function of the data set .

3、 ... and 、smooth L1 Loss function

As the name suggests ,smooth L1 It's after smoothing L1, As I said before L1 The disadvantage of loss is that there is a discount point , Not smooth , Leading to instability , How to make it smooth ？smooth L1 The loss function is ：

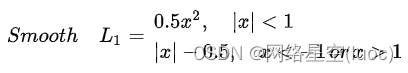
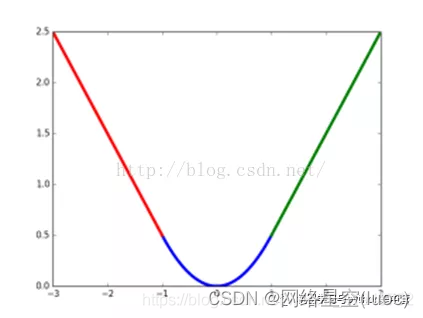
smooth L1 The loss function curve is shown in the figure below , The purpose of the author's setting is to make loss More robust to outliers , Compared with L2 Loss function , It's for outliers （ It refers to the point far from the center ）、 outliers （outlier） Insensitivity , It's not easy to control the weight of the flight .