This article has been included in Github《 Xiaobai's algorithm 》 series :https://github.com/vipstone/algorithm
This is a basic algorithm problem , The data structure involved is also what we talked about before , I'll buy a pass here first . This interview question has appeared in Amazon's interview in the past six months 28 Time , There has been a byte bounce 7 Time , The data comes from LeetCode.

Let's first look at the description of the title .
Title Description
Given an array nums And the size of the sliding window k, Please find the maximum value in all sliding windows .
Example :
Input : nums = [1,3,-1,-3,5,3,6,7], and k = 3
Output : [3,3,5,5,6,7]
Tips :
You can assume k Always effective , When the input array is not empty ,1 ≤ k ≤ Enter the size of the array .
LeetCode:https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/
title
I can't understand the above question ? No problem , Next, take a look at this picture, which can clearly describe the problem :
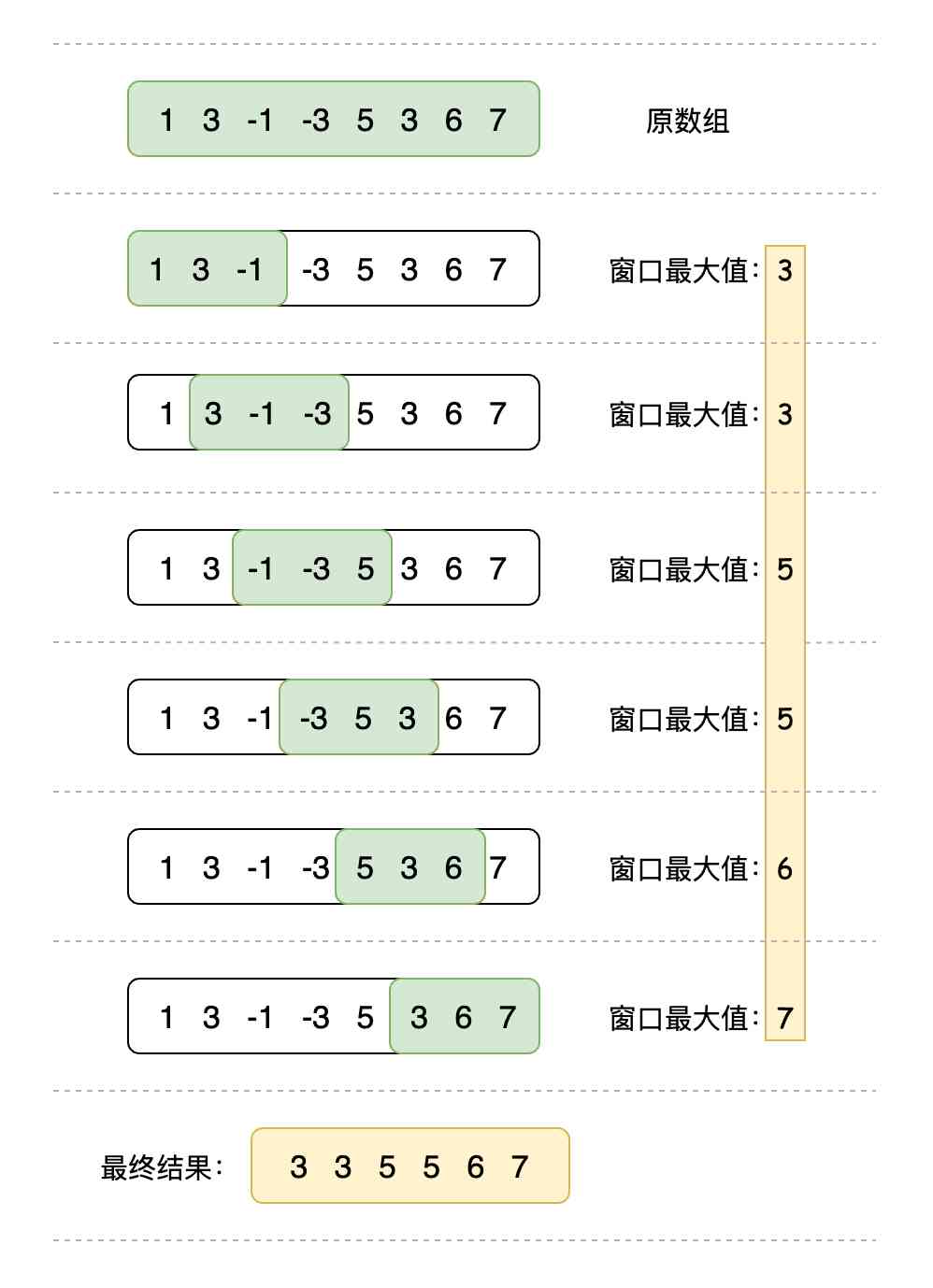
As can be seen from the above picture , The meaning of the title is : Given an array , Each query 3 The maximum of the elements , Number 3 For the size of the sliding window , Then move backward in turn to query adjacent 3 The maximum number of elements . The original array in the picture is [1,3,-1,-3,5,3,6,7], The maximum value of the final sliding window is [3,3,5,5,6,7].
After seeing this question , Our first instinct is the brute force solution , Query the maximum value of the sliding window in turn with a two-layer loop , The implementation code is as follows .
Implementation method 1: Violence solution
The implementation idea and code of brute force solution are very intuitive , As shown below :
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// Judge not empty
if (nums == null || k <= 0) return new int[0];
// The final result array
int[] res = new int[nums.length - k + 1];
for (int i = 0; i < res.length; i++) {
// Initialize maximum
int max = nums[i];
// loop k-1 Find the maximum
for (int j = i + 1; j < (i + k); j++) {
max = (nums[j] > max) ? nums[j] : max;
}
res[i] = max;
}
return res;
}
}
Submit the above code to LeetCode, The results are as follows :
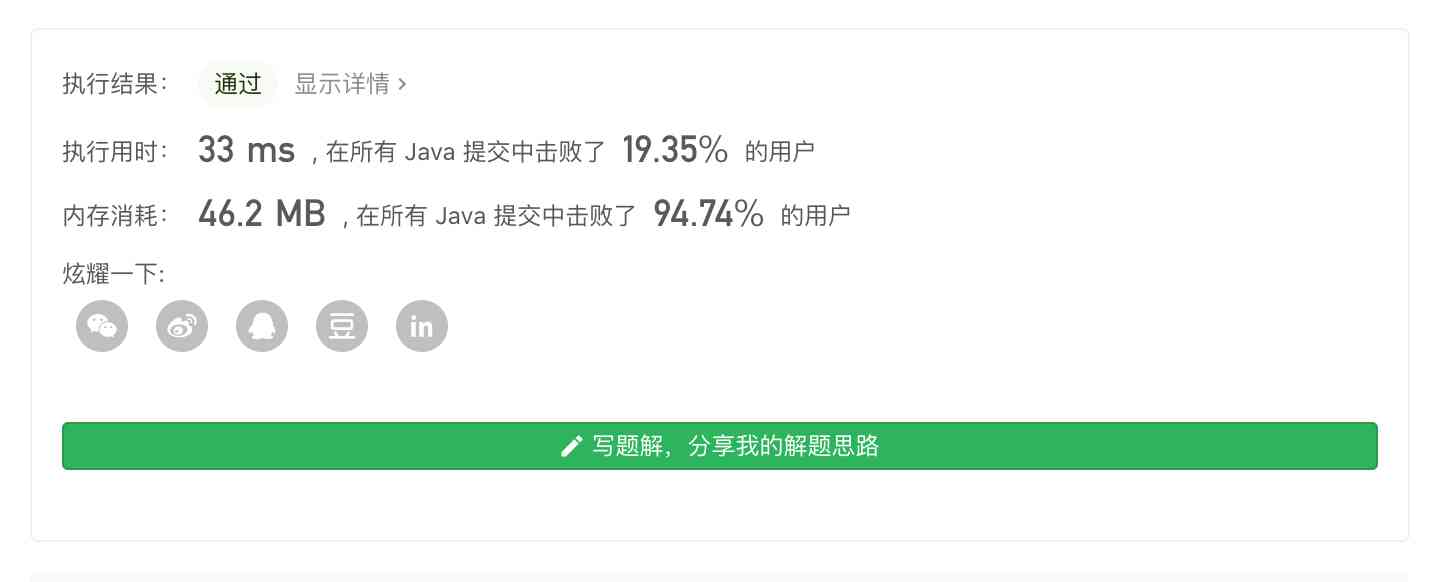
As can be seen from the above results , Although the code passed the test , But the execution efficiency is very low , This code can't be used in a production environment , So we need to keep looking for new solutions .
Implementation method 2: Improved version
Let's optimize the above method a little bit , In fact, we don't need to go through two cycles at a time , We just need a layer of loops to get the maximum value of the sliding window ( The maximum value of the previous loop element ), And then when you remove the element , Determine whether the element to be removed is the maximum value of the sliding window , If it is , The second level loop is used to find the maximum value of the new sliding window , Otherwise, just compare the maximum value with the new element , The implementation code is as follows :
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// Judge not empty
if (nums == null || k <= 0) return new int[0];
// The final result array
int[] res = new int[nums.length - k + 1];
// The value removed in the last cycle
int r = -Integer.MAX_VALUE;
// Maximum sliding window ( initialization )
int max = r;
for (int i = 0; i < res.length; i++) {
// 1. Determine the removed value , Whether it is the maximum value of the sliding window
if (r == max) {
// 2. The maximum value of the sliding window is removed , Loop to find the maximum value of the new sliding window
max = nums[i]; // Initialize maximum
// Loop to find the maximum
for (int j = i + 1; j < (i + k); j++) {
max = Math.max(max, nums[j]);
}
} else {
// 3. Just compare the maximum value of the sliding window with the new increment
max = Math.max(max, nums[i + k - 1]);
}
// The final return array record
res[i] = max;
// Record the elements to be removed in the next round
r = nums[i];
}
return res;
}
}
Submit the above code to LeetCode, The results are as follows :
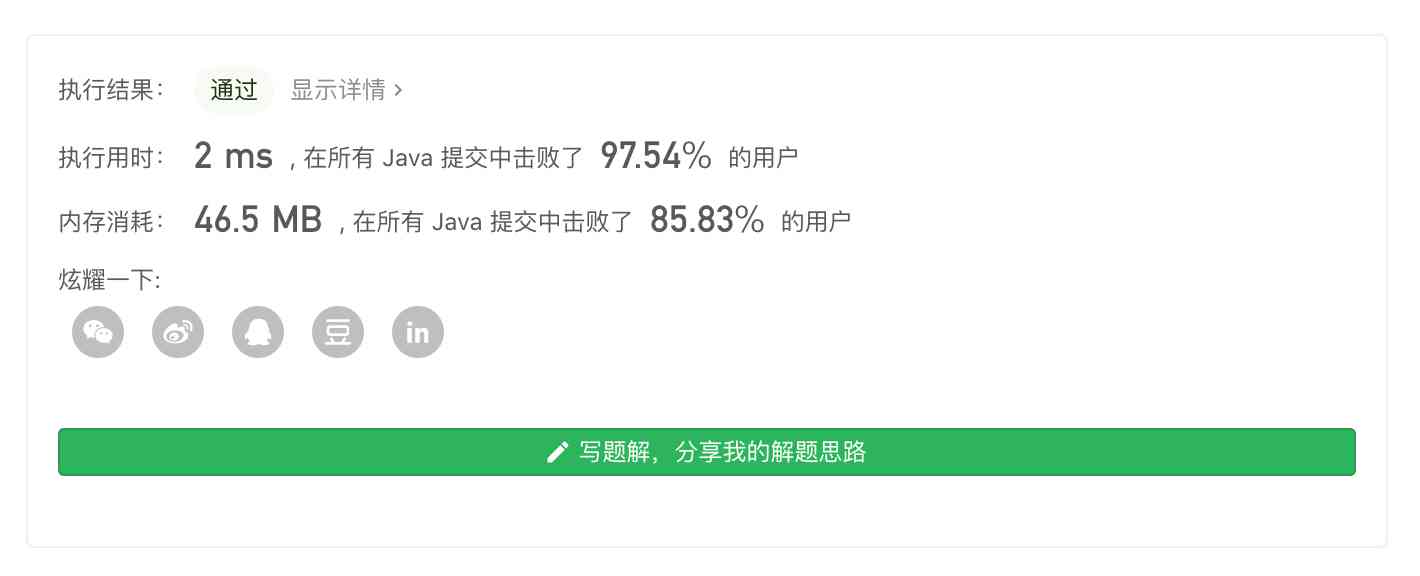
As can be seen from the above results , After the transformation, the performance has basically met my requirements , At the beginning of that article, we can also use the data structure we have learned before ? What data structure is it talking about ?
In fact, we can use 「 queue 」 To realize this topic , It's also very simple to implement , It's even more convenient than a violent solution , Now let's move on .
Implementation method 3: Priority queue
Another classic solution to this problem , Is to use the way of the largest heap to solve , The structure of the largest heap is as follows :
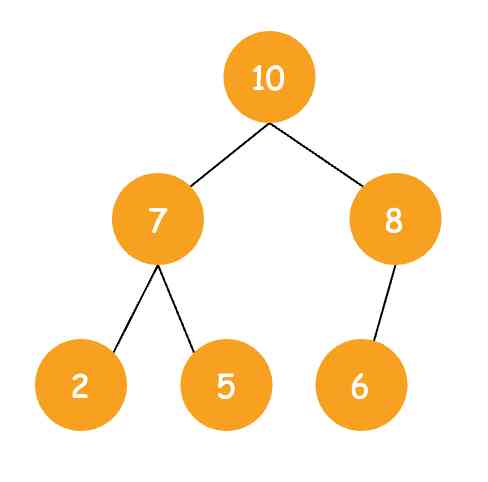
The characteristic of the largest heap is that the top of the heap is the largest element in the whole heap .
We can put the value of the sliding window into the maximum heap , This takes advantage of the characteristics of this data structure ( It will put the maximum on top of the heap ), So we can get the maximum value of the sliding window directly , The implementation code is as follows :
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// Judge not empty
if (nums == null || k <= 0) return new int[]{};
// The final result array
int[] res = new int[nums.length - k + 1];
// Priority queue
PriorityQueue<Integer> queue = new PriorityQueue(res.length, new Comparator<Integer>() {
@Override
public int compare(Integer i1, Integer i2) {
// Reverse order ( From big to small , Default is from small to large )
return i2 - i1;
}
});
// The first round of element addition
for (int i = 0; i < k; i++) {
queue.offer(nums[i]);
}
res[0] = queue.peek();
int last = nums[0]; // Elements to be removed per round
for (int i = k; i < nums.length; i++) {
// Remove elements outside the sliding window
queue.remove(last);
// Add a new element
queue.offer(nums[i]);
// Deposit the maximum value
res[i - k + 1] = queue.peek();
// Record the elements to be removed in each round ( Slide the left most element of the window )
last = nums[i - k + 1];
}
return res;
}
}
Code reading
As can be seen from the above code : The biggest pile is Java The corresponding data structure in is the priority queue PriorityQueue, But the default sorting rule of priority queue is from small to large , So we need to create a Comparator To change the sorting rules ( Sort from big to small ), Then put all the elements of the sliding window into the priority queue , So we can use it directly queue.peek() I got the maximum value of the sliding window , Then recycle to remove the edge value of the sliding window , So as to solve the problem .
Submit the above code to LeetCode, The results are as follows :
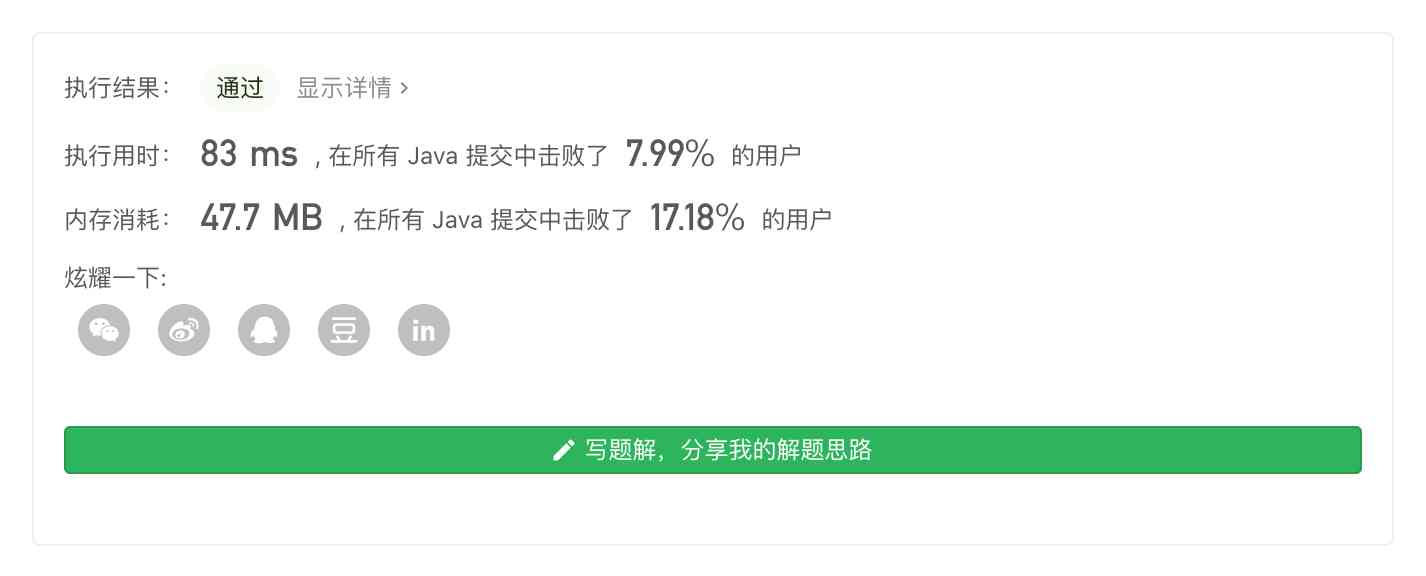
PS: From the above execution results we can see that , Using priority queues is inefficient , This is because every insert and delete requires the element order of the largest heap to be maintained again , So the efficiency of the whole execution will be very low .
Implementation method 4: deque
Besides the priority queue , We can also use the double ended queue to query the maximum value of the sliding window , Its implementation idea is very similar to that of the maximum heap , But you don't need to maintain the element position every time you add and delete , So it's going to be very efficient .
The core of the realization idea of double ended queue is to always put the maximum value of sliding window at the head of the queue ( That's the far left side of the queue ), The maximum value will be less than the maximum value on the left ( Team leader direction ) Delete all elements of . This is easy to understand , Because these relatively small values are not as large as the maximum , Before the maximum again , That is, their life cycle is shorter than the maximum , So we can delete these relatively small elements directly , As shown in the figure below :
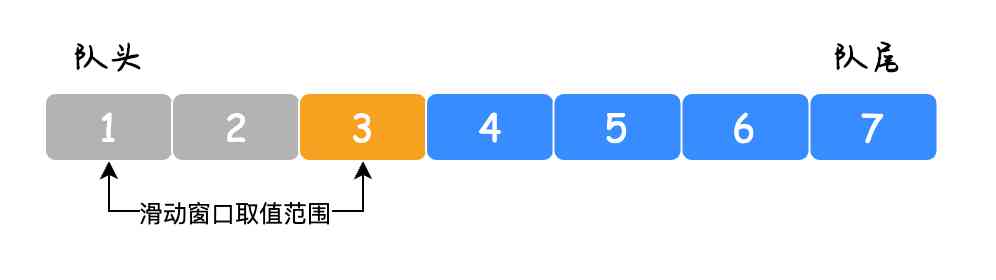
In this case , So we can put the elements 1 And elements 2 Delete .
The process of double end queue to query the maximum value of sliding window is divided into the following 4 Step :
- Remove the leftmost element that is less than the maximum value ( Make sure the maximum value of the sliding window is at the head of the team );
- Remove values from the end of the queue that are less than the current value to be added to the queue element ( Eliminate elements with small value and short life cycle );
- Add a new element to the end of the queue ;
- Add the maximum value to the array of final results .
The implementation code is as follows :
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// Judge not empty
if (nums == null || k <= 0) return new int[0];
// The final result array
int[] res = new int[nums.length - k + 1];
// The stored data is the subscript of the element
ArrayDeque<Integer> deque = new ArrayDeque();
for (int i = 0; i < nums.length; i++) {
// 1. Remove the subscript beyond the sliding window on the left
if (i >= k && (i - k) >= deque.peek()) deque.removeFirst();
// 2. Remove less than from the back nums[i] The elements of
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i])
deque.removeLast();
// 3. Subscripts join the queue
deque.offer(i);
// 4. Add the maximum value to the array
int rindex = i - k + 1;
if (rindex >= 0) {
res[rindex] = nums[deque.peek()];
}
}
return res;
}
}
Submit the above code to LeetCode, The results are as follows :
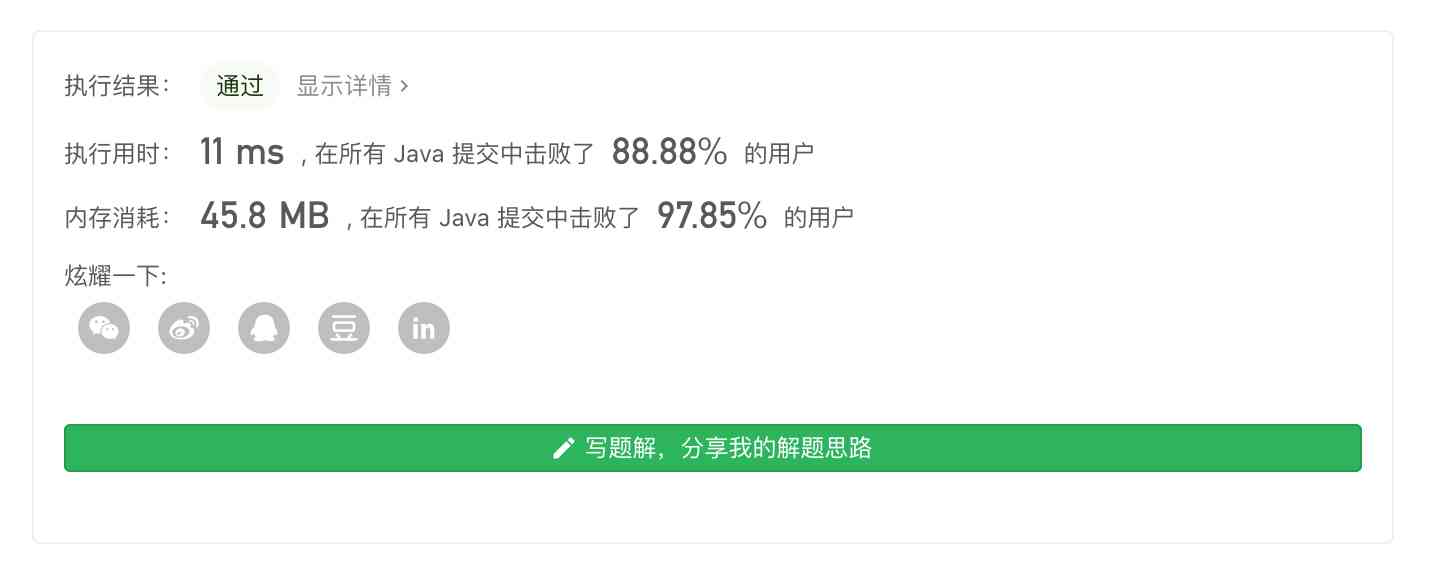
As can be seen from the above results , Compared with the priority queue, the double ended queue is , Because there is no need to recalculate and maintain the location of elements , So the execution efficiency is still very high .
summary
In this paper, we use 4 In this way, the function of finding the maximum value of sliding window is realized , The violent solution realizes this function through two layers of circulation , The code is the simplest, but the execution efficiency is not high , And through the maximum heap, that is, the priority queue to achieve ( This topic ) Although it's easier , But the implementation efficiency is not high . So we can choose to use double ended queue or improved code to achieve the maximum value of query sliding window .