当前位置:网站首页>codeforces每日5題(均1700)-第六天
codeforces每日5題(均1700)-第六天
2022-07-06 02:48:00 【湯鍵.TJ】
Pavel and barbecue
題面翻譯
【題目描述】
Pavel 在烤肉。
共有 n n n 串烤肉排成一排,各自在 n n n 個比特置中的一個。Pavel 希望每一串烤肉的每一面都能在每一個比特置上烤過一次。
Pavel 有一個全排列 p p p 和一個長為 n n n 的 0/1 序列 b b b。Pavel 每一步將比特於 i i i 的串串移到 p i p_i pi 處。同時,如果 b i = 1 b_i=1 bi=1,那麼 Pavel 將反轉這個串串。
很不幸,不是每一對 p p p 和 b b b 都滿足要求,Pavel 想知道最少修改多少個現有的 p p p 和 b b b 中的數才能滿足自己的目的。注意修改後的序列也要滿足要求。
易證這樣的 p p p 和 b b b 對於所有的 n n n 都是存在的。
【輸入格式】
第一行一個正整數 n n n,烤串的數量。
第二行 n n n 個正整數,分別錶示 p 1 , p 2 , ⋯ , p n p_1,p_2,\cdots,p_n p1,p2,⋯,pn。
第三行 n n n 個正整數,分別錶示 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn。
【輸出格式】
一行一個正整數,錶示最小的操作次數。
【數據規模與約定】
1 ≤ p i ≤ n ≤ 2 × 1 0 5 1\le p_i\le n\le 2\times 10^5 1≤pi≤n≤2×105, b i ∈ { 0 , 1 } b_i\in \{0,1\} bi∈{ 0,1}
題目描述
Pavel cooks barbecue.
There are n skewers, they lay on a brazier in a row, each on one of n positions.
Pavel wants each skewer to be cooked some time in every of n positions in two directions: in the one it was directed originally and in the reversed direction.
Pavel has a plan: a permutation p and a sequence b_{1},b_{2},…,b_{n} , consisting of zeros and ones.
Each second Pavel move skewer on position i to position p_{i} , and if b_{i} equals 1 then he reverses it.
So he hope that every skewer will visit every position in both directions.
Unfortunately, not every pair of permutation p and sequence b suits Pavel.
What is the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements?
Note that after changing the permutation should remain a permutation as well.
There is no problem for Pavel, if some skewer visits some of the placements several times before he ends to cook.
In other words, a permutation p and a sequence b suit him if there is an integer k ( k>=2n ), so that after k seconds each skewer visits each of the 2n placements.
It can be shown that some suitable pair of permutation p and sequence b exists for any n .
輸入格式
The first line contain the integer n ( 1<=n<=2·10^{5} ) — the number of skewers.
The second line contains a sequence of integers p_{1},p_{2},…,p_{n} ( 1<=p_{i}<=n ) — the permutation, according to which Pavel wants to move the skewers.
The third line contains a sequence b_{1},b_{2},…,b_{n} consisting of zeros and ones, according to which Pavel wants to reverse the skewers.
輸出格式
Print single integer — the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements.
樣例 #1
樣例輸入 #1
4
4 3 2 1
0 1 1 1
樣例輸出 #1
2
樣例 #2
樣例輸入 #2
3
2 3 1
0 0 0
樣例輸出 #2
1
提示
In the first example Pavel can change the permutation to 4,3,1,2 .
In the second example Pavel can change any element of b to 1 .
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
int n,a[N],s=0,k,ans=0;
bitset<N> sign;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&k);
s+=k;
}
for(int i=1;i<=n;i++){
if(!sign[i]){
int p=a[i];
sign[i]=1;
while(!sign[p]){
p=a[p];
}
if(p==i){
p=a[i];
while(!sign[p]){
sign[p]=1;
p=a[p];
}
}
ans++;
}
}
if(ans==1) ans=0;
if(s%2) cout<<ans<<endl;
else cout<<ans+1<<endl;
return 0;
}
Alyona and mex
題面翻譯
你有 m m m 個區間,要求構造一個長度為 n n n 的序列使得這 m m m 個區間中 mex \text{mex} mex 最小的最大( mex \text{mex} mex 定義為一個區間內沒有出現過的最小自然數)。
題目描述
Alyona’s mother wants to present an array of n non-negative integers to Alyona.
The array should be special.
Alyona is a capricious girl so after she gets the array, she inspects m of its subarrays.
Subarray is a set of some subsequent elements of the array.
The i -th subarray is described with two integers l_{i} and r_{i} , and its elements are a[l_{i}],a[l_{i}+1],…,a[r_{i}] .
Alyona is going to find mex for each of the chosen subarrays.
Among these m mexes the girl is going to find the smallest.
She wants this minimum mex to be as large as possible.
You are to find an array a of n elements so that the minimum mex among those chosen by Alyona subarrays is as large as possible.
The mex of a set S is a minimum possible non-negative integer that is not in S .
輸入格式
The first line contains two integers n and m ( 1<=n,m<=10^{5} ).
The next m lines contain information about the subarrays chosen by Alyona.
The i -th of these lines contains two integers l_{i} and r_{i} ( 1<=l_{i}<=r_{i}<=n ), that describe the subarray a[l_{i}],a[l_{i}+1],…,a[r_{i}] .
輸出格式
In the first line print single integer — the maximum possible minimum mex.
In the second line print n integers — the array a .
All the elements in a should be between 0 and 10^{9} .
It is guaranteed that there is an optimal answer in which all the elements in a are between 0 and 10^{9} .
If there are multiple solutions, print any of them.
樣例 #1
樣例輸入 #1
5 3
1 3
2 5
4 5
樣例輸出 #1
2
1 0 2 1 0
樣例 #2
樣例輸入 #2
4 2
1 4
2 4
樣例輸出 #2
3
5 2 0 1
提示
The first example: the mex of the subarray (1,3) is equal to 3 , the mex of the subarray (2,5) is equal to 3 , the mex of the subarray (4,5) is equal to 2 as well, thus the minumal mex among the subarrays chosen by Alyona is equal to 2 .
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
typedef long long ll;
int n,m,mmin=INT_MAX,l,r;
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>l>>r;
mmin=min(mmin,r-l+1);
}
cout<<mmin<<endl;
for(int i=1;i<=n;i++){
cout<<i%mmin<<" ";
}
return 0;
}
Masha and geometric depression
題面翻譯
給你一個等比數列,首項為b1,公比為q,現在Masha在黑板上從首項開始書寫這個等比數列,直到數列某項的絕對值大於l,給定m個整數,若該等比數列中的某項等同於這m個整數,則不會被寫出。
問Masha會寫出多少個數字?如果她會寫出無窮多個數字,輸出inf
注意: b1,q可能為0
題目描述
Masha really loves algebra.
On the last lesson, her strict teacher Dvastan gave she new exercise.
You are given geometric progression b defined by two integers b_{1} and q .
Remind that a geometric progression is a sequence of integers b_{1},b_{2},b_{3},… , where for each i>1 the respective term satisfies the condition b_{i}=b_{i-1}·q , where q is called the common ratio of the progression.
Progressions in Uzhlyandia are unusual: both b_{1} and q q q can equal 0 0 0 .
Also, Dvastan gave Masha m m m “bad” integers a 1 , a 2 , . . . , a m a_{1},a_{2},...,a_{m} a1,a2,...,am , and an integer l l l .
Masha writes all progression terms one by one onto the board (including repetitive) while condition |b_{i}|<=l is satisfied ( |x| means absolute value of x ).
There is an exception: if a term equals one of the “bad” integers, Masha skips it (doesn’t write onto the board) and moves forward to the next term.
But the lesson is going to end soon, so Masha has to calculate how many integers will be written on the board.
In order not to get into depression, Masha asked you for help: help her calculate how many numbers she will write, or print “inf” in case she needs to write infinitely many integers.
輸入格式
The first line of input contains four integers b_{1} , q , l , m (- 10{9}<=b_{1},q<=10{9} , 1<=l<=10^{9} , 1<=m<=10^{5} ) — the initial term and the common ratio of progression, absolute value of maximal number that can be written on the board and the number of “bad” integers, respectively.
The second line contains m distinct integers a_{1},a_{2},…,a_{m} (- 10{9}<=a_{i}<=10{9}) — numbers that will never be written on the board.
輸出格式
Print the only integer, meaning the number of progression terms that will be written on the board if it is finite, or “inf” (without quotes) otherwise.
樣例 #1
樣例輸入 #1
3 2 30 4
6 14 25 48
樣例輸出 #1
3
樣例 #2
樣例輸入 #2
123 1 2143435 4
123 11 -5453 141245
樣例輸出 #2
0
樣例 #3
樣例輸入 #3
123 1 2143435 4
54343 -13 6 124
樣例輸出 #3
inf
提示
In the first sample case, Masha will write integers 3,12,24 .
Progression term 6 will be skipped because it is a “bad” integer.
Terms bigger than 24 won’t be written because they exceed l by absolute value.
In the second case, Masha won’t write any number because all terms are equal 123 and this is a “bad” integer.
In the third case, Masha will write infinitely integers 123 .
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
typedef long long ll;
ll b1,q,l,m,k,ss=0,p=0;
set<ll> s;
int main(){
cin>>b1>>q>>l>>m;
for(int i=1;i<=m;i++){
scanf("%lld",&k);
s.insert(k);
}
ll b2=b1;
while(abs(b2)<=l){
p++;
if(s.find(b2)==s.end()){
ss++;
}
b2*=q;
if(p==1000000){
if(ss!=0&&ss!=1){
ss=-1;
}
break;
}
}
if(ss==-1) puts("inf");
else printf("%lld",ss);
return 0;
}
Minimal string
題面翻譯
給出一個字符串,按照從前到後的順序進棧,輸出字典序最小的出棧序列
題目描述
Petya recieved a gift of a string s s s with length up to 1 0 5 10^{5} 105 characters for his birthday.
He took two more empty strings t t t and u u u and decided to play a game. This game has two possible moves:
- Extract the first character of s s s and append t t t with this character.
- Extract the last character of t t t and append u u u with this character.
Petya wants to get strings s s s and t t t empty and string u u u lexicographically minimal.
You should write a program that will help Petya win the game.
輸入格式
First line contains non-empty string s s s ( 1 < = ∣ s ∣ < = 1 0 5 1<=|s|<=10^{5} 1<=∣s∣<=105 ), consisting of lowercase English letters.
輸出格式
Print resulting string u u u .
樣例 #1
樣例輸入 #1
cab
樣例輸出 #1
abc
樣例 #2
樣例輸入 #2
acdb
樣例輸出 #2
abdc
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
char b[N];
string a;
stack<char> s;
int main(){
cin>>a;
int n=a.size();
b[n-1]=a[n-1];
for(int i=n-2;i>=0;i--){
if(a[i]<b[i+1]) b[i]=a[i];
else b[i]=b[i+1];
}
for(int i=0;i<n-1;i++){
s.push(a[i]);
while(!s.empty()&&s.top()<=b[i+1]){
cout<<s.top();
s.pop();
}
}
s.push(a[n-1]);
while(!s.empty()){
cout<<s.top();
s.pop();
}
return 0;
}
Dasha and Very Difficult Problem
題面翻譯
題目大意
現有a[i],b[i]兩個數組(l<=a[i]<=b[i]<=r),我們定義p,c兩個數組,其中c[i]=b[i]-a[i],p數組是c數組的相對大小,現給你a和p數組,把任意滿足的一組b數組求出來.如果沒有滿足的,則輸出‘-1’(沒有引號).
輸入格式
第一行包含3個整數n,l,r
其中(1<=n<=10^5),(1<=l<=r<=10^9)
第二行為n個a[1],a[2],...,a[n],
第三行為n個p[1],p[2],...,p[n]
a,p的意義已在題目大意中有講述
輸出格式
一行符合條件的b數組,
若沒有符合的情况,則輸出'-1'(沒有引號)
題目描述
Dasha logged into the system and began to solve problems.
One of them is as follows:
Given two sequences a a a and b b b of length n n n each you need to write a sequence c c c of length n n n , the i i i -th element of which is calculated as follows: c i = b i − a i c_{i}=b_{i}-a_{i} ci=bi−ai .
About sequences a a a and b b b we know that their elements are in the range from l l l to r r r .
More formally, elements satisfy the following conditions: l < = a i < = r l<=a_{i}<=r l<=ai<=r and l < = b i < = r l<=b_{i}<=r l<=bi<=r .
About sequence c c c we know that all its elements are distinct.
 Dasha wrote a solution to that problem quickly, but checking her work on the standard test was not so easy.
Dasha wrote a solution to that problem quickly, but checking her work on the standard test was not so easy.
Due to an error in the test system only the sequence a a a and the compressed sequence of the sequence c c c were known from that test.
Let’s give the definition to a compressed sequence.
A compressed sequence of sequence c c c of length n n n is a sequence p p p of length n n n , so that p i p_{i} pi equals to the number of integers which are less than or equal to c i c_{i} ci in the sequence c c c .
For example, for the sequence c = [ 250 , 200 , 300 , 100 , 50 ] c=[250,200,300,100,50] c=[250,200,300,100,50] the compressed sequence will be p = [ 4 , 3 , 5 , 2 , 1 ] p=[4,3,5,2,1] p=[4,3,5,2,1] .
Pay attention that in c c c all integers are distinct.
Consequently, the compressed sequence contains all integers from 1 1 1 to n n n inclusively.
Help Dasha to find any sequence b b b for which the calculated compressed sequence of sequence c c c is correct.
輸入格式
The first line contains three integers n n n , l l l , r r r ( 1 < = n < = 1 0 5 , 1 < = l < = r < = 1 0 9 ) (1<=n<=10^{5},1<=l<=r<=10^{9}) (1<=n<=105,1<=l<=r<=109) — the length of the sequence and boundaries of the segment where the elements of sequences a a a and b b b are.
The next line contains n n n integers $a_{1},a_{2},…,a_{n} $ $ (l<=a_{i}<=r)$ — the elements of the sequence a a a .
The next line contains n n n distinct integers p 1 , p 2 , . . . , p n p_{1},p_{2},...,p_{n} p1,p2,...,pn ( 1 < = p i < = n ) (1<=p_{i}<=n) (1<=pi<=n) — the compressed sequence of the sequence c c c .
輸出格式
If there is no the suitable sequence b b b , then in the only line print “-1”.
Otherwise, in the only line print n n n integers — the elements of any suitable sequence b b b .
樣例 #1
樣例輸入 #1
5 1 5
1 1 1 1 1
3 1 5 4 2
樣例輸出 #1
3 1 5 4 2
樣例 #2
樣例輸入 #2
4 2 9
3 4 8 9
3 2 1 4
樣例輸出 #2
2 2 2 9
樣例 #3
樣例輸入 #3
6 1 5
1 1 1 1 1 1
2 3 5 4 1 6
樣例輸出 #3
-1
提示
Sequence b b b which was found in the second sample is suitable, because calculated sequence c = [ 2 − 3 , 2 − 4 , 2 − 8 , 9 − 9 ] = [ − 1 , − 2 , − 6 , 0 ] c=[2-3,2-4,2-8,9-9]=[-1,-2,-6,0] c=[2−3,2−4,2−8,9−9]=[−1,−2,−6,0](note that c i = b i − a i c_{i}=b_{i}-a_{i} ci=bi−ai ) has compressed sequence equals to p = [ 3 , 2 , 1 , 4 ] p=[3,2,1,4] p=[3,2,1,4] .
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
typedef long long ll;
ll n,l,r,a[N],p[N],b[N],mmin=INT_MAX,mmax=0;
set<ll> s;
int main(){
cin>>n>>l>>r;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&p[i]);
}
for(int i=1;i<=n;i++){
b[i]=a[i]+p[i];
mmin=min(mmin,b[i]);
mmax=max(mmax,b[i]);
}
if(mmax-mmin>r-l){
puts("-1");
}
else{
ll u=l-mmin;
for(int i=1;i<=n;i++){
printf("%lld ",b[i]+u);
}
}
return 0;
}
边栏推荐
- C语言sizeof和strlen的区别
- Pat 1046 shortest distance (20 points) simulation
- 球面透镜与柱面透镜
- [Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 19
- MySQL winter vacation self-study 2022 11 (7)
- 有没有完全自主的国产化数据库技术
- 微服务间通信
- The difference between sizeof and strlen in C language
- Follow the mouse's angle and keyboard events
- Httprunnermanager installation (III) - configuring myql Database & initialization data under Linux
猜你喜欢
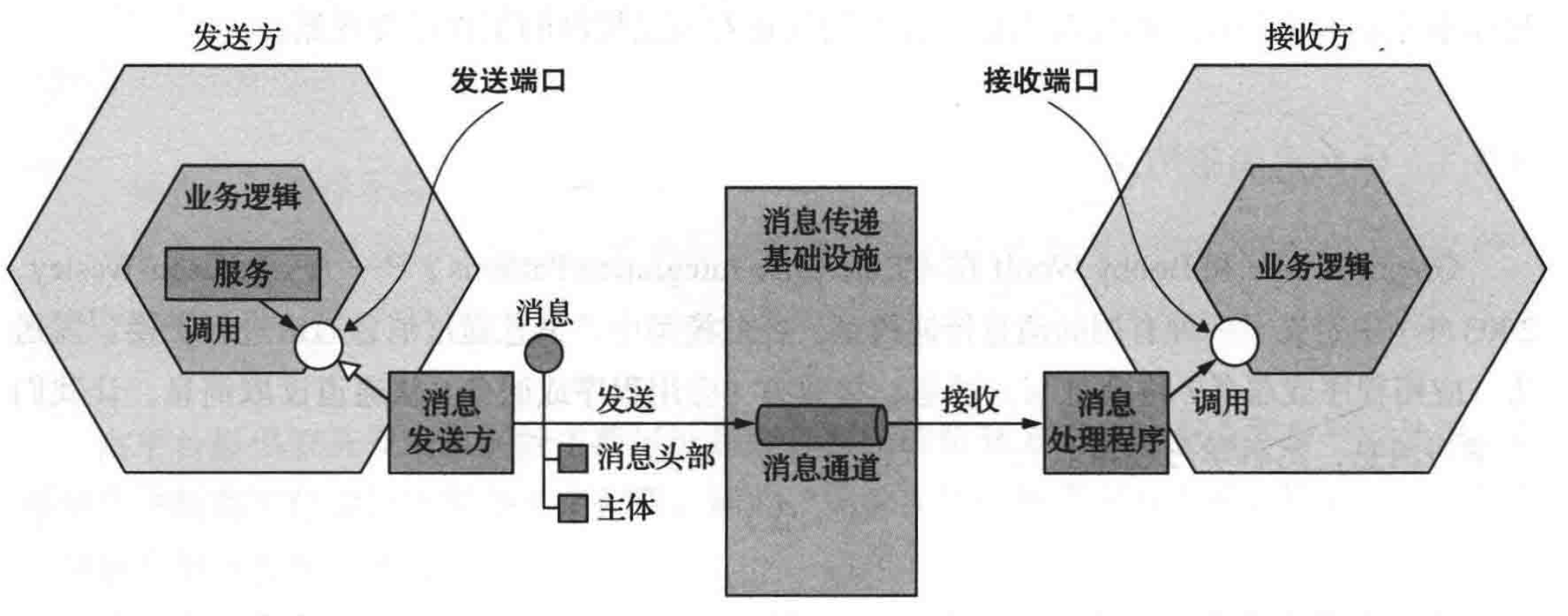
微服务间通信
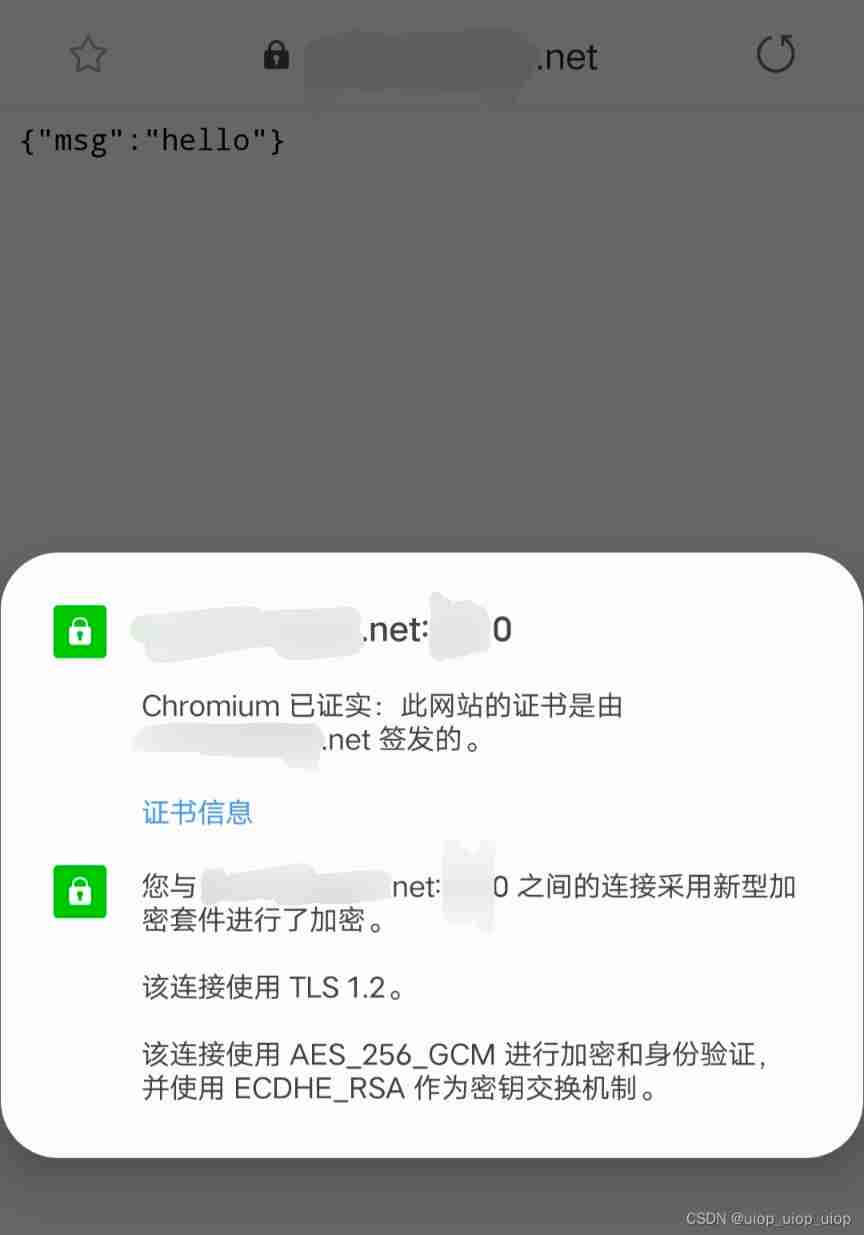
Sign SSL certificate as Ca
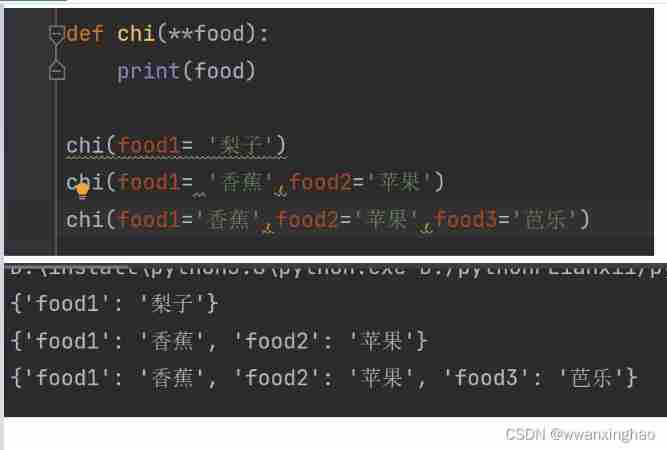
1. Dynamic parameters of function: *args, **kwargs
![[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 11](/img/6a/398d9cceecdd9d7c9c4613d8b5ca27.jpg)
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 11
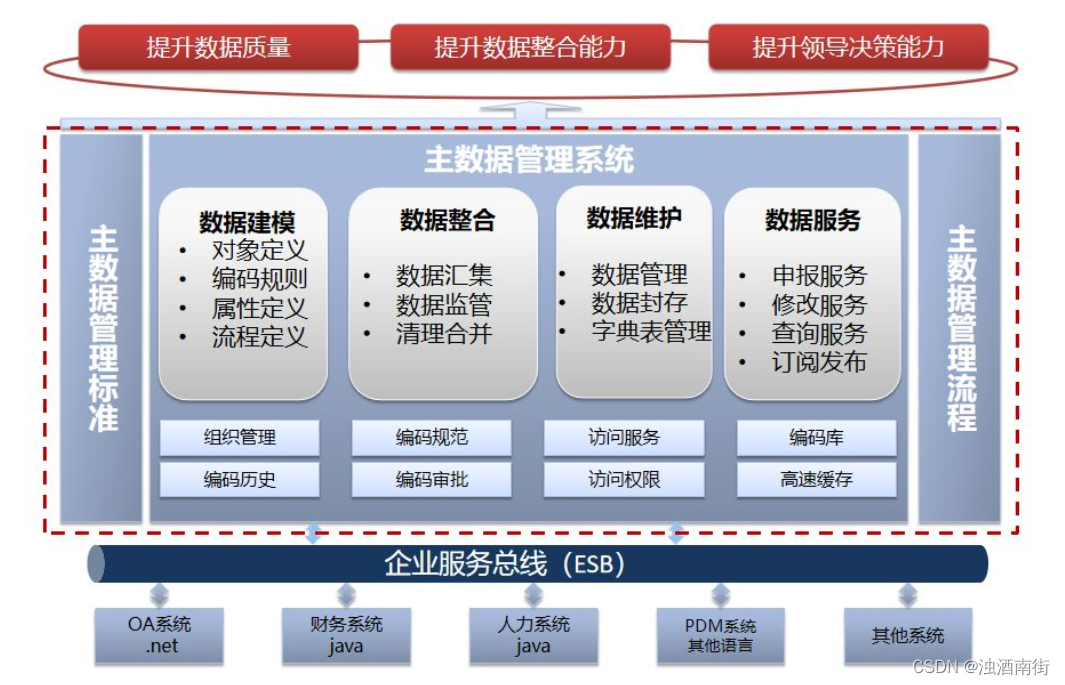
Master data management theory and Practice
![[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 18](/img/1a/94ef8be5c06c2d1c52fc8ce7f03ea7.jpg)
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 18
![[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 15](/img/72/0fe9cb032339d5f1ccf6f6c24edc57.jpg)
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 15
![[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 19](/img/7c/f728e88ca36524f92c56213370399b.jpg)
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 19
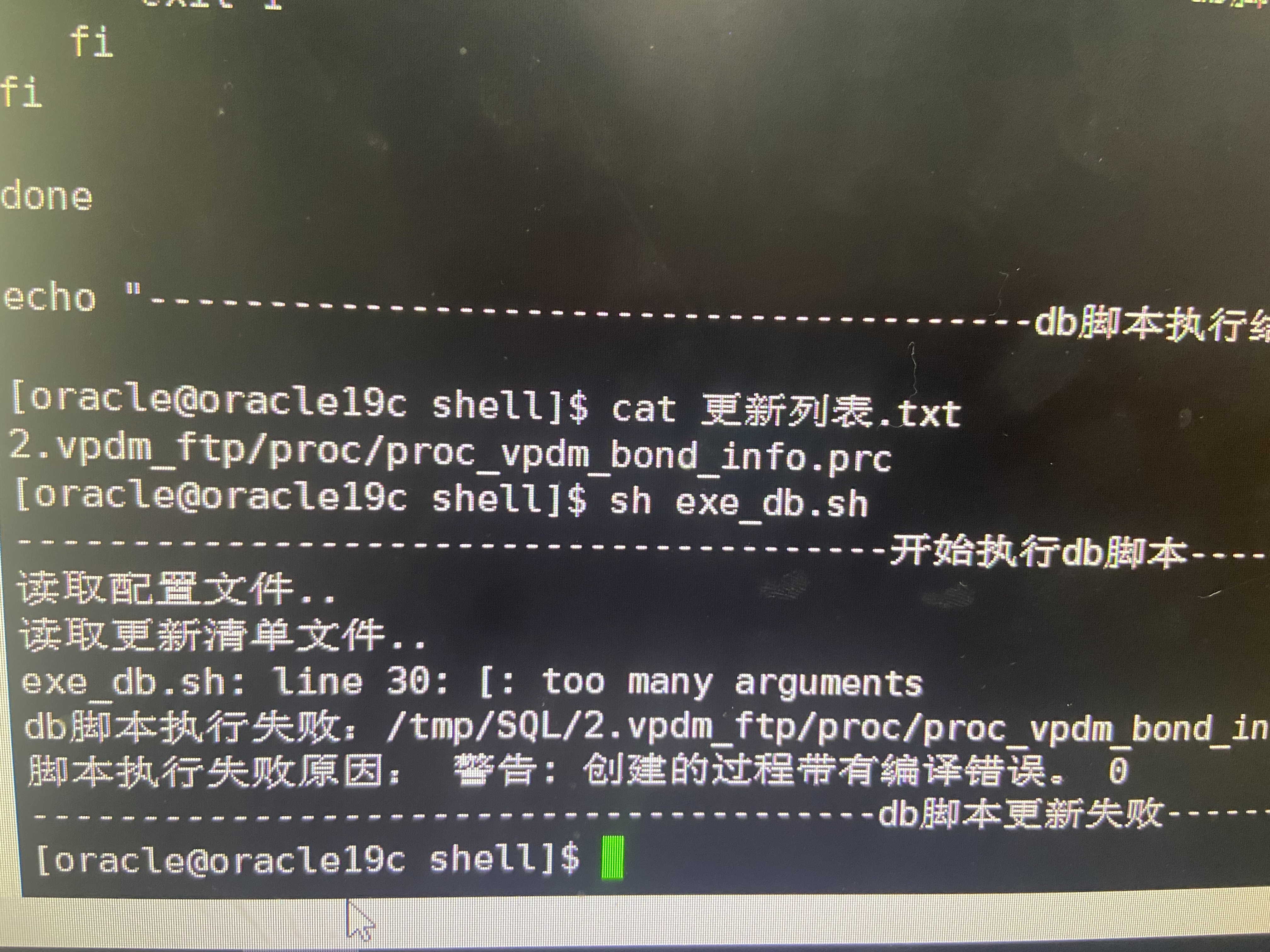
Shell script updates stored procedure to database
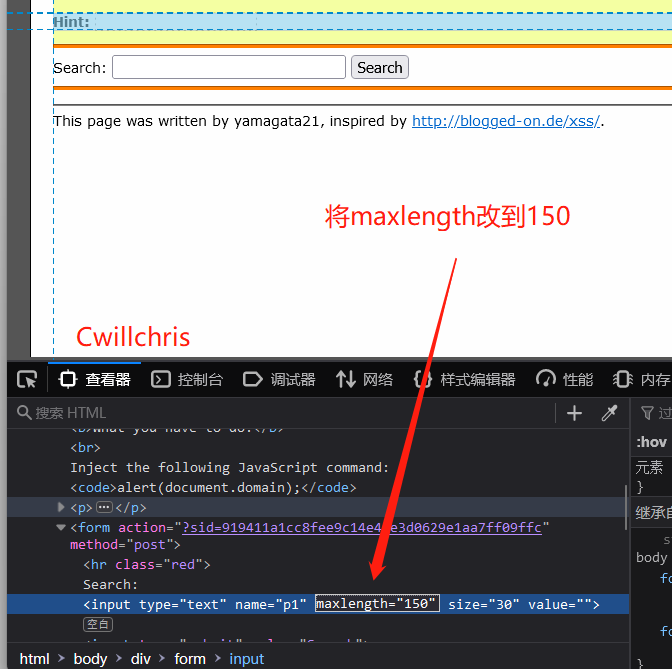
XSS challenges绕过防护策略进行 XSS 注入
随机推荐
GifCam v7.0 极简GIF动画录制工具中文单文件版
PMP每日一练 | 考试不迷路-7.5
QT release exe software and modify exe application icon
[unity3d] GUI control
How to accurately identify master data?
Maturity of master data management (MDM)
I changed the driver to 5.1.35, but it is still the same error. I can succeed even now, but I will report this every time I do an SQL operation
【若依(ruoyi)】设置主题样式
C language - Blue Bridge Cup - promised score
Referenceerror: primordials is not defined error resolution
2020.02.11
"Hands on learning in depth" Chapter 2 - preparatory knowledge_ 2.3 linear algebra_ Learning thinking and exercise answers
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 22
Solution: attributeerror: 'STR' object has no attribute 'decode‘
Blue Bridge Cup group B provincial preliminaries first question 2013 (Gauss Diary)
DDoS "fire drill" service urges companies to be prepared
The difference between sizeof and strlen in C language
Classic interview question [gem pirate]
不赚钱的科大讯飞,投资价值该怎么看?
Universal crud interface