"Hands on learning in depth" Chapter 2 - preparatory knowledge_ 2.5 automatic differentiation_ Learning thinking and exercise answers

---

2.5. Automatic differentiation

author github link ： github link

practice

1. Prove a matrix $\mathbf{A}$ The transpose of is $\mathbf{A}$, namely $({\mathbf{A}}^{\top }{)}^{\top }=\mathbf{A}$.
2. Two matrices are given $\mathbf{A}$ and $\mathbf{B}$, prove “ They are transposed and ” be equal to “ They are transposed with ”, namely ${\mathbf{A}}^{\top }+{\mathbf{B}}^{\top }=(\mathbf{A}+\mathbf{B}{)}^{\top }$.
3. Given an arbitrary square matrix $\mathbf{A}$,$\mathbf{A}+{\mathbf{A}}^{\top }$ Is it always symmetrical ? Why? ?
4. We define shapes in this section $(2,3,4)$ Tensor X.len(X) What is the output of ？
5. For tensors of arbitrary shape X,len(X) Whether it always corresponds to X The length of a particular axis ? What is this axis ?
6. function A/A.sum(axis=1), See what happens . Can you analyze the reason ？
7. Consider a with a shape $(2,3,4)$ Tensor , In the shaft 0、1、2 What shape is the summation output on ?
8. by linalg.norm Function provides 3 Tensors of one or more axes , And observe its output . For tensors of any shape, what does this function calculate ?

Practice reference answers

1. Why is it more expensive to calculate the second derivative than the first derivative ？
   Because the second derivative is based on the calculation of the first derivative , Therefore, the cost of calculating the second derivative must be greater than that of the first derivative
2. After running the back propagation function , Run it again now , See what happens .
   The complains , about Pytorch Come on , The forward process establishes a calculation diagram , Release after back propagation . Because the intermediate result of the calculation graph has been released , So the second run of back propagation will make an error . At this moment in backward Add parameters to the function retain_graph=True, You can run back propagation twice .
3. In the case of control flow , We calculated d About a The derivative of , If we put variables a Change to random vector or matrix , What's going to happen ？
   A runtime error has occurred , stay Pytorch in , Don't let the tensor derive from the tensor , Only scalar derivatives of tensors are allowed . If you want to call on a non scalar backward(), You need to pass in a gradient Parameters .
4. Redesign an example of finding the gradient of control flow , Run and analyze the results .

# When  a  The norm of is greater than 10 when , Gradient for all elements is  1  Vector ; When  a  The gradient of is not greater than  10  when , Gradient for all elements is  2  Vector .
def f(a):
    if a.norm() > 10:
        b = a
    else:
        b = 2 * a
    return b.sum()

a = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0], requires_grad=True)
d = f(a)
d.backward()

6. send $f(x)=\sin (x)$, draw $f(x)$ and $\frac{df(x)}{dx}$ Image , The latter does not use $f^{\prime }(x)=\cos (x)$.

The latter does not use $f^{\prime }(x)=\cos (x)$, The original intention of this problem is to save all the derivative values obtained from the derivation of the function , According to these saved df value , Draw $f^{\prime }(x)$

# Import the corresponding library 
import numpy as np
import torch
import matplotlib.pyplot as plt

# Make some definitions 
x = np.arange(-5, 5, 0.02)# Define the argument in [5,5] Between , Every number interval 0.02
f = np.sin(x)
df = []

for i in x:
  # Yes x Find the derivative for every value of 
  v = torch.tensor(i,requires_grad=True)
  y = torch.sin(v)
  y.backward()
  df.append(v.grad)
# The drawing part 
# Create plots with pre-defined labels.
fig, ax = plt.subplots()
ax.plot(x, f, 'k', label='f(x)')
ax.plot(x, df, 'k*', label='df(x)')

legend = ax.legend(loc='upper left', shadow=True, fontsize='x-large')

# Put a nicer background color on the legend.
legend.get_frame().set_facecolor('C0')

plt.show()

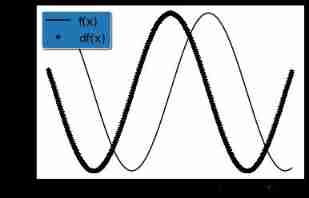
Reference material

Refer to the post