当前位置:网站首页>[combinatorial mathematics] binomial theorem and combinatorial identity (binomial theorem | three combinatorial identities | recursive formula 1 | recursive formula 2 | recursive formula 3 Pascal / Ya
[combinatorial mathematics] binomial theorem and combinatorial identity (binomial theorem | three combinatorial identities | recursive formula 1 | recursive formula 2 | recursive formula 3 Pascal / Ya
2022-07-03 15:20:00 【Programmer community】
List of articles
- One 、 binomial theorem
- Two 、 Combinatorial identity ( recursion 1 )
- 3、 ... and 、 Combinatorial identity ( recursion 2 )
- Four 、 Combinatorial identity ( recursion 3 ) Pascal / Yang Hui's trigonometric formula
- 5、 ... and 、 Combination analysis method
- 6、 ... and 、 Characteristics of recursive combinatorial identities
One 、 binomial theorem
binomial theorem :
n
n
n It's a positive integer. , For everything
x
x
x and
y
y
y , There are the following theorems :
(
x
+
y
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
y
n
−
k
(x + y)^n = \sum_{k=0}^n \dbinom{n}{k}x^k y^{n-k}
(x+y)n=k=0∑n(kn)xkyn−k
(
n
k
)
\dbinom{n}{k}
(kn) Express
n
n
n Yuan centralized retrieval
k
k
k Number of combinations of elements , yes Number of sets
C
(
n
,
k
)
C(n,k)
C(n,k) Another way of writing ;
Another common form (
y
=
1
y = 1
y=1 ) :
(
1
+
x
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
(1 + x)^n = \sum_{k=0}^n \dbinom{n}{k}x^k
(1+x)n=k=0∑n(kn)xk
Basic summation formula (
x
=
y
=
1
x = y =1
x=y=1 ) :
2
n
=
∑
k
=
0
n
(
n
k
)
2^n = \sum_{k=0}^n \dbinom{n}{k}
2n=k=0∑n(kn)
Two 、 Combinatorial identity ( recursion 1 )
(
n
k
)
=
(
n
n
−
k
)
\dbinom{n}{k} = \dbinom{n}{n-k}
(kn)=(n−kn)
Combination analysis method :
(
n
k
)
\dbinom{n}{k}
(kn) Is to seek
k
k
k Subset selection method ,
(
n
n
−
k
)
\dbinom{n}{n-k}
(n−kn) Is to seek
n
−
k
n-k
n−k Selection method of subset , There is a one-to-one correspondence between the two ;
In general ,
(
n
k
)
\dbinom{n}{k}
(kn) Next item of , Not more than half of the above ;
If appear
(
10
8
)
\dbinom{10}{8}
(810) , I can write this as
(
10
2
)
\dbinom{10}{2}
(210)
3、 ... and 、 Combinatorial identity ( recursion 2 )
(
n
k
)
=
n
k
(
n
−
1
k
−
1
)
\dbinom{n}{k} = \dfrac{n}{k} \dbinom{n - 1}{k - 1}
(kn)=kn(k−1n−1)
The formula of substituting the combinatorial number , You can get Equal sign
=
=
= The values on both sides are equal ;
This formula is used to eliminate the coefficient , Examples are as follows :
Calculation
∑
k
=
0
n
k
(
n
k
)
\sum\limits_{k=0}^n k\dbinom{n}{k}
k=0∑nk(kn) combined :
At this time, it needs to be eliminated
k
k
k coefficient ;
Use
n
k
(
n
−
1
k
−
1
)
\dfrac{n}{k} \dbinom{n - 1}{k - 1}
kn(k−1n−1) Instead of
(
n
k
)
\dbinom{n}{k}
(kn) , There is the following calculation process :
∑
k
=
0
n
k
(
n
k
)
=
∑
k
=
0
n
k
n
k
(
n
−
1
k
−
1
)
\begin{array}{lcl} \sum\limits_{k=0}^n k\dbinom{n}{k} = \sum\limits_{k=0}^n k \dfrac{n}{k} \dbinom{n - 1}{k - 1} \end{array}
k=0∑nk(kn)=k=0∑nkkn(k−1n−1)
You can add
k
k
k About , here
n
n
n It has nothing to do with summing variables , Now you can put
n
n
n Extract the addition symbol
∑
\sum
∑ outside ,
∑
k
=
0
n
k
(
n
k
)
=
∑
k
=
0
n
k
n
k
(
n
−
1
k
−
1
)
=
n
∑
k
=
0
n
(
n
−
1
k
−
1
)
\begin{array}{lcl} \sum\limits_{k=0}^n k\dbinom{n}{k} &=& \sum\limits_{k=0}^n k \dfrac{n}{k} \dbinom{n - 1}{k - 1} \\\\ &=& n \sum\limits_{k=0}^n \dbinom{n - 1}{k - 1} \end{array}
k=0∑nk(kn)==k=0∑nkkn(k−1n−1)nk=0∑n(k−1n−1)
And then calculate
∑
k
=
0
n
(
n
−
1
k
−
1
)
\sum\limits_{k=0}^n \dbinom{n - 1}{k - 1}
k=0∑n(k−1n−1) ,
Binomial theorem is :
(
x
+
y
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
y
n
−
k
(x + y)^n = \sum_{k=0}^n \dbinom{n}{k}x^k y^{n-k}
(x+y)n=k=0∑n(kn)xkyn−k
According to the binomial theorem , You can get
(
1
+
1
)
n
=
∑
k
=
0
n
(
n
k
)
(1 + 1)^{n} = \sum\limits_{k=0}^n \dbinom{n}{k}
(1+1)n=k=0∑n(kn)
deduction :
(
1
+
1
)
n
−
1
=
∑
k
=
0
n
−
1
(
n
−
1
k
−
1
)
=
2
n
−
1
(1 + 1)^{n-1} = \sum\limits_{k=0}^{n-1} \dbinom{n-1}{k-1} = 2^{n-1}
(1+1)n−1=k=0∑n−1(k−1n−1)=2n−1
Then you can continue the subsequent calculation ;
Four 、 Combinatorial identity ( recursion 3 ) Pascal / Yang Hui's trigonometric formula
(
n
k
)
=
(
n
−
1
k
)
+
(
n
−
1
k
−
1
)
\dbinom{n}{k} = \dbinom{n - 1}{k} + \dbinom{n - 1}{k - 1}
(kn)=(kn−1)+(k−1n−1)
This recursion , Used to split items :
Can be
(
n
k
)
\dbinom{n}{k}
(kn) Split into
(
n
−
1
k
)
+
(
n
−
1
k
−
1
)
\dbinom{n - 1}{k} + \dbinom{n - 1}{k - 1}
(kn−1)+(k−1n−1) The sum of the ;
take
(
n
−
1
k
)
\dbinom{n - 1}{k}
(kn−1) Split into
(
n
k
)
−
(
n
−
1
k
−
1
)
\dbinom{n}{k} -\dbinom{n - 1}{k - 1}
(kn)−(k−1n−1) The difference between the ;
take take
(
n
−
1
k
−
1
)
\dbinom{n - 1}{k - 1}
(k−1n−1) Split into
(
n
k
)
−
(
n
−
1
k
)
\dbinom{n}{k} -\dbinom{n - 1}{k}
(kn)−(kn−1) The difference between the ;
In a stack of summation combinatorial numbers , Split into the difference between two numbers , Can offset many combinations ;
It is often used for simplification in large sum formulas ;
The formula is proved by using the method of combinatorial analysis :
take
n
n
n Meta set selection
k
k
k A subset of , This is the number of set combinations ;
Specify one of the elements
a
a
a ;
① contain
a
a
a Elements :
k
k
k The subset contains
a
a
a The number of combinations of elements by
(
n
−
1
k
−
1
)
\dbinom{n - 1}{k - 1}
(k−1n−1) ,
k
k
k The subset contains
a
a
a , Just divide
a
a
a Out of element , The rest
n
−
1
n-1
n−1 Of the elements , elect
k
−
1
k-1
k−1 Just one element ;
② It doesn't contain
a
a
a Elements :
k
k
k Subset does not contain
a
a
a The number of combinations of elements by
(
n
−
1
k
)
\dbinom{n - 1}{k}
(kn−1) ,
k
k
k Subset does not contain
a
a
a , Just divide
a
a
a Out of element , The rest
n
−
1
n-1
n−1 Of the elements , elect
k
k
k Just one element ;
5、 ... and 、 Combination analysis method
Prove with the above Pascal / Yang hui triangle Take the formula as an example
The combination analysis method uses : When using the combination analysis method to prove the combination number , Specify the set first , Specify elements , Specify two counting problems , On both sides of the formula are the counts of the same problem ;
- Specify the collection :
n
n
n Meta set
- Specify elements : A particular element
a
a
a
- Specify the counting problem :
- ① problem 1 :
n
n
n Meta set
k
k
k Combinatorial number ;
- ② problem 2 :
n
n
n Yuanji
k
k
k Combinatorial number , The combination contains elements
a
a
a , No elements
a
a
a Two combined counts of ;
- ① problem 1 :
6、 ... and 、 Characteristics of recursive combinatorial identities
Use A relatively small number of combinations Express Relatively large number of combinations , It is called recursive combinatorial identity ;
边栏推荐
- Leetcode sword offer find the number I (nine) in the sorted array
- Matlab r2011b neural network toolbox precautions
- Besides lying flat, what else can a 27 year old do in life?
- Jvm-05-object, direct memory, string constant pool
- 百度智能云助力石嘴山市升级“互联网+养老服务”智慧康养新模式
- Global and Chinese markets for flexible chips 2022-2028: Research Report on technology, participants, trends, market size and share
- Redis cache penetration, cache breakdown, cache avalanche solution
- Using Tengine to solve the session problem of load balancing
- Global and Chinese market of marketing automation 2022-2028: Research Report on technology, participants, trends, market size and share
- Tensorflow realizes verification code recognition (II)
猜你喜欢

Influxdb2 sources add data sources

qt使用QZxing生成二维码

什么是one-hot encoding?Pytorch中,将label变成one hot编码的两种方式
Can‘t connect to MySQL server on ‘localhost‘

Jvm-05-object, direct memory, string constant pool
Summary of JVM knowledge points

百度智能云助力石嘴山市升级“互联网+养老服务”智慧康养新模式
视觉上位系统设计开发(halcon-winform)-5.相机

【注意力机制】【首篇ViT】DETR,End-to-End Object Detection with Transformers网络的主要组成是CNN和Transformer
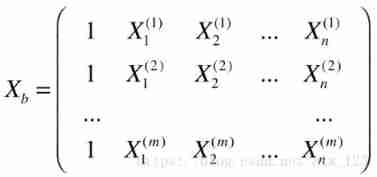
Popular understanding of linear regression (II)
随机推荐
Summary of concurrent full knowledge points
Jvm-04-runtime data area heap, method area
【pytorch学习笔记】Datasets and Dataloaders
Kubernetes will show you from beginning to end
[pytorch learning notes] transforms
使用Tengine解决负载均衡的Session问题
Enable multi-threaded download of chrome and edge browsers
Halcon与Winform学习第一节
视觉上位系统设计开发(halcon-winform)-5.相机
Functional modules and application scenarios covered by the productization of user portraits
Explanation of time complexity and space complexity
Concurrency-01-create thread, sleep, yield, wait, join, interrupt, thread state, synchronized, park, reentrantlock
[transform] [NLP] first proposed transformer. The 2017 paper "attention is all you need" by Google brain team
mysql innodb 存储引擎的特性—行锁剖析
百度智能云助力石嘴山市升级“互联网+养老服务”智慧康养新模式
Construction of operation and maintenance system
Popular understanding of linear regression (II)
Global and Chinese markets for infrared solutions (for industrial, civil, national defense and security applications) 2022-2028: Research Report on technology, participants, trends, market size and sh
[transform] [practice] use pytoch's torch nn. Multiheadattention to realize self attention
qt使用QZxing生成二维码