[factorial inverse], [linear inverse], [combinatorial counting] Niu Mei's mathematical problems

️ Pre knowledge ️

1️⃣ Introduction to inverse element

$a\times b\equiv 1(modp)$, It can be said that a yes b In the mold p Inverse element in case .
In fact, the inverse element can be regarded as the reciprocal

2️⃣ Factorial inverse

Mode one :
Find the inverse element through Fermat's theorem ：
When p As a prime number , also gcd(a,p)=1 when , We have $a^{p-1}\equiv 1(modp)$. Then there is $a^{p-2}\times a\equiv 1(modp)$, be a The inverse of is $a^{p-2}$
below ksm The function is a fast power

fact[0] = 1;
for(int i = 1; i < N; i++)
{
    
	fact[i] = fact[i - 1] * i % mod;
	inv[i] = ksm(fact[i], mod - 2);
}

---

Mode two ：

Pass formula $\frac{1}{(n+1)!}\times (n+1)=\frac{1}{n!}$ The inverse element of factorial is deduced from the approximate linearity

$\frac{1}{(n+1)!}$ In fact, it can be seen as $(n+1)!$ Inverse element

for(int i = 1; i <= n; i++)
	fact[i] = fact[i - 1] * i % mod;
inv[n] = ksm(fact[n], mod - 2);
for(int i = n - 1; i >= 1; i--)
	inv[i] = inv[i + 1] * (i + 1) % mod;

---

3️⃣ Linear inverse element

seek $[1,N-1]$ About mod Inverse element time of , It can be done in $O(N)$ Solve in time

Let the modulus be p
For the present i, set up $p=k\times i+r$, be

$\begin{array}{rlr}k\times i+r& \equiv 0& (modp)\\ k\times i\times (i^{-1}\times r^{-1})+r\times (i^{-1}\times r^{-1})& \equiv 0& (modp)\\ k\times r^{-1}+i^{-1}& \equiv 0& (modp)\\ i^{-1}& \equiv -k\times r^{-1}& (modp)\\ i^{-1}& \equiv -\lfloor \frac{p}{i}\rfloor \times r^{-1}& (modp)\end{array}$
Be careful ：
$inv[1]$ Be sure to initialize to 1, Need from 2 Start tweeting , Cannot from 1 Start tweeting

inv[0] = inv[1] = 1;
for(int i = 2; i < N; i++)
	inv[i] = inv[mod % i] * (mod - mod / i) % mod;

At the same time, we can find Factorial inverse ：
Just multiply the inverse element in a form similar to factorial , Obtained inv[i] That is to say $i!$ Inverse element

for(int i = 2; i < N; i++)
	inv[i] = inv[i - 1] * inv[i] % mod;

---

4️⃣ Combination number calculation

$C_n^m$ Calculation
️ Mode one ： Formula calculation
Calculations are based on inverse elements or factorials
$C_n^m=\frac{n!}{m!\ast (n-m)!}$

ll C(ll n, ll m)
{
    
	if(n < m) return 0;
	return fact[n] * inv[m] % mod * inv[n - m] % mod;
}

️ Mode two ： Recursive method
Table creation required , Therefore, if the calculation range is relatively large, the space required is also large
The recursive formula ： $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$

for(int i = 1; i <= n; i++)
	for(int j = 0; j <= i; j++)
	{
    
		if(i == j || j == 0) c[i][j] = 1;
		else c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
	}

---

5️⃣ subject

link ：
https://ac.nowcoder.com/acm/contest/23481/J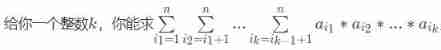

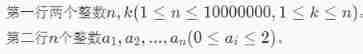
Is to select k Multiply values , Finally, add the results

---

Because there are only three cases of the number size in the array . So you can cut the entrance according to this .

First $0$ You don't have to think about , Next, consider $n$ individual $1$ and $m$ individual $2$, If the sum above $1$ There is $i$ individual , that $2$ There needs to be $k-i$ individual , So the answer is ${\sum }_{i=0}^{k}C(n,i)\ast C(m,k-i)\ast 2^{k-i}$

---

Pay attention to various initializations in the code
Initialization in linear inverse ：inv[1] = 1
fac[i]:$2^i$
fact[i]:$i!$

#include<bits/stdc++.h>
using namespace std;

using ll = long long;
const int N = 1e7 + 5, mod = 998244353;

ll fac[N], fact[N], inv[N];

ll C(ll n, ll m)
{
    
	if(n < m) return 0;
	return fact[n] * inv[m] % mod * inv[n - m] % mod;
}

void solve()
{
    
	fac[1] = 2;
	fac[0] = fact[0] = fact[1] = inv[0] = inv[1] = 1;
	for(int i = 2; i < N; i++)
	{
    
		fac[i] = fac[i - 1] * 2 % mod;
		fact[i] = fact[i - 1] * i % mod;
		inv[i] = inv[mod % i] * (mod - mod / i) % mod; 
	}
	for(int i = 2; i < N; i++)
		inv[i] = inv[i - 1] * inv[i] % mod;
		
	int n, k;
	cin >> n >> k;
	vector<int> a(n);
	int o = 0, t = 0;
	
	for(int i = 0; i < n; i++) 
	{
    
		cin >> a[i];
		if(a[i] == 1) o ++;
		else if(a[i] == 2) t ++;
	}	
	ll res = 0;
	for(int i = 0; i <= k; i++)
	{
    
		res += C(o, i) * C(t, k - i) % mod * fac[k - i] % mod;
		res %= mod;
	}
	cout << res << "\n";
}
int main()
{
    
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t;
// cin >> t;
	t = 1;
	while(t--) solve();
	return 0;
}