当前位置:网站首页>【机器人坐标系第一讲】
【机器人坐标系第一讲】
2022-07-05 16:14:00 【小秋SLAM实战教程】
// 求解的是世界坐标系到相机坐标系的变换矩阵
cv::Mat Tcw = mpTracker->GrabImageRGBD(im,depthmap,timestamp);
// 保存轨迹是相机坐标系到世界坐标系的变换矩阵
// 将相机坐标系下面的点装换到世界坐标系下面
mRcw = mTcw.rowRange(0,3).colRange(0,3);
mRwc = mRcw.t();
mRwc * x3Dc + -mRwc*mTcw.rowRange(0,3).col(3);

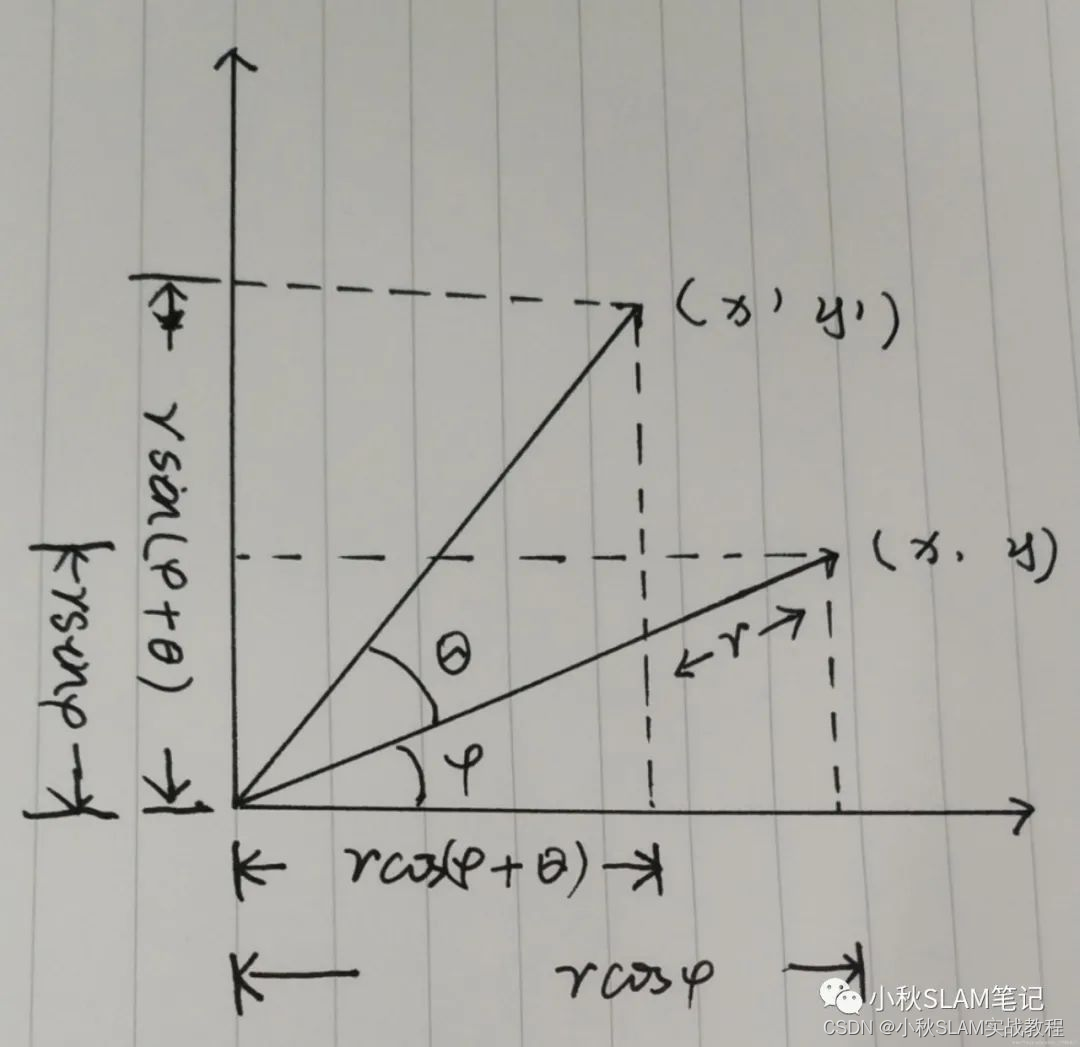 角度要是负数,右手法则
角度要是负数,右手法则


机器人坐标系 符合右手坐标系 红前x 绿左y 蓝上z
x+ to forward, y+ to left, z+ to up
q.setRPY(0, M_PI/2, -M_PI/2); // -0 90 -90 先绕z轴负90度 再绕y轴正90度 最后绕x轴转0度
// 旋转矩阵
Eigen::Matrix3d rotation_matrix3d;
// 绕 Z 轴旋转 45 度的旋转矩阵 sin45 = cos45 = 0.707107
rotation_matrix3d << cos45, -sin45, 0,
sin45, cos45, 0,
0, 0, 1;
rotation_matrix3d << 0.707107, -0.707107, 0,
0.707107, 0.707107, 0,
0, 0, 1;
std::cout << "rotation_matrix =\n" << rotation_matrix << std::endl;
/* * rotation_matrix = * 0.707107 -0.707107 0 * 0.707107 0.707107 0 * 0 0 1 */
// 2. 旋转矩阵转换为欧拉角,"2" represents the z axis , "0" x axis, "1" y axis
Eigen::Vector3d euler_angle = rotation_matrix3d.eulerAngles(2, 1, 0);// z y x
std::cout << "绕z轴旋转的角度是 " << euler_angle.z() * 180 / M_PI << std::endl;
std::cout << "绕y轴旋转的角度是 " << euler_angle.y() * 180 / M_PI << std::endl;
std::cout << "绕x轴旋转的角度是 " << euler_angle.x() * 180 / M_PI << std::endl;
tf_camera_rotation.getEulerYPR(z,y,x);
std::cout << "zb " << z << " yb " << y << " xb " << x << std::endl; // rotation_matrix3d.x() -1.57062 rotation_matrix3d.y() -0.000116255 rotation_matrix3d.z() -1.57072
边栏推荐
猜你喜欢
Win11提示无法安全下载软件怎么办?Win11无法安全下载软件
BS-XX-042 基于SSM实现人事管理系统

Reduce the cost by 40%! Container practice of redis multi tenant cluster

2020-2022两周年创作纪念日
HiEngine:可媲美本地的云原生内存数据库引擎

Global Data Center released DC brain system, enabling intelligent operation and management through science and technology
Flet教程之 11 Row组件在水平数组中显示其子项的控件 基础入门(教程含源码)
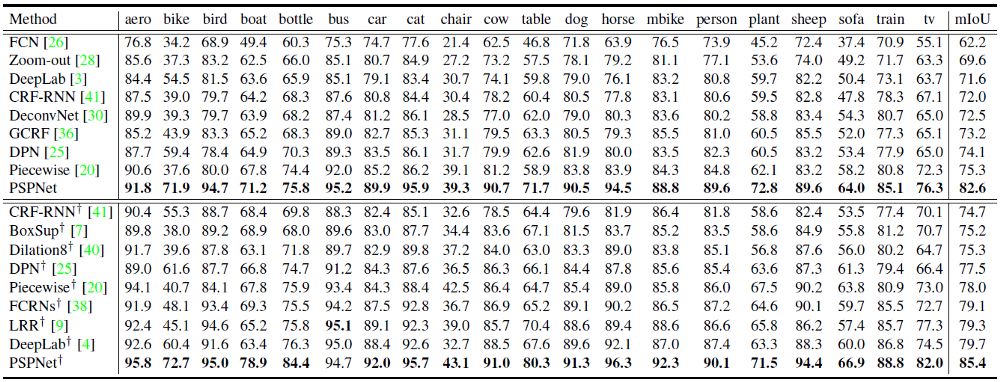
PSPNet | 语义分割及场景分析
Games101 notes (II)

【 brosser le titre 】 chemise culturelle de l'usine d'oies
随机推荐
tf.sequence_mask函数讲解案例
自己要有自己的坚持
Summary of PHP pseudo protocol of cisp-pte
【729. 我的日程安排表 I】
Single merchant v4.4 has the same original intention and strength!
How to set the WiFi password of the router on the computer
How to install MySQL
Apple has abandoned navigationview and used navigationstack and navigationsplitview to implement swiftui navigation
Jarvis OJ shell traffic analysis
"21 days proficient in typescript-3" - install and build a typescript development environment md
StarkWare:欲构建ZK“宇宙”
SQL injection of cisp-pte (Application of secondary injection)
解决CMakeList find_package找不到Qt5,找不到ECM
Dare not buy thinking
Fleet tutorial 09 basic introduction to navigationrail (tutorial includes source code)
Bs-xx-042 implementation of personnel management system based on SSM
Android privacy sandbox developer preview 3: privacy, security and personalized experience
Explain in detail the functions and underlying implementation logic of the groups sets statement in SQL
[61dctf]fm
Facing new challenges and becoming a better self -- attacking technology er