当前位置:网站首页>Bipartite graph determination
Bipartite graph determination
2022-07-06 22:47:00 【AC__ dream】
First, let's talk about what is a bipartite graph , For a picture , We divide its vertex set into two parts A and B, Thus, one of the two vertices of any edge is A One of them is in B in , Instead of having two vertices of an edge all in A In or all of B In this case .
Let's start with a theorem : A graph is a bipartite graph if and only if there are no odd rings in this graph , That is, there is no ring with an odd number of vertices .
If we use this theorem to determine whether a graph is a bipartite graph, then we can use the method of coloring to realize , The color of the two vertices of each edge must be different , We dye the graph according to this principle , If the coloring is successful, then this graph is a bipartite graph , Otherwise, it is not a bipartite graph .
Give an example and its code implementation :

sample input :
4 4
1 3
1 4
2 3
2 4sample output :
YesCode :
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
using namespace std;
const int N=2e5+10;
int h[N],e[N],ne[N],color[N],idx;
//color[i] On behalf of the i Color of nodes
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
bool dfs(int x,int c)
{
color[x]=c;
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(color[j]!=-1)//j Nodes have been dyed
{
if(color[j]==c) return false;// Two vertices of an edge have the same color , contradiction
}
else if(!dfs(j,c^1)) return false;// Find contradictions
}
return true;// All nodes return true without finding contradictions
}
int main()
{
int n,m;
cin>>n>>m;
memset(h,-1,sizeof h);
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
memset(color,-1,sizeof color);// The initial color is -1
bool flag=true;
for(int i=1;i<=n;i++)
{
if(color[i]==-1)
{
if(!dfs(i,1))// Dye the current dot into 1 Number color
{
flag=false;// Exit directly when there is an odd ring
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}边栏推荐
- BasicVSR_PlusPlus-master测试视频、图片
- Balanced Multimodal Learning via On-the-fly Gradient Modulation(CVPR2022 oral)
- Aardio - 封装库时批量处理属性与回调函数的方法
- Puppeter connects to the existing Chrome browser
- Aardio - 利用customPlus库+plus构造一个多按钮组件
- Designed for decision tree, the National University of Singapore and Tsinghua University jointly proposed a fast and safe federal learning system
- memcached
- General implementation and encapsulation of go diversified timing tasks
- Volatile keyword
- Is there any requirement for the value after the case keyword?
猜你喜欢
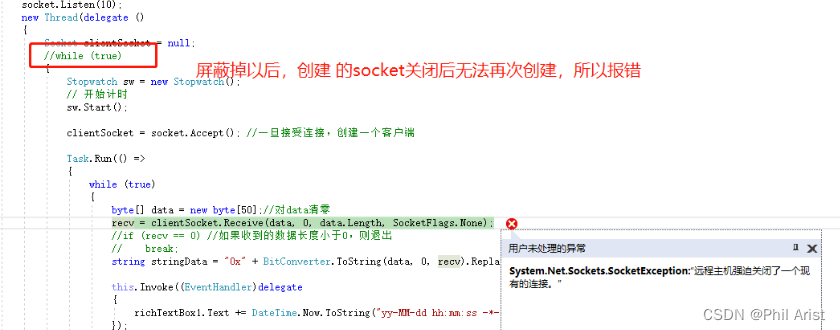
C# 三种方式实现Socket数据接收
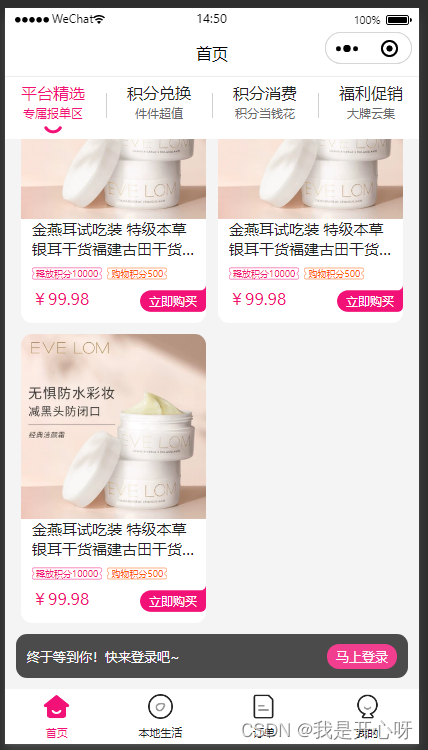
Slide the uniapp to a certain height and fix an element to the top effect demo (organize)
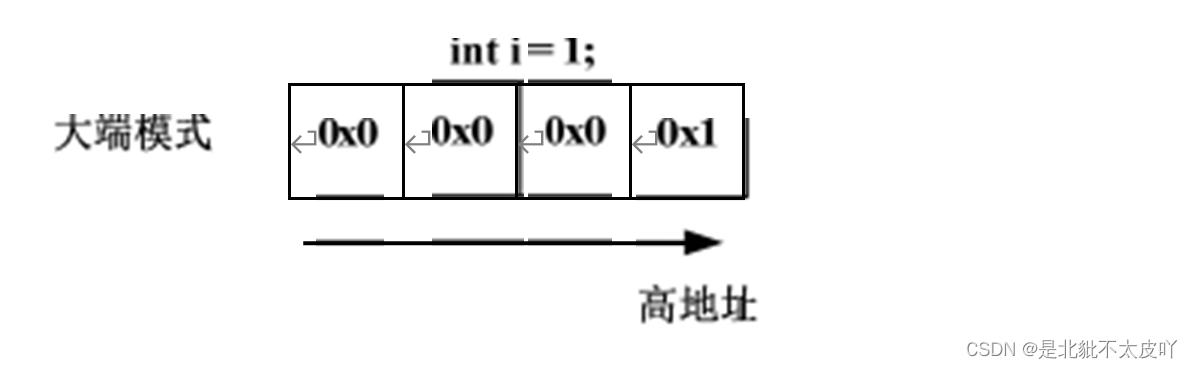
如何用程序确认当前系统的存储模式?
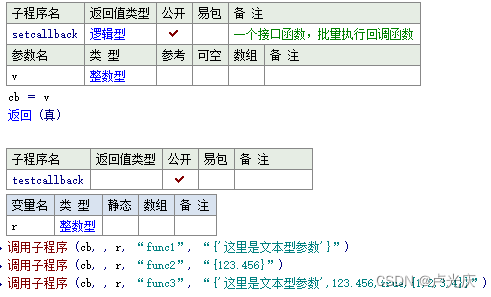
Aardio - Method of batch processing attributes and callback functions when encapsulating Libraries
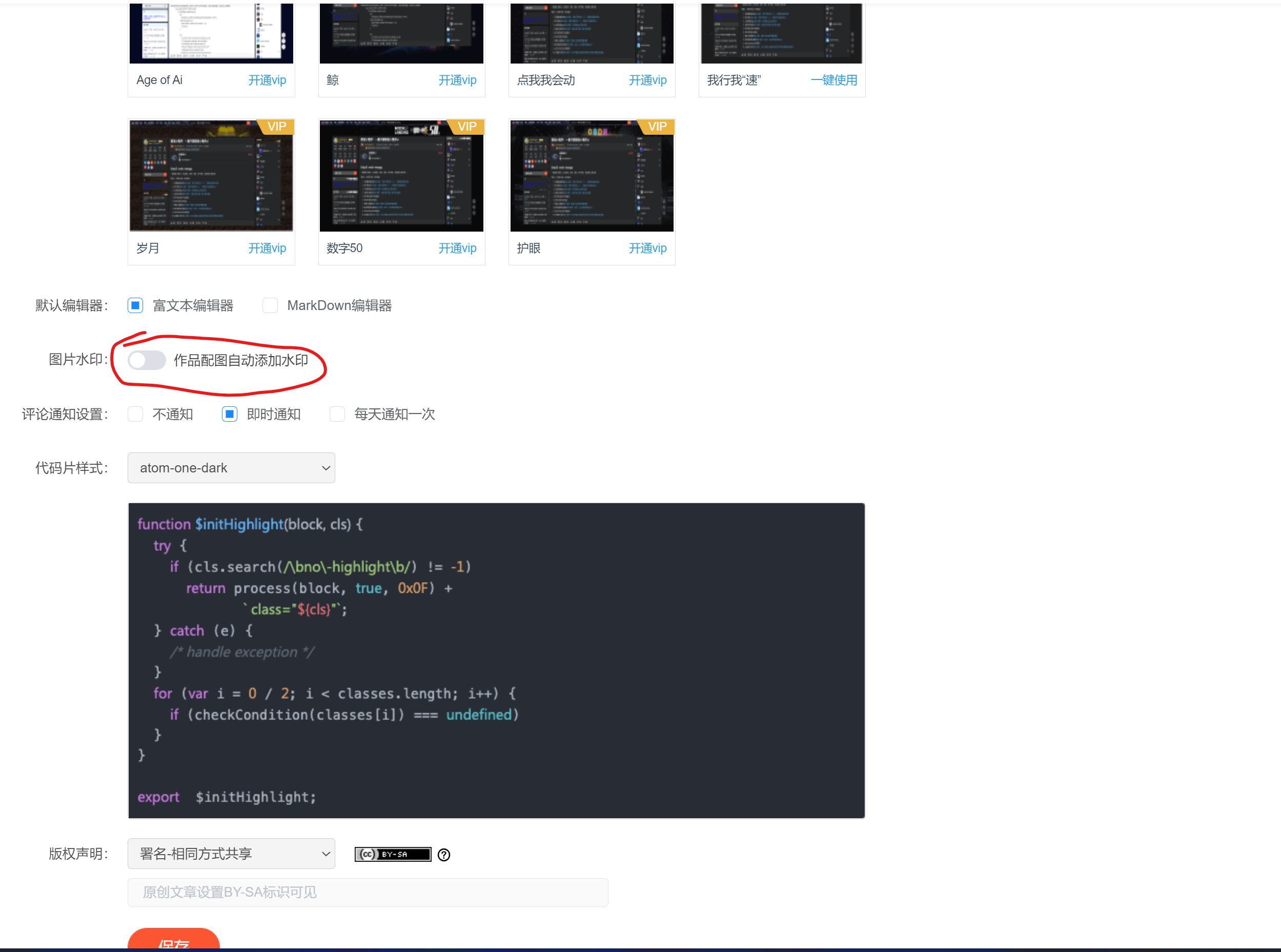
CSDN 上传图片取消自动加水印的方法

新手程序员该不该背代码?

DR-Net: dual-rotation network with feature map enhancement for medical image segmentation
![[leetcode] 19. Delete the penultimate node of the linked list](/img/ab/25cb6d6538ad02d78f7d64b2a2df3f.png)
[leetcode] 19. Delete the penultimate node of the linked list

UE4 blueprint learning chapter (IV) -- process control forloop and whileloop

Web APIs DOM time object
随机推荐
做国外LEAD2022年下半年几点建议
Comparison between variable and "zero value"
[step on pit collection] attempting to deserialize object on CUDA device+buff/cache occupy too much +pad_ sequence
Aardio - Method of batch processing attributes and callback functions when encapsulating Libraries
General implementation and encapsulation of go diversified timing tasks
Senior soft test (Information System Project Manager) high frequency test site: project quality management
Mysql 身份认证绕过漏洞(CVE-2012-2122)
雅思口语的具体步骤和时间安排是什么样的?
Unified Focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medi
Detailed explanation of ThreadLocal
云原生技术--- 容器知识点
Cloud native technology container knowledge points
自定义 swap 函数
UE4蓝图学习篇(四)--流程控制ForLoop和WhileLoop
服务器的系统怎么选者
void关键字
On the problems of born charge and non analytical correction in phonon and heat transport calculations
case 关键字后面的值有什么要求吗?
【雅思口语】安娜口语学习记录part1
NPM cannot install sharp