当前位置:网站首页>Codeworks 5 questions per day (average 1500) - day 8
Codeworks 5 questions per day (average 1500) - day 8
2022-07-07 23:43:00 【Soup key TJ】
Cola
Topic translation
Yes a bottle 0.5 l ,b bottle 1 l ,c bottle 2 Liter coke , Please buy n Number of schemes for liter of coke
Input n n n , a a a , b b b , c c c ( 1 < = n < = 10000 1<=n<=10000 1<=n<=10000 , 0 < = a , b , c < = 5000 0<=a,b,c<=5000 0<=a,b,c<=5000 ).
Title Description
To celebrate the opening of the Winter Computer School the organizers decided to buy in n n n liters of cola.
However, an unexpected difficulty occurred in the shop: it turned out that cola is sold in bottles 0.5 0.5 0.5 , 1 1 1 and 2 2 2 liters in volume.
At that, there are exactly a a a bottles 0.5 0.5 0.5 in volume, b b b one-liter bottles and c c c of two-liter ones.
The organizers have enough money to buy any amount of cola.
What did cause the heated arguments was how many bottles of every kind to buy, as this question is pivotal for the distribution of cola among the participants (and organizers as well).
Thus, while the organizers are having the argument, discussing different variants of buying cola, the Winter School can’t start.
Your task is to count the number of all the possible ways to buy exactly n n n liters of cola and persuade the organizers that this number is too large, and if they keep on arguing, then the Winter Computer School will have to be organized in summer.
All the bottles of cola are considered indistinguishable, i.e. two variants of buying are different from each other only if they differ in the number of bottles of at least one kind.
Input format
The first line contains four integers — n n n , a a a , b b b , c c c ( 1 < = n < = 10000 1<=n<=10000 1<=n<=10000 , 0 < = a , b , c < = 5000 0<=a,b,c<=5000 0<=a,b,c<=5000 ).
Output format
Print the unique number — the solution to the problem.
If it is impossible to buy exactly n n n liters of cola, print 0 0 0 .
Examples #1
The sample input #1
10 5 5 5
Sample output #1
9
Examples #2
The sample input #2
3 0 0 2
Sample output #2
0
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
int n,a,b,c,s=0;
int main(){
cin>>n>>a>>b>>c;
for(int i=0;i<=c&&i*2<=n;i++)
{
int k=n-i*2;
if(k<=b) s+=min(a/2,k)+1;
else
{
if((k-b)*2<=a)
s+=min((a-(k-b)*2)/2,b)+1;
}
}
cout<<s;
return 0;
}
Winner
Topic translation
Title Description :
stay Berland Card games are popular Berlogging, The winner of this game is determined according to the following rules :
- In each round , Players gain or lose a certain number of points , During the game , The score is recorded in
Name and scoreIn line , The name is the player's name , The score is the score obtained in this round . A negative score means that the player loses the corresponding score . - If only one player scores the most at the end of the game , He is the winner .
- If two or more players have the highest score at the end of the game m m m , Then first of all, at least m m m Players with points win . At the beginning of the , Every player is 0 0 0 branch .
Ensure that at least one player has a positive score at the end of the game .
【 Input format 】
The first line contains integers n n n, Indicates the number of rounds of the game .
The first 2 ∼ n + 1 2 \sim n + 1 2∼n+1 That's ok , Enter... In chronological order Name and score All right , Where the name is no longer than 32 32 32 A string of lowercase letters , The absolute value of the score is not greater than 1000 1000 1000.
【 Output format 】
Output the name of the winner .
Title Description
The winner of the card game popular in Berland “Berlogging” is determined according to the following rules.
If at the end of the game there is only one player with the maximum number of points, he is the winner.
The situation becomes more difficult if the number of such players is more than one.
During each round a player gains or loses a particular number of points.
In the course of the game the number of points is registered in the line “name score”, where name is a player’s name, and score is the number of points gained in this round, which is an integer number.
If score is negative, this means that the player has lost in the round.
So, if two or more players have the maximum number of points (say, it equals to m m m ) at the end of the game, than wins the one of them who scored at least m m m points first.
Initially each player has 0 points.
It’s guaranteed that at the end of the game at least one player has a positive number of points.
Input format
The first line contains an integer number n n n ( 1 < = n < = 1000 1<=n<=1000 1<=n<=1000 ), n n n is the number of rounds played.
Then follow n n n lines, containing the information about the rounds in “name score” format in chronological order, where name is a string of lower-case Latin letters with the length from 1 to 32, and score is an integer number between -1000 and 1000, inclusive.
Output format
Print the name of the winner.
Examples #1
The sample input #1
3
mike 3
andrew 5
mike 2
Sample output #1
andrew
Examples #2
The sample input #2
3
andrew 3
andrew 2
mike 5
Sample output #2
andrew
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
map<string,int> a,b;
string s[N],da;
int n,mmax=-INT_MAX,aa[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i]>>aa[i];
a[s[i]]+=aa[i];
}
for(int i=1;i<=n;i++){
mmax=max(mmax,a[s[i]]);
}
for(int i=1;i<=n;i++){
b[s[i]]+=aa[i];
if(b[s[i]]>=mmax&&a[s[i]]==mmax){
da=s[i];
break;
}
}
cout<<da<<endl;
return 0;
}
Traffic Lights
Topic translation
Title Description
A car with v v v The speed of meters per second is determined by A Point heading B spot . This action takes place in X On the shaft .
In the distance A spot d d d There is a traffic light at the place of meters .
from 0 The moment begins , At the first g g g The green light is on in seconds , And then in the next r r r The red light comes on within seconds , Next g g g second , The green light is on , So again and again .
This car can instantly from 0 0 0 Accelerate to v v v , vice versa , You can also get it from v v v Instantly decelerate to 0 0 0 .
The car can pass immediately when the light is green .
If the car arrives at the traffic light at the moment when the red light is on , Then the car can't pass . But if you arrive when the green light is on , You can use the . Car from 0 Always leave A spot .
Without violating the traffic rules , Car from A Point to move to B How long does it take at least ?
Input format :
The first line contains integers l , d , v , g , r l,d,v,g,r l,d,v,g,r ( 1 ≤ l , d , v , g , r ≤ 1000 , d < l 1\leq l,d,v,g,r\leq1000,d<l 1≤l,d,v,g,r≤1000,d<l )— A And B Distance between ( rice ),A Distance from traffic lights , The speed of the car , Duration of green light and duration of red light .
Output format :
Output a number — Car from A To B The minimum time required . Your output needs to be no more than 1 0 − 6 10^{-6} 10−6
Title Description
A car moves from point A to point B at speed v v v meters per second.
The action takes place on the X-axis.
At the distance d d d meters from A there are traffic lights.
Starting from time 0, for the first g g g seconds the green light is on, then for the following r r r seconds the red light is on, then again the green light is on for the g g g seconds, and so on.
The car can be instantly accelerated from 0 0 0 to v v v and vice versa, can instantly slow down from the v v v to 0 0 0 .
Consider that it passes the traffic lights at the green light instantly.
If the car approaches the traffic lights at the moment when the red light has just turned on, it doesn’t have time to pass it.
But if it approaches the traffic lights at the moment when the green light has just turned on, it can move.
The car leaves point A at the time 0.
What is the minimum time for the car to get from point A to point B without breaking the traffic rules?
Input format
The first line contains integers l l l , d d d , v v v , g g g , r r r ( 1 < = l , d , v , g , r < = 1000 , d < l 1<=l,d,v,g,r<=1000,d<l 1<=l,d,v,g,r<=1000,d<l ) — the distance between A and B (in meters), the distance from A to the traffic lights, car’s speed, the duration of green light and the duration of red light.
Output format
Output a single number — the minimum time that the car needs to get from point A to point B.
Your output must have relative or absolute error less than 1 0 − 6 10^{-6} 10−6 .
Examples #1
The sample input #1
2 1 3 4 5
Sample output #1
0.66666667
Examples #2
The sample input #2
5 4 3 1 1
Sample output #2
2.33333333
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
map<string,int> a,b;
string s[N],da;
double l,d,v,g,r,t;
int main(){
cin>>l>>d>>v>>g>>r;
t=d/v;
while(t>g+r) t-=g+r;
if(t<g){
printf("%.8lf\n",l/v);
}
else{
printf("%.8lf\n",l/v+(g+r-t));
}
return 0;
}
Sum
Topic translation
Title Description :
Vasya Finally learned the carry system , But he often forgets to write the cardinality of the formula .
There is a , He saw that his notebook said a+b=?, But the cardinality is not specified .
Now? Vasya It is considered that the cardinality of the formula is p.
He knows that the formula is under different cardinal numbers , There will be different results , Even under some cardinal numbers, it is meaningless .
Formula 78+87 The value of in hexadecimal is FF, It is 110, The decimal system is 165, The base of the nine is 176, It doesn't make sense under a smaller base .
Now? ,Vasya Want to know the maximum length of the result of the formula .
We define the length of a number as the number of characters of the number , In different base numbers , The same number has different number lengths .
I / O format
Input format :
All in one line , It contains two numbers a,b.
Output format :
All in one line , The maximum length of the output formula .
Title Description
Vasya studies positional numeral systems.
Unfortunately, he often forgets to write the base of notation in which the expression is written.
Once he saw a note in his notebook saying a + b = ? a+b=? a+b=? , and that the base of the positional notation wasn’t written anywhere.
Now Vasya has to choose a base p p p and regard the expression as written in the base p p p positional notation.
Vasya understood that he can get different results with different bases, and some bases are even invalid.
For example, expression 78 + 87 78+87 78+87 in the base 16 positional notation is equal to F F 16 FF_{16} FF16 , in the base 15 positional notation it is equal to 11 0 15 110_{15} 11015 , in the base 10 one — to 16 5 10 165_{10} 16510 , in the base 9 one — to 17 6 9 176_{9} 1769 , and in the base 8 or lesser-based positional notations the expression is invalid as all the numbers should be strictly less than the positional notation base.
Vasya got interested in what is the length of the longest possible expression value.
Help him to find this length.
The length of a number should be understood as the number of numeric characters in it.
For example, the length of the longest answer for 78 + 87 = ? 78+87=? 78+87=? is 3.
It is calculated like that in the base 15 ( 11 0 15 110_{15} 11015 ), base 10 ( 16 5 10 165_{10} 16510 ), base 9 ( 17 6 9 176_{9} 1769 ) positional notations, for example, and in some other ones.
Input format
The first letter contains two space-separated numbers a a a and b b b ( 1 < = a , b < = 1000 1<=a,b<=1000 1<=a,b<=1000 ) which represent the given summands.
Output format
Print a single number — the length of the longest answer.
Examples #1
The sample input #1
78 87
Sample output #1
3
Examples #2
The sample input #2
1 1
Sample output #2
2
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
int a,b,aa[N],aaa=0,bb[N],bbb=0,mmax=0,cc[N];
int main(){
cin>>a>>b;
while(a){
aa[++aaa]=a%10;
a/=10;
mmax=max(mmax,aa[aaa]);
}
while(b){
bb[++bbb]=b%10;
b/=10;
mmax=max(mmax,bb[bbb]);
}
int s=max(aaa,bbb);
for(int i=1;i<=s;i++){
cc[i]+=aa[i]+bb[i];
if(cc[i]>mmax) cc[i+1]++;
}
if(cc[s+1]) s++;
cout<<s<<endl;
return 0;
}
Permutations
Topic translation
Title Description
“ array ” It refers to a length of n Sequence , And among them 1 To n Each number of happens to appear once . for example ,(1) (4,3,5,1,2) (3,2,1) Are arranged , and (1,1) (4,3,1) (2,3,4) It is not .
Suppose someone takes several permutations ( The length is not necessarily the same ), Put them together and write a series , And upset the sequence .
Your task is to reorganize this sequence into several original permutations ( If possible ).
I / O format
Input format :
The first 1 The row is an integer n(1<=n<=105). The next line is after the disruption n It's an integer , Separated by a space . The numbers in this series are 1 To 105 Within the scope of .
Output format :
If this sequence can be divided into several permutations , And each number in the sequence just belongs to an arrangement , Please write on page 1 Number of row output permutations . The first 2 Yes n Number , Corresponding to a given sequence of numbers n Number : If the first i Element belongs to the 1 Permutation , On the output line i The number is 1, If it belongs to the 2 Permutation , Then the number in its corresponding output is 2, wait . The order of these permutations is irrelevant .
If there are multiple answers , Output any one of them . If there is no answer , In the 1 Line output -1.
explain
In the 1 In the three examples, the array is divided into three permutations :(2,1) (3,2,1,4,5) (1,2). The first 1 The first permutation consists of the first of the original sequence 2 and 4 It's made up of numbers , The first 2 The order consists of 3、5、6、7、9 Elements make up , The first 3 The order consists of 1 and 8 Elements make up . obviously , There are several other ways of grouping .
Title Description
A permutation is a sequence of integers from 1 1 1 to n n n of length n n n containing each number exactly once.
For example, ( 1 ) (1) (1) , ( 4 , 3 , 5 , 1 , 2 ) (4,3,5,1,2) (4,3,5,1,2) , ( 3 , 2 , 1 ) (3,2,1) (3,2,1) are permutations, and ( 1 , 1 ) (1,1) (1,1) , ( 4 , 3 , 1 ) (4,3,1) (4,3,1) , ( 2 , 3 , 4 ) (2,3,4) (2,3,4) are not.
There are many tasks on permutations.
Today you are going to solve one of them.
Let’s imagine that somebody took several permutations (perhaps, with a different number of elements), wrote them down consecutively as one array and then shuffled the resulting array.
The task is to restore the initial permutations if it is possible.
Input format
The first line contains an integer n n n ( 1 < = n < = 1 0 5 1<=n<=10^{5} 1<=n<=105 ).
The next line contains the mixed array of n n n integers, divided with a single space.
The numbers in the array are from 1 1 1 to 1 0 5 10^{5} 105 .
Output format
If this array can be split into several permutations so that every element of the array belongs to exactly one permutation, print in the first line the number of permutations.
The second line should contain n n n numbers, corresponding to the elements of the given array.
If the i i i -th element belongs to the first permutation, the i i i -th number should be 1 1 1 , if it belongs to the second one, then its number should be 2 2 2 and so on.
The order of the permutations’ numbering is free.
If several solutions are possible, print any one of them.
If there’s no solution, print in the first line − 1 -1 −1 .
Examples #1
The sample input #1
9
1 2 3 1 2 1 4 2 5
Sample output #1
3
3 1 2 1 2 2 2 3 2
Examples #2
The sample input #2
4
4 3 2 1
Sample output #2
1
1 1 1 1
Examples #3
The sample input #3
4
1 2 2 3
Sample output #3
-1
Tips
In the first sample test the array is split into three permutations: ( 2 , 1 ) (2,1) (2,1) , ( 3 , 2 , 1 , 4 , 5 ) (3,2,1,4,5) (3,2,1,4,5) , ( 1 , 2 ) (1,2) (1,2) .
The first permutation is formed by the second and the fourth elements of the array, the second one — by the third, the fifth, the sixth, the seventh and the ninth elements, the third one — by the first and the eigth elements.
Clearly, there are other splitting variants possible.
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,mmax=0,a[N],tong[N],s[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
tong[a[i]]++;
mmax=max(mmax,a[i]);
}
for(int i=2;i<=mmax;i++){
if(tong[i]>tong[i-1]){
puts("-1");
return 0;
}
}
cout<<tong[1]<<endl;
for(int i=1;i<=n;i++){
s[a[i]]++;
cout<<s[a[i]]<<" ";
}
return 0;
}
边栏推荐
猜你喜欢
![P1067 [noip2009 popularity group] polynomial output (difficult, pit)](/img/1f/a798879a0d65eccefa339b288f2102.jpg)
P1067 [noip2009 popularity group] polynomial output (difficult, pit)
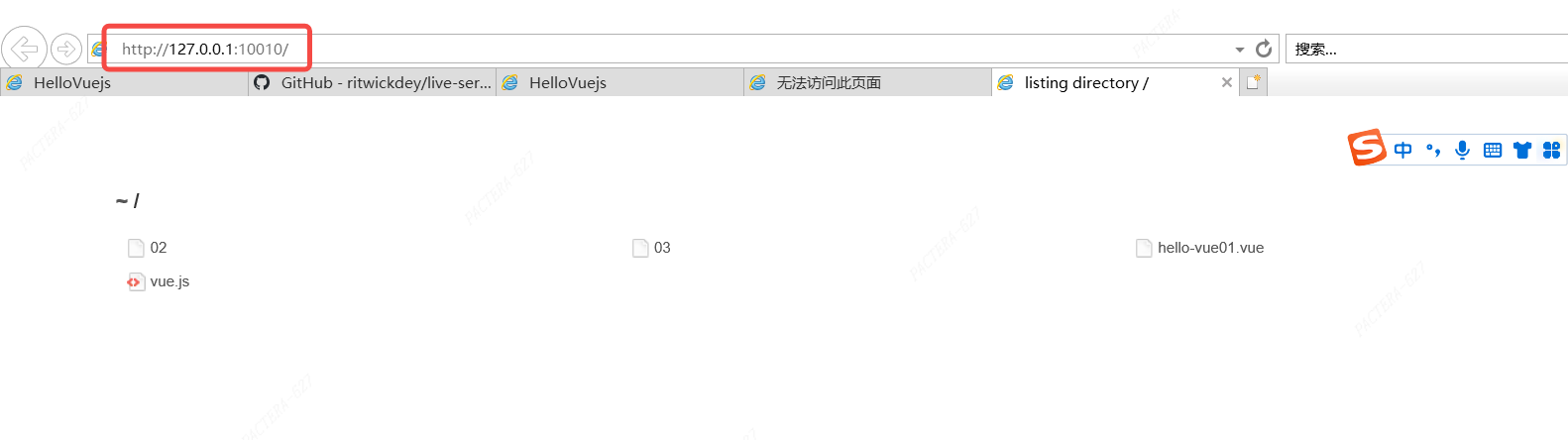
Live server usage

Wechat applet development beginner 1

受限线性表
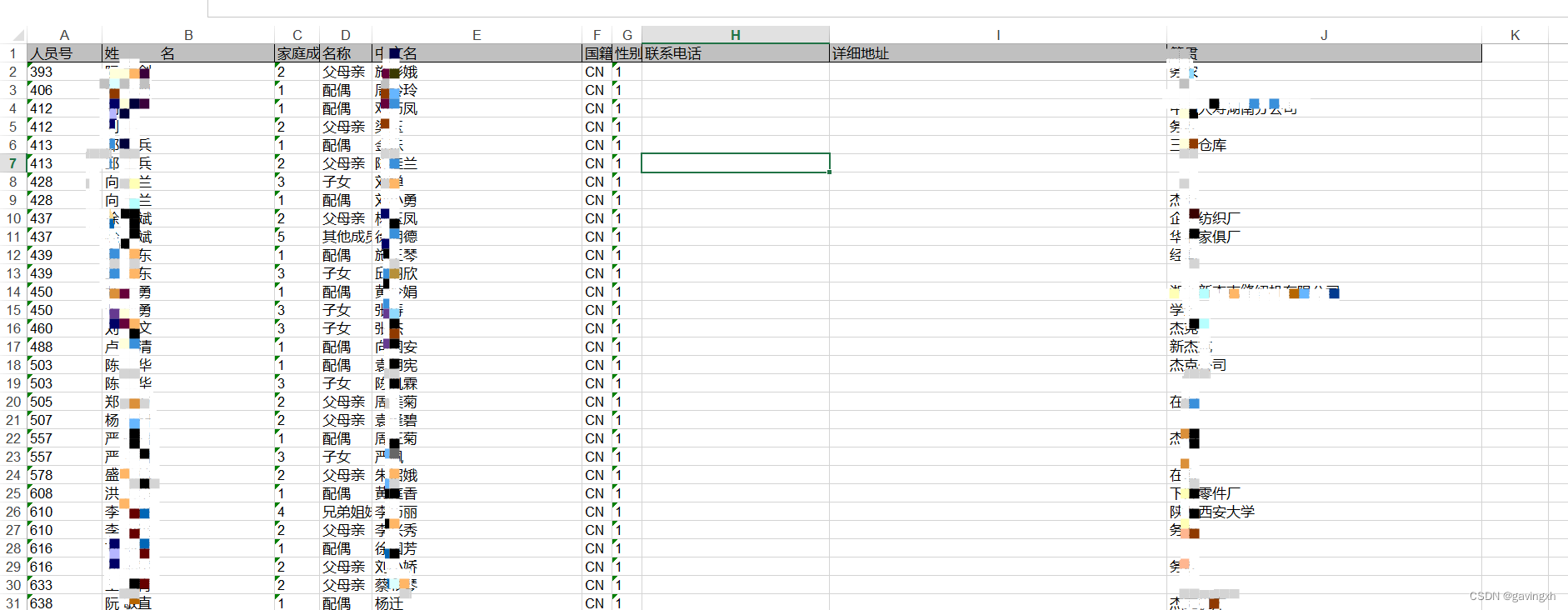
SAP HR 家庭成员信息

神奇快速幂
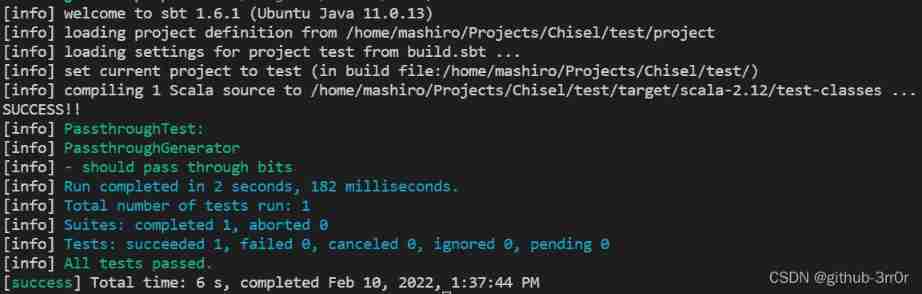
Chisel tutorial - 02 Chisel environment configuration and implementation and testing of the first chisel module
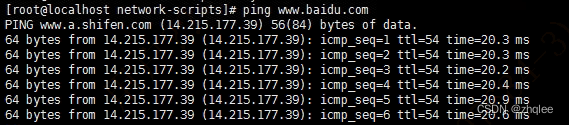
ping报错:未知的名称或服务
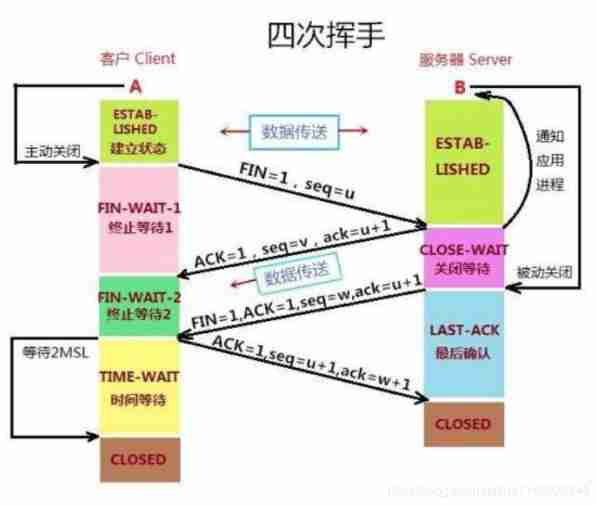
Understand TCP's three handshakes and four waves with love
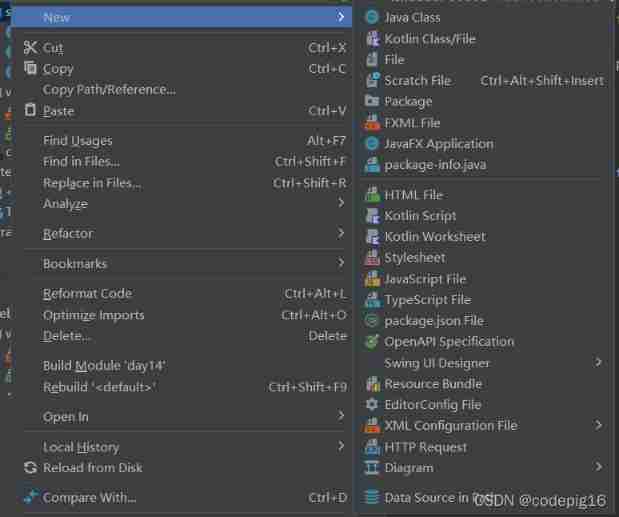
Right click the idea file to create new. There is no solution to create new servlet
随机推荐
@Configuration注解的详细介绍
2022 Season 6 perfect children's model Shaanxi finals came to a successful conclusion
Anti climbing means cracking the second
Svn relocation
网上买基金安全么?
Wechat applet development beginner 1
[stm32+esp8266 connects to Tencent cloud IOT development platform 3] stm32+esp8266-01s dynamically registers devices on Tencent cloud (at instruction mode) -- with source code
关于CH32库函数与STM32库函数的区别
SAP HR social work experience 0023
【路径规划】使用垂距限值法与贝塞尔优化A星路径
【7.4】25. Turn over the linked list in groups of K
C simple question 2
0-1 knapsack problem
Rock-paper-scissors
Dependency injection
P2141 [noip2014 popularization group] abacus mental arithmetic test
Arbre binaire équilibré [Arbre AVL] - Insérer et supprimer
【7.5】15. Sum of three numbers
保证接口数据安全的10种方案
Where are you going