当前位置:网站首页>Eigen sparse matrix operation
Eigen sparse matrix operation
2022-07-06 06:03:00 【Zhan Miao】
In many applications ( for example , The finite element method ), Usually deal with very large matrices , Among them, only a few coefficients are not zero . under these circumstances , You can reduce memory consumption and improve performance by using a dedicated representation that stores only non-zero coefficients . Such a matrix is called sparse matrix .
1. Sparse matrix module
modular | Content | |
#include <Eigen/SparseCore> | SparseMatrix and SparseVector class 、 matrix assemble 、 Basic sparse linear algebra ( Including sparse triangle solver ) | |
#include <Eigen/SparseCholesky> | Directly use sparse LLT and LDLT Cholesky Decomposition to solve the sparse self adjoint positive definite problem | |
#include<Eigen/SparseLU> | sparse LU Decomposition to solve the general square sparse system | |
#include<Eigen/SparseQR | Sparse for solving sparse linear least squares problem QR decompose | |
#include <Eigen/IterativeLinearSolvers> | Iterative solver for solving large general linear square problems ( Including the self adjoint positive definite problem ) | |
#include <Eigen/Sparse> | Including all the above modules |
2. Sparse matrix format
SparseMatrix Class is Eigen The main sparse matrix representation of the sparse module ; It provides high performance and low memory usage . It implements widely used compressed columns ( Or yes ) A more general variant of the storage scheme . It consists of four compact arrays :
Values: Store non-zero coefficient values .
InnerIndices: Store non-zero rows ( Or column ) Indexes .
OuterStarts: For each column ( Or yes ) Store the first non-zero index in the first two arrays .
InnerNNZs: Store each column ( Corresponding line ) Nonzero number of . inner It refers to an internal vector , It is the column of the column master matrix , Or row of the row master matrix . The word external refers to the other direction .
at present , The elements of a given internal vector are always sorted by adding an internal index . “_” Represents the available space to quickly insert new elements . Assume no reallocation , The insertion of random elements is therefore in O(nnz_j) in , among nnz_j Is the nonzero number of the corresponding internal vector . On the other hand , It is more efficient to insert elements with increased internal indexes into a given internal vector , Because this only needs to increase the corresponding InnerNNZs entry , namely O(1) operation .
The case of no available space is a special case , Called compression mode . It corresponds to the widely used compressed column ( Or yes ) Storage plan (CCS or CRS). By calling SparseMatrix::makeCompressed() function , Any SparseMatrix Convert to this form . under these circumstances , It can be noted that InnerNNZs An array with the OuterStarts It's redundant , Because our equation :InnerNNZs[j] = OuterStarts[j+1]-OuterStarts[j]. therefore , Actually call SparseMatrix::makeCompressed() This buffer will be released .
reference
Eigen course 3 - Sparse matrix operation _xuezhisdc The blog of -CSDN Blog _eigen sparse matrix
边栏推荐
- Auto. JS learning notes 17: basic listening events and UI simple click event operations
- CoDeSys note 2: set coil and reset coil
- Station B Liu Erden - linear regression and gradient descent
- 初识数据库
- Expose the serial fraudster Liu Qing in the currency circle, and default hundreds of millions of Cheng Laolai
- Garbage collector with serial, throughput priority and response time priority
- [Baiwen smart home] first day of the course_ Learn Embedded and understand the development mode of bare metal and RTOS
- Analysis of grammar elements in turtle Library
- LTE CSFB process
- High quality coding tool clion
猜你喜欢
Baidu online AI competition - image processing challenge: the 8th program of handwriting erasure
C language bubble sort
![[ram IP] introduction and experiment of ram IP core](/img/34/1c988456e32a8e9840d1d073caefbf.jpg)
[ram IP] introduction and experiment of ram IP core

请求转发与重定向
![Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)](/img/c9/56fba6054c91f090de31463a8b4705.jpg)
Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)
VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
Winter 2021 pat class B problem solution (C language)
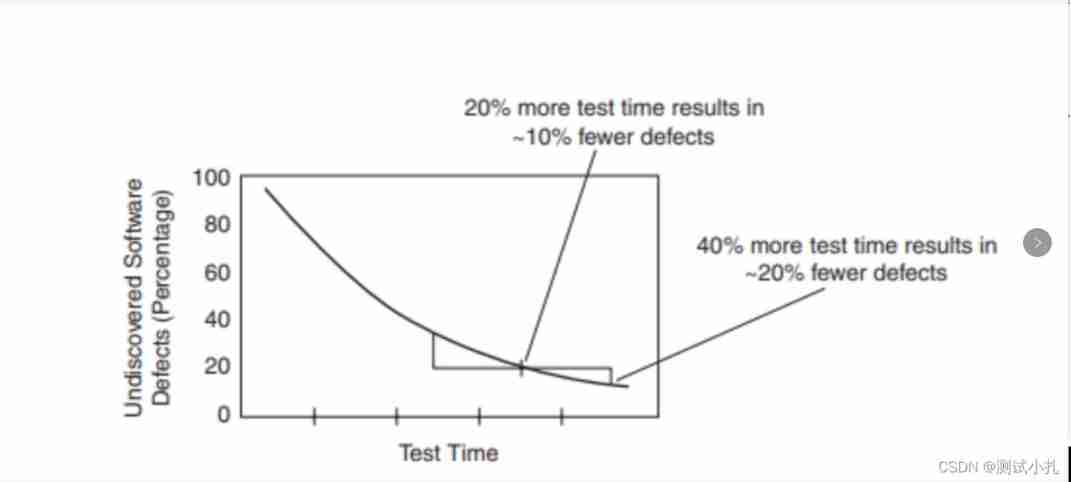
Seven imperceptible truths in software testing
![[Baiwen smart home] first day of the course_ Learn Embedded and understand the development mode of bare metal and RTOS](/img/ed/8d112054f31bd7e593050d1278b9f1.jpg)
[Baiwen smart home] first day of the course_ Learn Embedded and understand the development mode of bare metal and RTOS
SQLMAP使用教程(三)实战技巧二
随机推荐
IDEA 新UI使用
About PHP startup, mongodb cannot find the specified module
Eigen稀疏矩阵操作
AUTOSAR from getting started to becoming proficient (10) - embedded S19 file analysis
Hongliao Technology: how to quickly improve Tiktok store
授予渔,从0开始搭建一个自己想要的网页
isam2运行流程
Station B Liu Erden softmx classifier and MNIST implementation -structure 9
[web security] nodejs prototype chain pollution analysis
J'ai un chaton.
Embedded interview questions (I: process and thread)
Hongliao Technology: Liu qiangdong's "heavy hand"
(5) Explanation of yolo-v3 core source code (3)
Redis6 cluster setup
H3C V7版本交换机配置IRF
ContentType的作用
Wib3.0 leapfrogging, in leapfrogging (ง • ̀_•́) ง
First knowledge database
实践分享:如何安全快速地从 Centos迁移到openEuler
Detailed explanation of BF and KMP