Optimization method of deep learning neural network

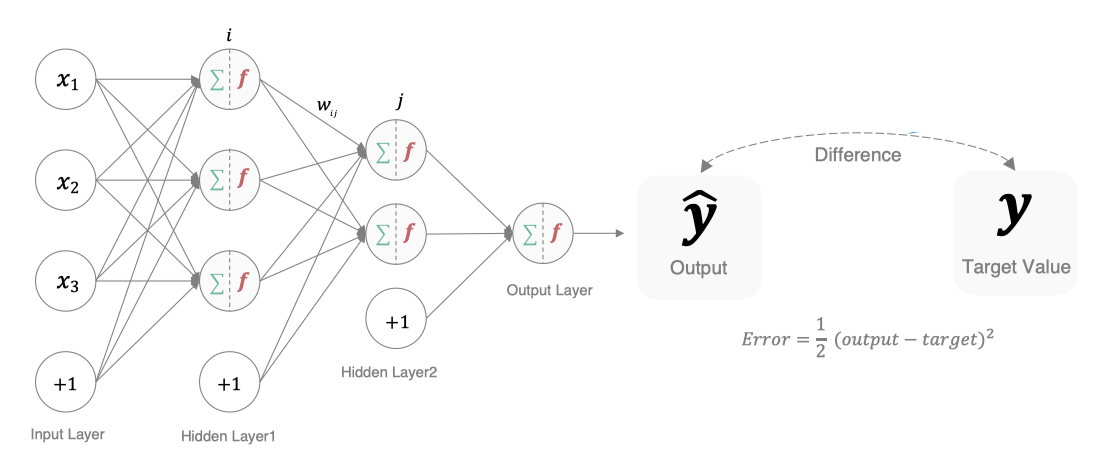
1. Gradient descent algorithm 【 review 】

The gradient descent method is simply a way to find a way to minimize the loss function . You have learned the algorithm in the machine learning stage , So let's simply review here , From a mathematical point of view , The direction of the gradient is the direction where the function grows fastest , So the opposite direction of the gradient is the direction where the function decreases the fastest , So there is ：

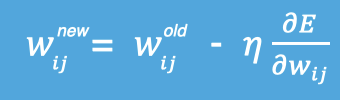
among ,η It's the learning rate , If the learning rate is too small , Then the effect after each training is too small , Increase the time cost of training . If , Learning rate is too high , Then it is possible to skip the optimal solution directly , Enter unlimited training . The solution is , The learning rate also needs to change with the progress of training .

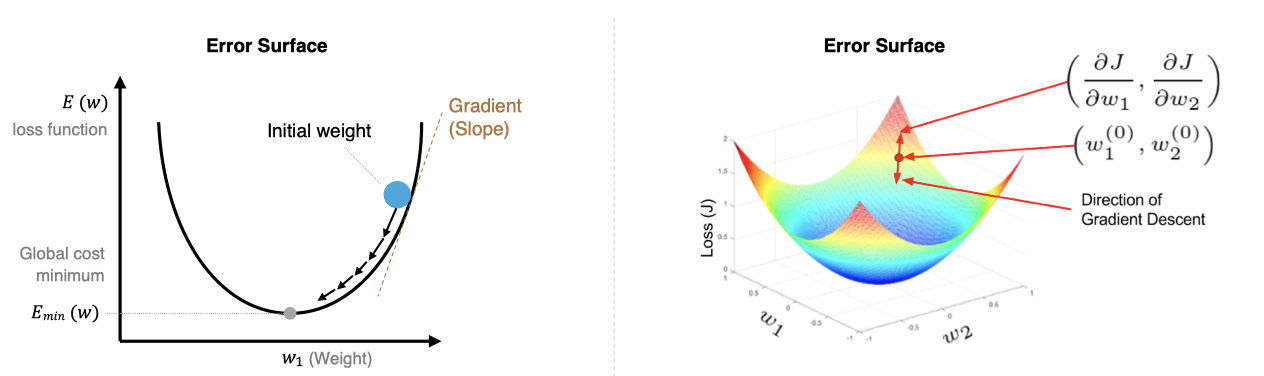
In the figure above, we show one-dimensional and multi-dimensional loss functions , The loss function is in the shape of a bowl . In the training process, the partial derivative of the loss function to the weight is the gradient of the loss function at this position . We can see , Move along the negative gradient , You can reach the bottom of the loss function , Thus minimizing the loss function . The process of using the gradient of the loss function to iteratively find the local minimum is the process of gradient descent .

Based on the sample size used in the iteration , The gradient descent algorithm is divided into the following three categories ：

In practice, the gradient descent algorithm of small batch is often used , stay tf.keras This is achieved in the following ways ：

tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name='SGD', **kwargs
)

Example ：

#  Import the corresponding toolkit 
import tensorflow as tf
#  Instantiate optimization methods ：SGD 
opt = tf.keras.optimizers.SGD(learning_rate=0.1)
#  Define the parameters to be adjusted 
var = tf.Variable(1.0)
#  Define the loss function ： No parameter but return value 
loss = lambda: (var ** 2)/2.0  
#  Calculate the gradient , And update the parameters , In steps of  `- learning_rate * grad`
opt.minimize(loss, [var]).numpy()
#  Display the parameter update results 
var.numpy()

The update result is ：

# 1-0.1*1=0.9
0.9

In model training , There are three basic concepts ：

actually , The fundamental difference between several ways of gradient descent is Batch Size Different ,, As shown in the following table ：

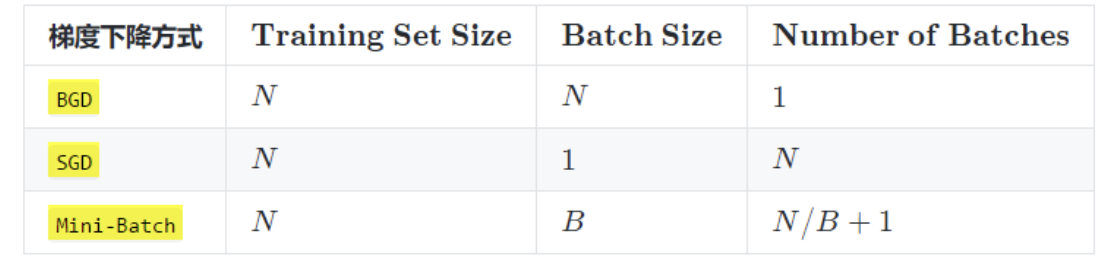
notes ： The above table Mini-Batch Of Batch The number is N / B + 1 It's for undivided cases . Divisible is N / B.

Suppose the data set has 50000 Training samples , Choose now Batch Size = 256 Train the model .

• Every Epoch Number of pictures to train ：50000
• The training set has Batch Number ：50000/256+1=196
• Every Epoch With Iteration Number ：196
• 10 individual Epoch With Iteration Number ：1960

2. Back propagation algorithm （BP Algorithm ）

The back propagation algorithm is used to train the neural network . This method is combined with gradient descent algorithm , Calculate the gradient of loss function for all weights in the network , The gradient value is used to update the weight to minimize the loss function . Introducing BP Before the algorithm , Let's first look at the content of forward propagation and chain rule .

2.1 Forward propagation and back propagation

Forward propagation refers to data input in a neural network , Layer by layer forward transmission , Until the operation reaches the output layer .

In the process of network training, there is always a certain error between the final result obtained after forward propagation and the real value of training samples , This error is the loss function . To reduce this error , Just use the loss function ERROR, From back to front , Find the partial derivative of each parameter in turn , This is back propagation （Back Propagation）.

2.2 The chain rule

The back propagation algorithm uses the chain rule to solve the gradient and update the weight . For complex compound functions , We split it into a series of addition, subtraction, multiplication and division or exponents , logarithm , Trigonometric functions and other elementary functions , Complete the derivation of composite function through chain rule . For the sake of simplicity , Here is an example of a common composite function in neural network to illustrate This process . Let the compound function 𝑓(𝑥; 𝑤, 𝑏) by :

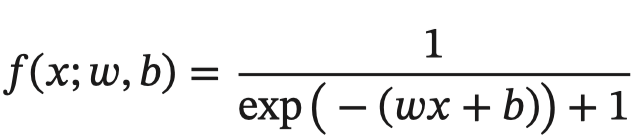
among x It's input data ,w Weight. ,b It's bias . We can decompose the composite function into ：

And graphical representation , As shown below ：

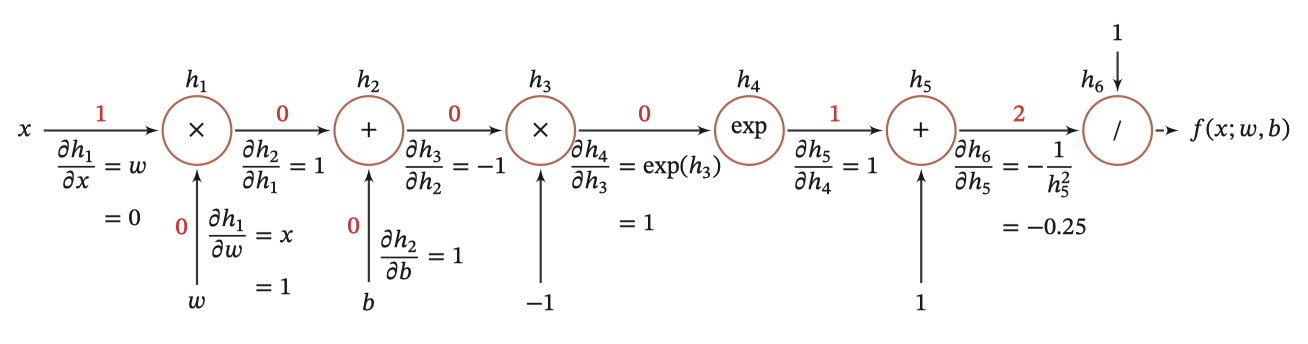
The whole composite function 𝑓(𝑥; 𝑤, 𝑏) About parameters 𝑤 and 𝑏 The derivative of can be obtained by 𝑓(𝑥; 𝑤, 𝑏) With the parameters 𝑤 and 𝑏 Multiply all the derivatives on the path between to get , namely ：

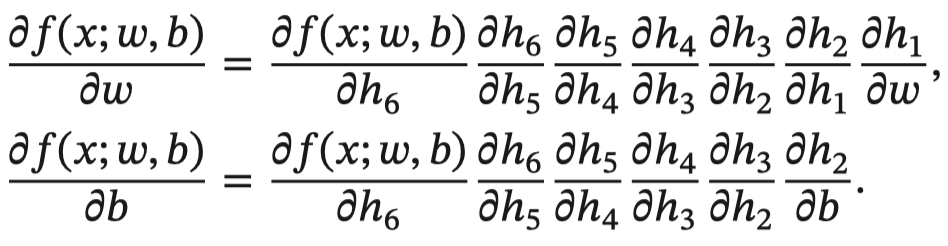
With w For example , When 𝑥 = 1, 𝑤 = 0, 𝑏 = 0 when , You can get ：

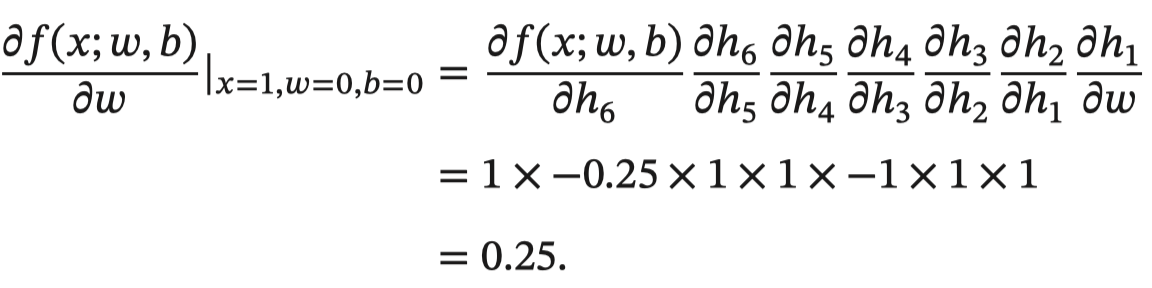
Be careful ： Derivatives of commonly used functions ：

2.3 Back propagation algorithm

The back-propagation algorithm updates the weight of each node in the neural network by using the chain rule . Let's introduce the whole process through an example ：

【 Take a chestnut ：】

As shown in the figure below, a simple neural network is used as an example ： The activation function is sigmoid

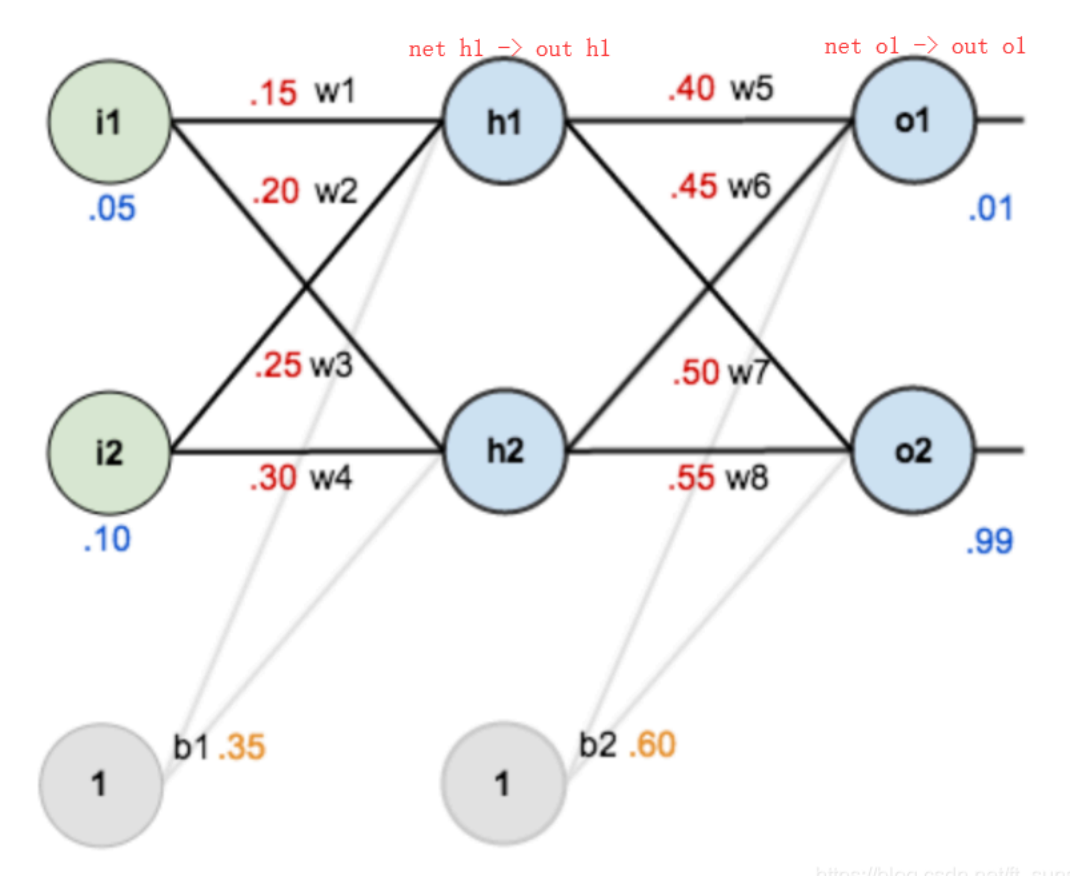
Forward propagation operation ：

Next is Back propagation （ Find the gradient of network error on each weight parameter ）：

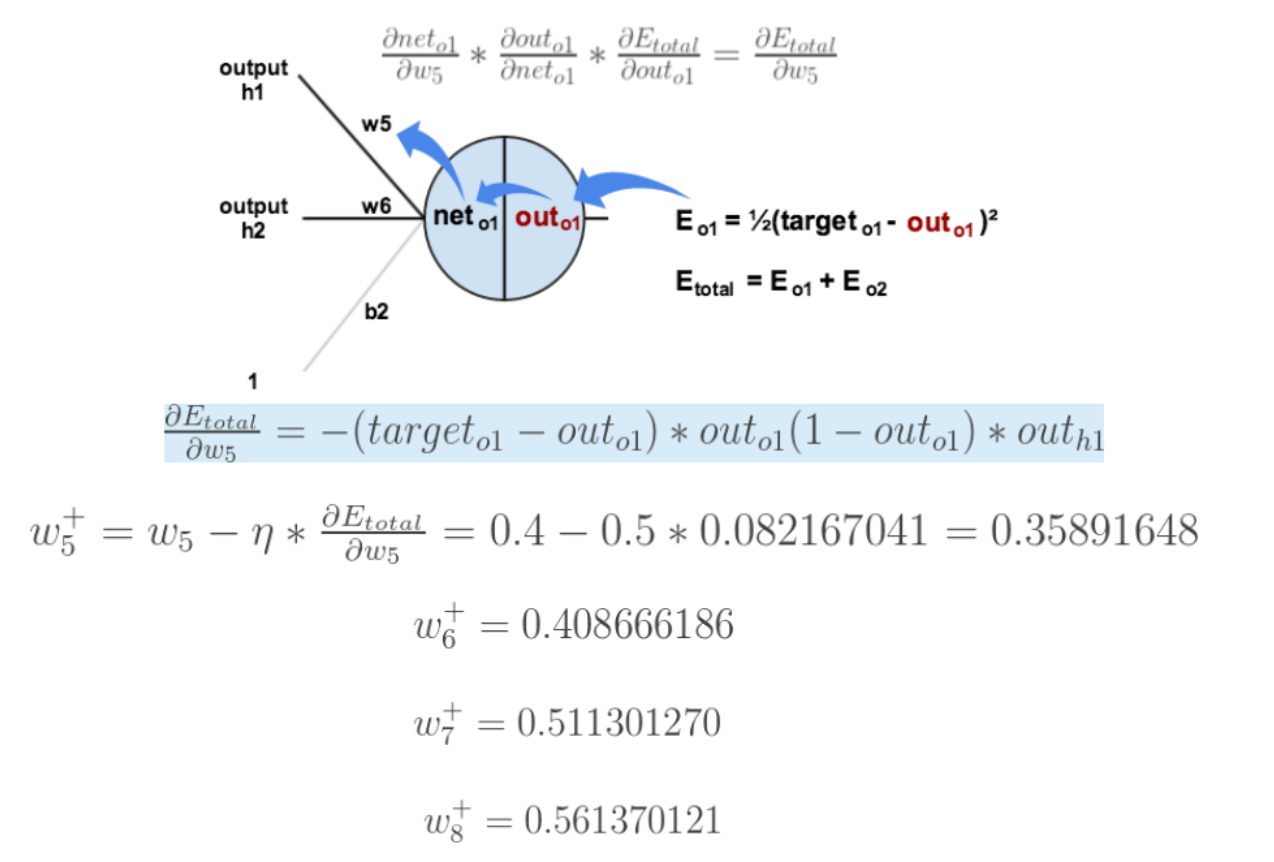
Let's start with the simplest , Find the error E Yes w5 The derivative of . First of all, make it clear that this is a “ The chain rule ” The derivation process of , Required error E Yes w5 The derivative of , You need to find the error first E Yes out o1 The derivative of , Ask again out o1 Yes net o1 The derivative of , Finally, ask net o1 Yes w5 The derivative of , After this The chain rule , We can find the error E Yes w5 The derivative of （ Partial Guide ）, As shown in the figure below ：

derivative （ gradient ） It has been calculated , The following is Back propagation and parameter updating process ：

If you want to ask error E Yes w1 The derivative of , error E Yes w1 There is more than one derivative path , It's a little more complicated , But change the soup without changing the medicine , The calculation process is shown as follows ：

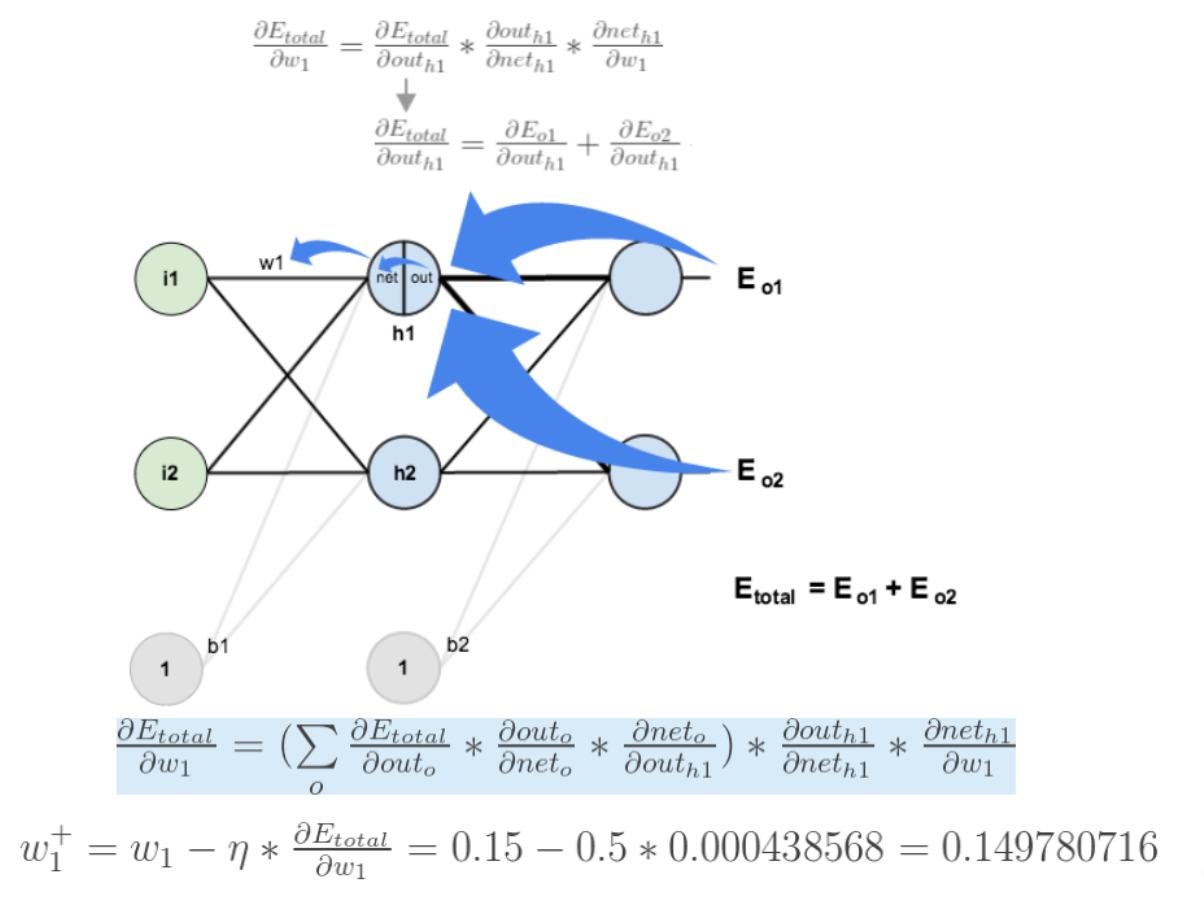
thus , Back propagation algorithm The process is over ！

3. Gradient descent optimization method

Gradient descent algorithm is used in network training , You'll meet a saddle point , Local minima these problems , How can we improve SGD Well ？ Here we introduce some commonly used

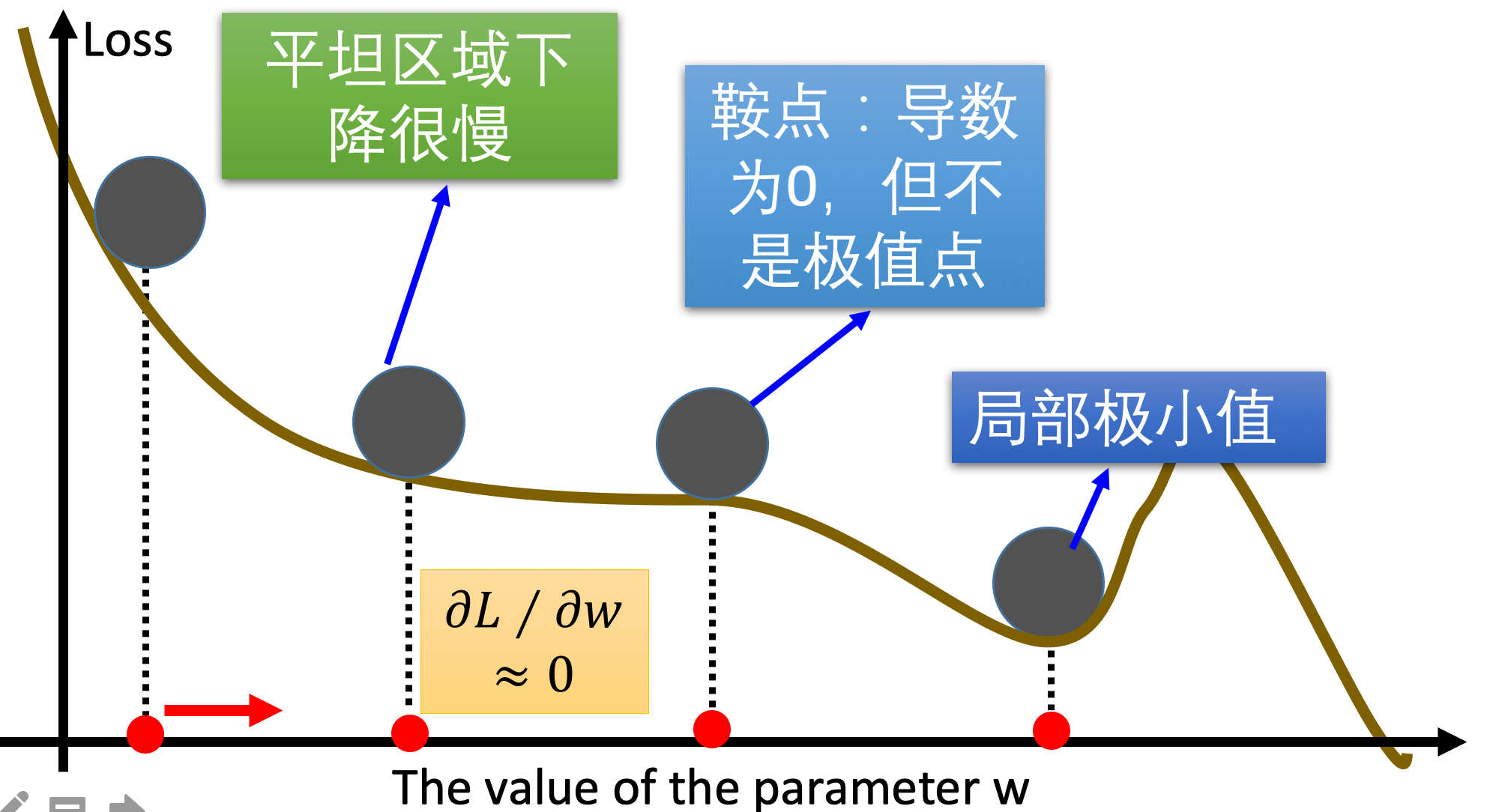
3.1 Momentum algorithm （Momentum）

The momentum algorithm mainly solves the saddle point problem . Before introducing the momentum method , Let's first look at the calculation method of exponential weighted average .

Exponentially weighted average
Suppose given a sequence , For example, the daily temperature in Beijing in a year , The blue dots in the figure represent real data ,

At this time, the temperature fluctuates greatly , Then we use the weighted average to smooth , As shown in the figure below, the red line is the result of smoothing ：

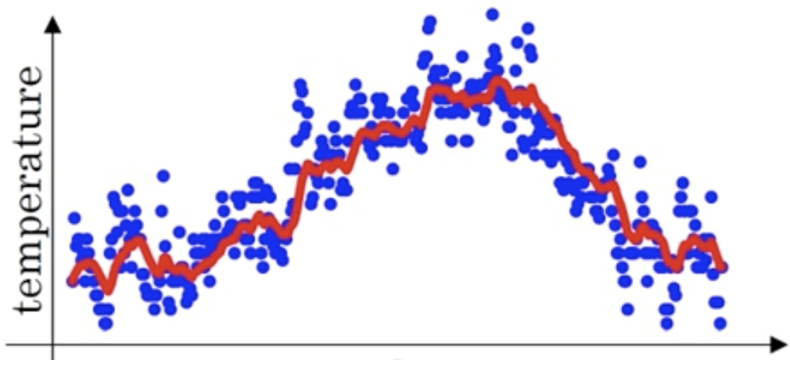
The calculation method is as follows ：

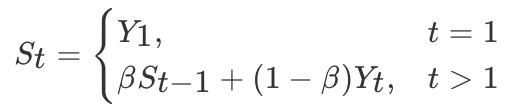
among Yt by t The real value at the moment ,St by t Weighted average value ,β Is the weight value . The red line is the result of exponential weighted average .

Above picture β Set to 0.9, Then the calculation result of exponential weighted average is ：

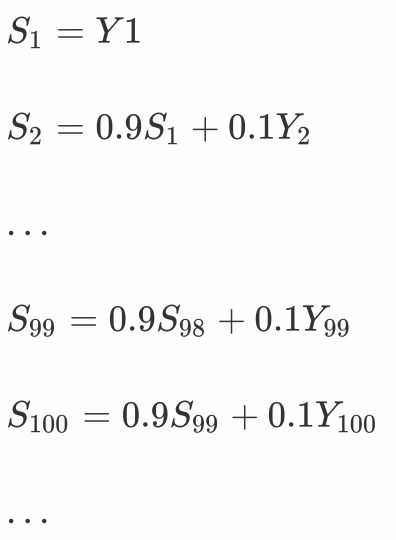
So the first 100 The result of days can be expressed as ：

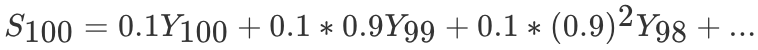
Momentum gradient descent algorithm
Momentum gradient descent （Gradient Descent with Momentum） Calculate the exponential weighted average of the gradient , And use this value to update the parameter value . The whole process of momentum gradient descent method is , among β Usually set to 0.9：

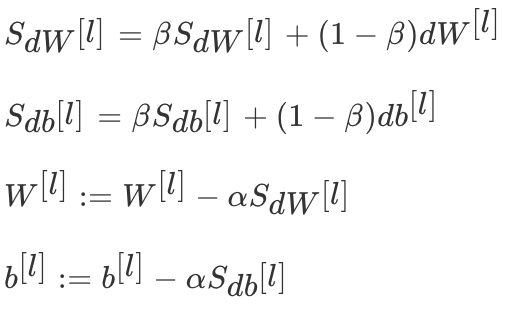
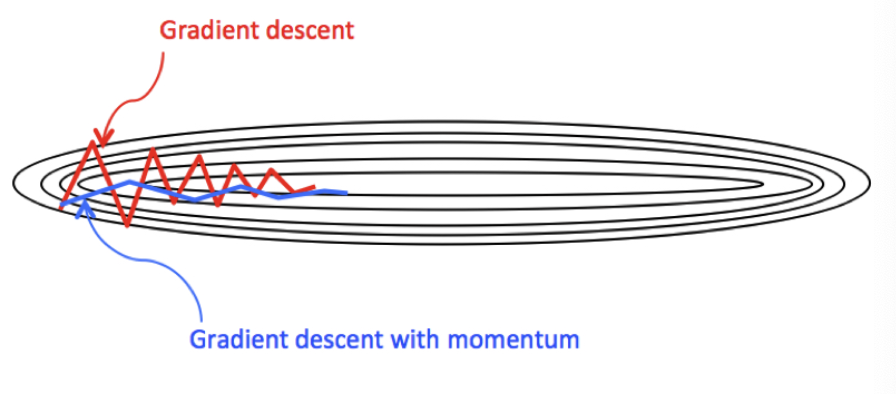
Compared with the original gradient descent algorithm , Its downward trend is smoother .

stay tf.keras Use in Momentum The algorithm still uses the function SGD Method , But set momentum Parameters , The implementation process is as follows ：

#  Import the corresponding toolkit 
import tensorflow as tf
#  Instantiate optimization methods ：SGD  Specify the parameters beta=0.9
opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9)
#  Define the parameters to be adjusted , Initial value 
var = tf.Variable(1.0)
val0 = var.value()
#  Define the loss function 
loss = lambda: (var ** 2)/2.0         
# First update ： Calculate the gradient , And update the parameters , In steps of  `- learning_rate * grad`
opt.minimize(loss, [var]).numpy()
val1 = var.value()
#  Second update ： Calculate the gradient , And update the parameters , Because of joining momentum, The step size will increase 
opt.minimize(loss, [var]).numpy()
val2 = var.value()
#  Print the step size of two updates 
print(" First update step ={}".format((val0 - val1).numpy()))
print(" The second update step ={}".format((val1 - val2).numpy()))

The result is ：

 First update step =0.10000002384185791
 The second update step =0.18000000715255737

There is also a momentum algorithm Nesterov accelerated gradient(NAG), According to the momentum term Pre estimate Parameters of , stay Momentum Further accelerate the convergence , Improve responsiveness , The algorithm implementation still uses SGD Method , To set up nesterov Set to true.

3.2 AdaGrad

AdaGrad The algorithm uses a small batch of random gradients $g_t$ By the sum of the squares of the elements st. At the first iteration ,AdaGrad take s0 Each element in is initialized to 0. stay t Sub iteration , First of all, a small batch of random gradients gt Add up the variable by the square of the element st：

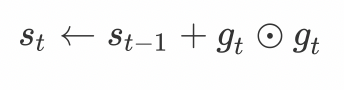
among ⊙ Multiply by elements . next , Let's readjust the learning rate of each element in the independent variable of the objective function by element operation ：

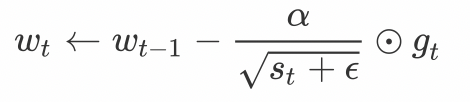
among α It's the learning rate ,ϵ Is a constant added to maintain numerical stability . It's Square here 、 Division and multiplication are based on elements . These operations by element make each element in the independent variable of the objective function have its own learning rate .

stay tf.keras The implementation method in is ：

tf.keras.optimizers.Adagrad(
    learning_rate=0.001, initial_accumulator_value=0.1, epsilon=1e-07
)

Example is ：

#  Import the corresponding toolkit 
import tensorflow as tf
#  Instantiate optimization methods ：SGD
opt = tf.keras.optimizers.Adagrad(
    learning_rate=0.1, initial_accumulator_value=0.1, epsilon=1e-07
)
#  Define the parameters to be adjusted 
var = tf.Variable(1.0)
#  Define the loss function ： No parameter but return value 
def loss(): return (var ** 2)/2.0

#  Calculate the gradient , And update the parameters ,
opt.minimize(loss, [var]).numpy()
#  Display the parameter update results 
var.numpy()

3.3 RMSprop

AdaGrad The learning rate of the algorithm is too small in the later stage of iteration , It is difficult to find the optimal solution . To solve this problem ,RMSProp Algorithm to AdaGrad The algorithm has made a little modification .

differ AdaGrad State variables in the algorithm st It's the deadline step t All small batch random gradients gt By the sum of the squares of the elements ,RMSProp（Root Mean Square Prop） The algorithm makes these gradients exponentially weighted moving average according to the square of the elements

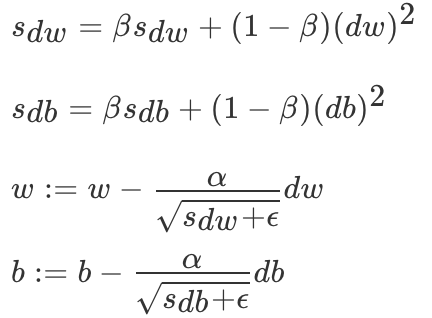
among ϵ It's the same. In order to maintain numerical stability, a constant . Finally, the learning rate of each element of the independent variable will not decrease all the time in the iterative process .RMSProp It helps to reduce the swing on the path to the minimum value , And allow for a greater learning rate α, So as to speed up the learning speed of the algorithm .

stay tf.keras When implemented in , The way to do it is ：

tf.keras.optimizers.RMSprop(
    learning_rate=0.001, rho=0.9, momentum=0.0, epsilon=1e-07, centered=False,
    name='RMSprop', **kwargs
)

Example ：

#  Import the corresponding toolkit 
import tensorflow as tf
#  Instantiate optimization methods RMSprop
opt = tf.keras.optimizers.RMSprop(learning_rate=0.1)
#  Define the parameters to be adjusted 
var = tf.Variable(1.0)
#  Define the loss function ： No parameter but return value 
def loss(): return (var ** 2)/2.0

#  Calculate the gradient , And update the parameters ,
opt.minimize(loss, [var]).numpy()
#  Display the parameter update results 
var.numpy()

The output is ：

0.6837723

3.4 Adam

Adam optimization algorithm （Adaptive Moment Estimation, Adaptive moment estimation ） take Momentum and RMSProp Algorithms are combined .Adam Algorithm in RMSProp On the basis of the algorithm, we also do exponential weighted moving average for small batch of random gradients .

Suppose you use each mini-batch Calculation dW、db, The first t Times of iteration ：

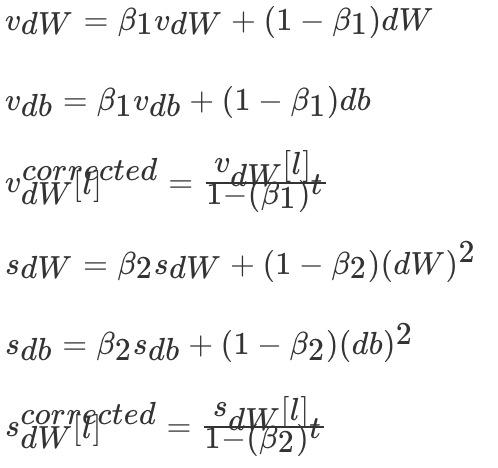
among l For a certain layer ,t Is the value of the moving average

Adam Parameter update of the algorithm ：

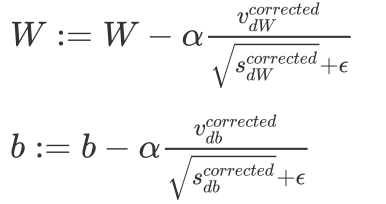
Recommended parameter setting values ：

• Learning rate α： You need to try a series of values , To find a more suitable
• β1： The common default value is 0.9
• β2： The suggestion is 0.999
• ϵ： The default value is 1e-8

stay tf.keras The method implemented in is ：

tf.keras.optimizers.Adam(
    learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07
)

Example ：

#  Import the corresponding toolkit 
import tensorflow as tf
#  Instantiate optimization methods Adam
opt = tf.keras.optimizers.Adam(learning_rate=0.1)
#  Define the parameters to be adjusted 
var = tf.Variable(1.0)
#  Define the loss function ： No parameter but return value 
def loss(): return (var ** 2)/2.0

#  Calculate the gradient , And update the parameters ,
opt.minimize(loss, [var]).numpy()
#  Display the parameter update results 
var.numpy()

The result is ：

0.90000033

4. Learning rate

When you train the neural network , Generally, the learning rate will change with training , This is mainly due to , In the later stage of neural network training , If the learning rate is too high , Can cause loss Oscillation of , But if the learning rate decreases too fast , It will cause the convergence to slow down .

4.1 Piecewise constant decay

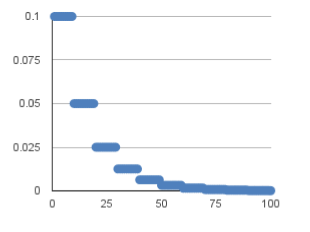
The piecewise constant attenuation is in the range of training times defined in advance , Set different learning rate constants . At the beginning, the learning rate is higher , Then it gets smaller and smaller , The interval setting needs to be adjusted according to the sample size , Generally, the larger the sample size is, the smaller the interval should be .

stay tf.keras The corresponding method in is ：

tf.keras.optimizers.schedules.PiecewiseConstantDecay(boundaries, values)

Parameters ：

• Boundaries: Set the of segmented updates step value
• Values: For the learning rate value without segmentation

Example ： For the former 100000 Step , The learning rate is 1.0, For the next 100000-110000 Step , The learning rate is 0.5, The learning rate of the following steps is 0.1

#  Set the number of segments step value 
boundaries = [100000, 110000]
#  Different step Corresponding learning rate 
values = [1.0, 0.5, 0.1]
#  Instantiation for learning updates 
learning_rate_fn = keras.optimizers.schedules.PiecewiseConstantDecay(
    boundaries, values)

4.2 Exponential decay

The exponential decay can be expressed by the following mathematical formula ,

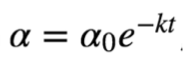
among ,t Represents the number of iterations ,α0,k It's a super parameter.

stay tf.keras The implementation of ：

tf.keras.optimizers.schedules.ExponentialDecay(initial_learning_rate, decay_steps,decay_rate)

The concrete realization is ：

def decayed_learning_rate(step):
      return initial_learning_rate * decay_rate ^ (step / decay_steps)

Parameters ：

Initial_learning_rate: Initial learning rate ,α0

decay_steps: k value

decay_rate: The bottom of the index

4.3 1/t attenuation

1/t The attenuation can be expressed by the following mathematical formula ：

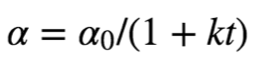
among ,t Represents the number of iterations ,α0,k It's a super parameter.

stay tf.keras The implementation of ：

tf.keras.optimizers.schedules.InverseTimeDecay(initial_learning_rate, decay_steps,
                                               decay_rate)

The concrete realization is ：

def decayed_learning_rate(step):
  return initial_learning_rate / (1 + decay_rate * step / decay_step)

Parameters ：

Initial_learning_rate: Initial learning rate ,α0

decay_step/decay_steps: k value

summary

• Know the gradient descent algorithm
  A way to find a way to minimize the loss function ： Batch gradient descent , Stochastic gradient descent , Small batch gradient descent

• Understand the chain rule of neural network
  Derivation of compound function

• Master the back propagation algorithm （BP Algorithm ）
  Method of updating parameters by neural network

• Know the optimization method of gradient descent algorithm
  Momentum algorithm ,adaGrad,RMSProp,Adam

• Understanding learning rate annealing
  Piecewise constant decay , Exponential decay ,1/t attenuation