当前位置:网站首页>知否|两大风控最重要指标与客群好坏的关系分析
知否|两大风控最重要指标与客群好坏的关系分析
2022-07-07 12:58:00 【番茄风控】
在风控建模中,变量WOE是一个经常提到的概念,无论在实际业务的工作场景,还是在风控岗位的面试环节,我们往往会与WOE不期而遇。那么,变量WOE为什么如此重要,或者说在实际建模过程中有哪些突出贡献,是我们从事风控数据分析工作必须要掌握的知识点之一。本文将会围绕变量WOE的原理逻辑与应用场景,来具体介绍下WOE在数据分析中展现出的重要特点。
1、WOE原理逻辑
WOE(weight of evidence):证据权重,表示特征变量离散后在分箱区间好坏样本的分布差异,WOE的绝对值越大,说明好坏分布的差异越明显。特征变量WOE的计算公式有两种表达方式,具体如下图1所示,其中Goodi、Badi分别代表变量分箱区间i的好、坏样本数量,GoodT、BadT分别代表特征数据的好、坏总样本数量,WOEi为当前分箱区间的证据权重值。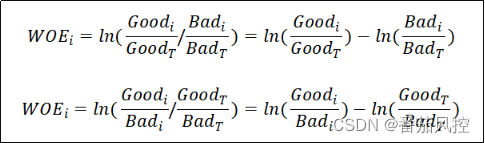
图1 WOE原理公式
针对以上WOE公式,可以从两个角度来进行描述,第一个公式可理解为每个分箱好样本分布与坏样本分布之间的差异,第二个公式可理解为每个分箱好坏样本比与总体好坏样本比之间的差异。无论从哪个推导公式理解,其核心思想都是一致的,即描述变量分箱区间好坏样本分布的差异性,且最终变量WOE结果都是相同的。现通过实际样例进行验证说明,假设某特征变量离散分为10个分箱(bin),统计每个分 箱的好、坏样本数量分别为G_cnt、B_cnt,样本所有好、坏样本数量分别为G_tot、B_tot,通过以上WOE两种计算公式得到的变量各分箱WOE结果,具体如图2、图3所示
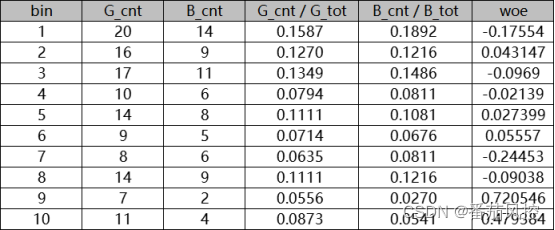
图2 WOE原理逻辑1
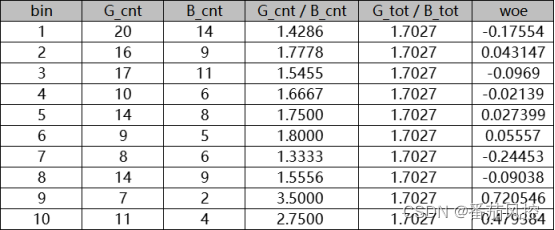
图3 WOE原理逻辑2
由上图分布结果可知,两种描述方式下的各分箱WOE结果值是一致的,只是表现形式的区别。同时,从最终结果可以看出,随着变量各分箱区间好坏样本的差异变化,WOE可以取正值、负值或0各种情况。这里需要注意的是,WOE取值的正负与大小,正是我们需要重点关注的内容,而且连续分箱区间的WOE变化关系,能够较大程度体现变量的区分能力与业务属性。
以图2的变量WOE分布结果为例,分箱bin=1对应的WOE结果为-0.17554,表明此分箱区间中坏样本的表现程度较大,且WOE为负数时的绝对值越大,样本分布坏的程度越大;与之相反的是,分箱bin=2对应的WOE结果为0.043147,表明此分箱区间中好样本的表现程度越大,且WOE为正数时的绝对值越大,样本分布好的程度越大;当分箱区间的WOE为0时,说明好坏样本的表现程度相当。
此外,需要说明的是,WOE取值的正负分别代表样本好坏的程度,这个规律并不是绝对的,具体意义取决于WOE的计算公式设置。当样本分布的比较关系为好比坏(Good/Bad)时,那么WOE为正时代表样本好的程度较高;当样本分布的比较关系为坏比好(Bad/Good)时,那么WOE为正时代表样本坏的程度较高。
2、WOE好坏分析
为了进一步来分析变量分箱区间WOE的业务含义,我们针对图2变量WOE的分布结果,进一步加工出各分箱区间的其他分析指标:坏账率badrate与信息值IV,其计算逻辑公式如图4所示。
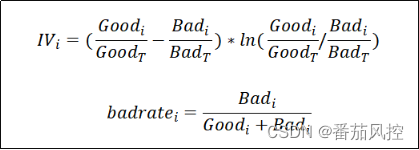
图4 IV与badrate逻辑
由以上公式可知,信息值IV可以进一步推导为(Goodi/GoodT-Badi/BadT)*WOEi,表示各区间好坏样本占比差值与WOE的乘积关系。此外,根据变量IV的计算公式很容易证明,IV值不可能为负数。变量的IV值大小为所有分箱区间IV值之和,当IV=0时说明变量无区分度,而随着IV取值的增大,变量区分好坏样本的能力越强,这个原理在特征变量筛选的场景中经常使用到,而且在建立例如逻辑回归等模型过程中的重要步骤。变量区间的指标坏账率badrate则直接体现了分箱区间样本的好坏程度,即坏样本占当前区间好坏总样本的比例,通过与整体样本坏账率的对比分析,可以清晰的比较出分箱区间的样本好坏程度。图2样本分布对应的IV与badrate指标结果,具体如图5所示。
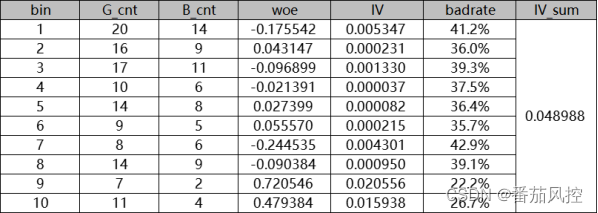
图5 IV与badrate结果
从上图结果可知,整个样本的坏账率为sum(G_cnt)/sum(G_cnt,B_cnt)=37%,变量分箱区间的WOE为负值时,说明区间样本坏的程度相对较高(相对整体样本平均好坏程度),例如图中分箱bin=1、3、4、7、8区间的WOE均为负数,对应坏账率badrate均高于全量样本的坏账率(37%);而变量分箱区间的WOE为正值时,说明区间样本好的程度相对较高,例如图中分箱bin=2、5、6、9、10区间的WOE均为正数,对应坏账率badrate均低于全量样本的坏账率(37%)。
同时,无论变量区间WOE值为正或负,其绝对值越大,说明样本群体好或坏的程度越高,例如分箱bin=1与bin=3进行对比,WOE分别为-0.175542、-0.096899,前者相比后者的绝对值较大,说明样本坏的程度更高,对应到坏账率badrate分别为41.2%、39.3%直接验证了这个规律。再例如bin=9与bin=10进行对比,WOE分别为0.020556、0.015938,首先是正值说明这两个区间样本相比整体样本分布是偏好的,然后是前者的绝对值大于后者,说明样本好的程度更高,再来看对应的坏账率badrate分别为22.2%、26.7% ,前者优于后者同样验证了样本群体好坏程度的分析逻辑。
这便是通过WOE指标来分析变量区间样本群体好坏程度的思路,这在评估变量区分能力方面具有很好的效果,相比badrate指标分析来讲,WOE不仅可以通过取值的正负关系体现出区间样本相比整体样本的好坏偏向,而且能够根据取值的大小关系来进一步量化样本群体的好坏程度。同时,当WOE=0时直接说明区间的好坏程度与整体样本的平均分布一致,并不需要提前预知全量样本坏账率的具体大小,从这些角度可以综合说明,采用变量WOE值来评价分箱样本群体的分布特点有着很好的作用。此外,对于连续变量的WOE值分布,可以进一步用来分析变量区分度的单调性,为建模特征变量的筛选提供比较方便的参考依据。图5变量的WOE分布趋势通过可视化展示如图6所示,由最终趋势结果可见,此变量的区分度没有明显的单调性,对于建立逻辑回归等解释性较强的模型来讲,不便于将其采纳进入模型拟合变量池
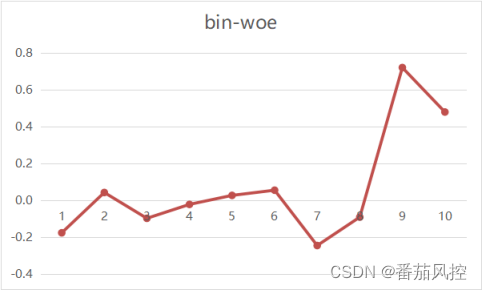
图6 变量WOE分布趋势
3、IV区分能力
在图5的指标结果中,我们同步得到了变量各分箱区间的IV值大小,可以了解到,WOE的绝对值越大,IV值越大,从业务角度来描述,那就是区间好坏样本的差异性越大,好坏样本的区分能力越好。对于变量最终的IV值,是由所有区间的IV值求和得到,结果取值越大,说明变量的区分能力(预测能力)越强。针对图5样例的变量IV值为0.048988,在实际业务场景中如何来评价,或者是否可以作为建模变量选择,并没有绝对的标准,具体需要根据样本情况与业务需求综合决定。但是,一般情况下,变量IV值大小代表的区分能力强弱,在业务中已形成了一个较为通用的参考标准,具体如图7所示,实践过程中可以综合应用。
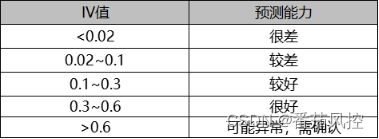
图7 变量IV评估标准
4、WOE与IV实例
通过以上内容介绍,我们整体熟悉了变量WOE的计算逻辑与分析方法,以及WOE与IV之间的关系,尤其是采用WOE来分析变量分箱样本群体的好坏程度,并评估变量区分能力的单调性趋势,是我们日常数据分析工作必须要掌握的要点。下面我们结合一份具体样本数据,通过代码来实现变量WOE与IV的指标输出。样本数据(前10)如图8所示,包含6000条样本与6个字段,其中ID为样本主键,X1~X4为特征变量,Y为目标变量(取值0/1分别代表好坏)。
图8 样本数据
现采用等频分箱方式将特征变量X1~X4离散为10箱,并将各区间的好坏数量、好坏占比、坏账率、WOE、IV等指标统一输出,具体实现代码如图9所示。
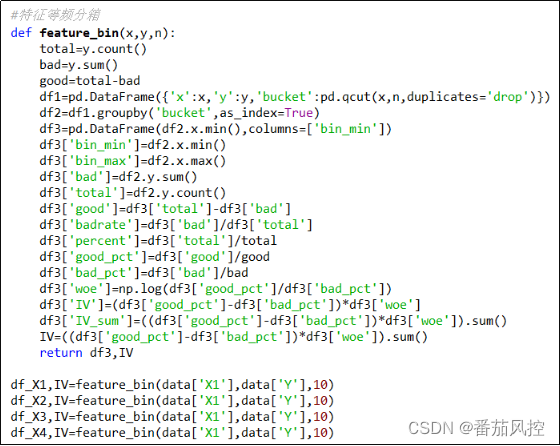
图9 特征分箱实现
以特征X1为例,最终分箱结果如图10所示,从表中信息可知,由于采用等频分箱方式,各个区间的样本占比(percent)均在10%附近。根据变量woe分布可以看出,变量X1随着分箱区间数值的增加,好坏样本之间的差异性逐渐向好的方向发展,指标坏账率badrate也能验证这个趋势,且woe呈现的单调性也较好,如图11所示。
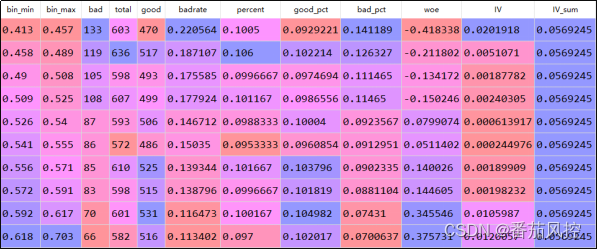
图10 变量X1分箱结果
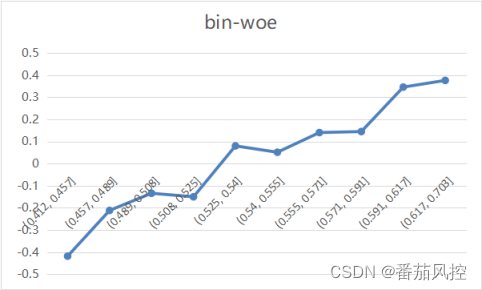
图11 变量X1单调性
为了快速将样本数据所有特征变量的IV值进行输出,可以采用图12所示的循环代码实现,样本数据的变量X1~X4最终IV结果如图13所示。当然,如果调整分箱数量大小,或者采用其他分箱方式(等距分箱、卡方分箱等),变量分箱区间的WOE值以及变量整体的IV值都会有所变化的,具体需要结合实际业务场景的情况而定,但无论采取哪种分箱方式,对于特征分箱后的WOE与IV的分析逻辑及其应用思路是一致的。

图12 特征批量分箱

图13 样本特征IV值
以上内容便是围绕特征WOE的原理逻辑与研究思路,介绍了WOE指标在实际场景中分析样本好坏差异的应用,并结合变量IV值描述了二者在特征离散分箱后的特征评估价值。为了便于大家对本文知识要点的进一步理解与掌握,本文额外附带了与以上实例分析内容同步的样本数据与python代码,供大家参考学习,详情请移至知识星球查看相关内容。
…
~原创文章
边栏推荐
猜你喜欢
Niuke real problem programming - day16
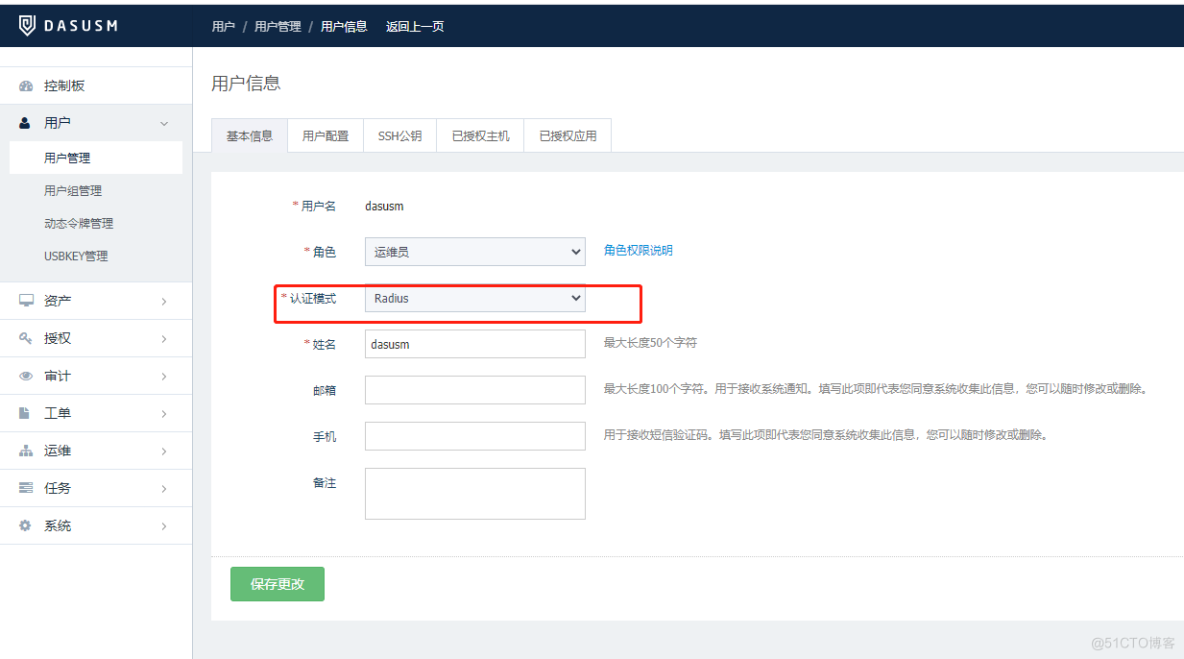
How to enable radius two factor / two factor (2fa) identity authentication for Anheng fortress machine
Cocoscreator operates spine for animation fusion
![[机缘参悟-40]:方向、规则、选择、努力、公平、认知、能力、行动,读3GPP 6G白皮书的五层感悟](/img/38/cc5bb5eaa3dcee5ae2d51a904cf26a.png)
[机缘参悟-40]:方向、规则、选择、努力、公平、认知、能力、行动,读3GPP 6G白皮书的五层感悟

众昂矿业:萤石继续引领新能源市场增长

数学建模——什么是数学建模

Ctfshow, information collection: web12
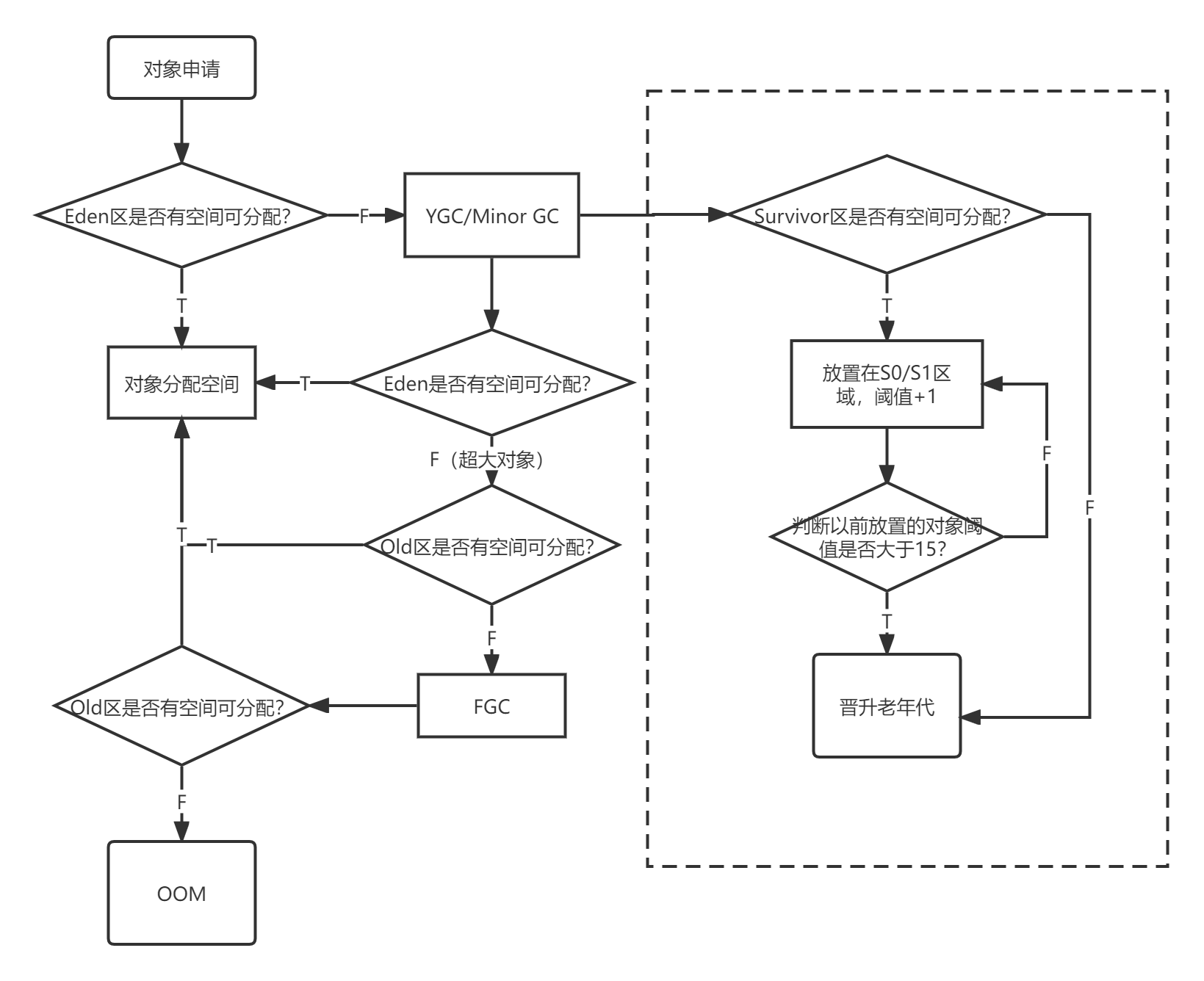
⼀个对象从加载到JVM,再到被GC清除,都经历了什么过程?

大厂做开源的五大痛点
13 ux/ui/ue best creative inspiration websites in 2022
随机推荐
Simple steps for modifying IP of sigang electronic scale
Stream learning notes
在软件工程领域,搞科研的这十年!
Used by Jetson AgX Orin canfd
Classification of regression tests
PAT 甲级 1103 Integer Factorizatio
Niuke real problem programming - day16
Ctfshow, information collection: web2
Niuke real problem programming - day13
【OBS】RTMPSockBuf_Fill, remote host closed connection.
智汀不用Home Assistant让小米智能家居接入HomeKit
Today's sleep quality record 78 points
word中删除一整页
Apache多个组件漏洞公开(CVE-2022-32533/CVE-2022-33980/CVE-2021-37839)
@ComponentScan
CTFshow,信息搜集:web2
Niuke real problem programming - Day10
《微信小程序-进阶篇》组件封装-Icon组件的实现(一)
Introduction and use of Kitti dataset
leetcode 241. Different Ways to Add Parentheses 为运算表达式设计优先级(中等)