当前位置:网站首页>[combinatorics] permutation and combination (multiple set permutation | multiple set full permutation | multiple set incomplete permutation all elements have a repetition greater than the permutation
[combinatorics] permutation and combination (multiple set permutation | multiple set full permutation | multiple set incomplete permutation all elements have a repetition greater than the permutation
2022-07-03 12:50:00 【Programmer community】
List of articles
- One 、 Multiple sets
- Two 、 Full Permutation of multiple sets
- 3、 ... and 、 Examples of Full Permutation of multiple sets
- 3、 ... and 、 Multiset incomplete permutation 1 The repetition of all elements is greater than the number of permutations (
n
i
≥
r
n_i \geq r
ni≥r )
- Four 、 Multiset incomplete permutation 2 The repetition of some elements is less than the number of permutations (
n
i
≤
r
n_i \leq r
ni≤r )
Arrange and combine reference blogs :
- 【 Combinatorial mathematics 】 Basic counting principle ( The principle of addition | Multiplication principle )
- 【 Combinatorial mathematics 】 Examples of permutation and combination of sets ( array | Combine | Circular arrangement | binomial theorem )
- 【 Combinatorial mathematics 】 Permutation and combination ( Arrange and combine content summary | Select the question | Set arrangement | Set combination )
- 【 Combinatorial mathematics 】 Permutation and combination ( Examples of permutations )
One 、 Multiple sets
Multiset representation :
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
,
0
≤
n
i
≤
+
∞
S = \{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \} , \ \ \ 0 \leq n_i \leq +\infty
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}, 0≤ni≤+∞
- Type of elements : Multiple sets contain
k
k
k Different elements ,
- The element represents : Each element is represented as
a
1
,
a
2
,
⋯
,
a
k
a_1 , a_2 , \cdots , a_k
a1,a2,⋯,ak ,
- Element number : The number of occurrences of each element is
n
1
,
n
2
,
⋯
,
n
k
n_1, n_2, \cdots , n_k
n1,n2,⋯,nk ,
- The value of the number of elements :
n
i
n_i
ni The value requirement of is Greater than
0
0
0 , Less than positive infinity
+
∞
+ \infty
+∞ ;
Two 、 Full Permutation of multiple sets
Multiple sets :
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
,
0
≤
n
i
≤
+
∞
S = \{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \} , \ \ \ 0 \leq n_i \leq +\infty
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}, 0≤ni≤+∞
* Full Permutation :
r
=
n
1
+
n
2
+
⋯
+
n
k
=
n
r = n_1 + n_2 + \cdots + n_k = n
r=n1+n2+⋯+nk=n
N
=
n
!
n
1
!
n
2
!
⋯
n
k
!
N = \cfrac{n!}{n_1! n_2! \cdots n_k!}
N=n1!n2!⋯nk!n!
* The total permutation number of a multiset is Factorial of the total number of elements , Divide Factorial of all repetitions ;
Here's the derivation process
Yes
k
k
k Elements ,
Place the elements
a
1
a_1
a1 : Put the first element in the arrangement
a
1
a_1
a1 , This element has
n
1
n_1
n1 individual ,
n
n
n Select from two positions
n
1
n_1
n1 individual Location , Yes
C
(
n
,
n
1
)
C(n, n_1)
C(n,n1) Methods ;
C
(
n
,
n
1
)
=
n
!
(
n
−
n
1
)
!
n
1
!
C(n, n_1) = \cfrac{n!}{(n-n_1) ! \ n_1!}
C(n,n1)=(n−n1)! n1!n!
Place the elements
a
2
a_2
a2 : Put it in place
n
1
n_1
n1 Then put the second element
a
2
a_2
a2 , This element has
n
2
n_2
n2 individual , And then there is
n
−
n
1
n-n_1
n−n1 Empty space , from
n
−
1
n-1
n−1 Choose among the positions
n
2
n_2
n2 There are two positions
C
(
n
−
n
1
,
n
2
)
C(n-n_1 , n_2)
C(n−n1,n2) Methods ;
C
(
n
−
n
1
,
n
2
)
=
(
n
−
n
1
)
!
(
n
−
n
1
−
n
2
)
!
n
2
!
C(n - n_1, n_2) = \cfrac{(n-n_1)!}{(n-n_1 - n_2) ! \ n_2!}
C(n−n1,n2)=(n−n1−n2)! n2!(n−n1)!
⋮
\vdots
⋮
Place the elements
a
k
a_k
ak : Place the last element
a
k
a_k
ak , This element has
n
k
n_k
nk individual , And then there is
n
−
n
1
−
⋯
−
n
k
−
1
n-n_1- \cdots -n_{k-1}
n−n1−⋯−nk−1 Empty space , from
n
−
n
1
−
⋯
−
n
k
−
1
n-n_1- \cdots -n_{k-1}
n−n1−⋯−nk−1 Choose among the positions
n
k
n_k
nk There are two positions
C
(
n
−
n
1
−
⋯
−
n
k
−
1
,
n
k
)
C(n-n_1- \cdots -n_{k-1} , n_k)
C(n−n1−⋯−nk−1,nk) Methods ;
C
(
n
−
n
1
−
⋯
−
n
k
−
1
,
n
k
)
=
(
n
−
n
1
−
⋯
−
n
k
−
1
)
!
(
n
−
n
1
−
⋯
−
n
k
−
1
−
n
k
)
!
n
k
!
C(n-n_1- \cdots -n_{k-1} , n_k) = \cfrac{(n-n_1- \cdots -n_{k-1})!}{(n-n_1- \cdots -n_{k-1} - n_k) ! \ n_k!}
C(n−n1−⋯−nk−1,nk)=(n−n1−⋯−nk−1−nk)! nk!(n−n1−⋯−nk−1)!
product rule : Finally, according to the law of multiplication , Multiply each of the above placement methods , You get the final result , Factorials look complicated , however Factorial options such as
(
n
−
n
1
−
⋯
−
n
k
−
1
)
!
(n-n_1- \cdots -n_{k-1})!
(n−n1−⋯−nk−1)! You can make an appointment , The final results are as follows :
N
=
C
(
n
,
n
1
)
C
(
n
−
n
1
,
n
2
)
C
(
n
−
n
1
−
⋯
−
n
k
−
1
,
n
k
)
=
n
!
(
n
−
n
1
)
!
n
1
!
×
(
n
−
n
1
)
!
(
n
−
n
1
−
n
2
)
!
n
2
!
×
(
n
−
n
1
−
⋯
−
n
k
−
1
)
!
(
n
−
n
1
−
⋯
−
n
k
−
1
−
n
k
)
!
n
k
!
about
fall
Ministry
branch
rank
ride
=
n
!
n
1
!
n
2
!
⋯
n
k
!
\begin{array}{lcl} N & = & C(n, n_1) C(n - n_1, n_2) C(n-n_1- \cdots -n_{k-1} , n_k) \\\\ & = & \cfrac{n!}{(n-n_1) ! \ n_1!} \times \cfrac{(n-n_1)!} {(n-n_1 - n_2) ! \ n_2!} \times \cfrac{(n-n_1- \cdots -n_{k-1})!}{(n-n_1- \cdots -n_{k-1} - n_k) ! \ n_k!} \ \ \ Omit some factorials \\\\ &=& \cfrac{n!}{n_1! n_2! \cdots n_k!} \end{array}
N===C(n,n1)C(n−n1,n2)C(n−n1−⋯−nk−1,nk)(n−n1)! n1!n!×(n−n1−n2)! n2!(n−n1)!×(n−n1−⋯−nk−1−nk)! nk!(n−n1−⋯−nk−1)! about fall Ministry branch rank ride n1!n2!⋯nk!n!
3、 ... and 、 Examples of Full Permutation of multiple sets
Finding multiple sets
S
=
{
3
⋅
a
,
2
⋅
b
,
1
⋅
c
}
S=\{ 3 \cdot a , 2 \cdot b , 1 \cdot c \}
S={ 3⋅a,2⋅b,1⋅c} The whole arrangement ?
The total number of elements in the above multiset is
n
=
3
+
2
+
1
=
6
n = 3 + 2 + 1 = 6
n=3+2+1=6 ;
The total number of permutations is :
N
=
6
!
3
!
×
2
!
×
1
!
=
6
×
5
×
4
×
3
×
2
×
1
(
3
×
2
×
1
)
×
(
2
×
1
)
×
(
1
×
1
)
=
60
N = \cfrac{6!}{3! \times 2! \times 1!} = \cfrac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{( 3 \times 2 \times 1 ) \times ( 2 \times 1 ) \times (1 \times 1)} = 60
N=3!×2!×1!6!=(3×2×1)×(2×1)×(1×1)6×5×4×3×2×1=60
3、 ... and 、 Multiset incomplete permutation 1 The repetition of all elements is greater than the number of permutations ( n
i
≥
r
n_i \geq r
ni≥r )
Multiple sets :
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
,
0
≤
n
i
≤
+
∞
S = \{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \} , \ \ \ 0 \leq n_i \leq +\infty
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}, 0≤ni≤+∞
* Incomplete permutation
1
1
1 :
r
≤
n
i
r \leq n_i
r≤ni , Notice the
r
r
r want Less than or equal to The smallest
n
i
n_i
ni ;
N
=
k
r
N = k^r
N=kr
Derivation process :
Under the above conditions ,
r
r
r A place ,
There are elements in every position
k
k
k A choice ,
According to the law of multiplication , The total number of choices is
k
×
k
×
⋯
×
k
⏟
r
individual
k
\begin{matrix} \underbrace{ k \times k \times \cdots \times k } \\ r individual k \end{matrix}
k×k×⋯×kr individual k ,
namely
r
k
r^k
rk ;
Four 、 Multiset incomplete permutation 2 The repetition of some elements is less than the number of permutations ( n
i
≤
r
n_i \leq r
ni≤r )
The above situation only applies to the situation where the repeatability is large enough , namely The repetition of each element is greater than the number of selections ,
r
≤
n
i
r \leq n_i
r≤ni
If The repetition of one element is less than the number of selections ,
r
≥
n
i
r \geq n_i
r≥ni ,
Such as
S
=
{
3
⋅
a
,
2
⋅
b
,
1
⋅
c
}
S=\{ 3 \cdot a , 2 \cdot b , 1 \cdot c \}
S={ 3⋅a,2⋅b,1⋅c} Three permutations of multiple sets , You can't use formulas ,
There is no formula for , But it can. Use The inclusion exclusion principle , Generating function Calculate ;
边栏推荐
- 写一个简单的nodejs脚本
- 【数据挖掘复习题】
- 2021 autumn Information Security Experiment 1 (password and hiding technology)
- 十条职场规则
- 启用MemCached的SASL认证
- Use bloc to build a page instance of shutter
- Gan totem column bridgeless boost PFC (single phase) seven PFC duty cycle feedforward
- GaN图腾柱无桥 Boost PFC(单相)七-PFC占空比前馈
- It feels great to know you learned something, isn‘t it?
- Export the entire Oracle Database
猜你喜欢
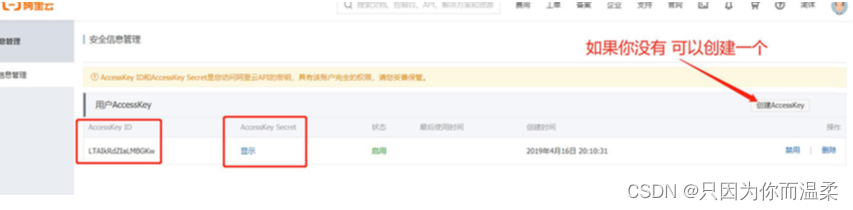
Alibaba is bigger than sending SMS (user microservice - message microservice)

Sword finger offer10- I. Fibonacci sequence

Summary of error prone knowledge points: Calculation of define s (x) 3*x*x+1.
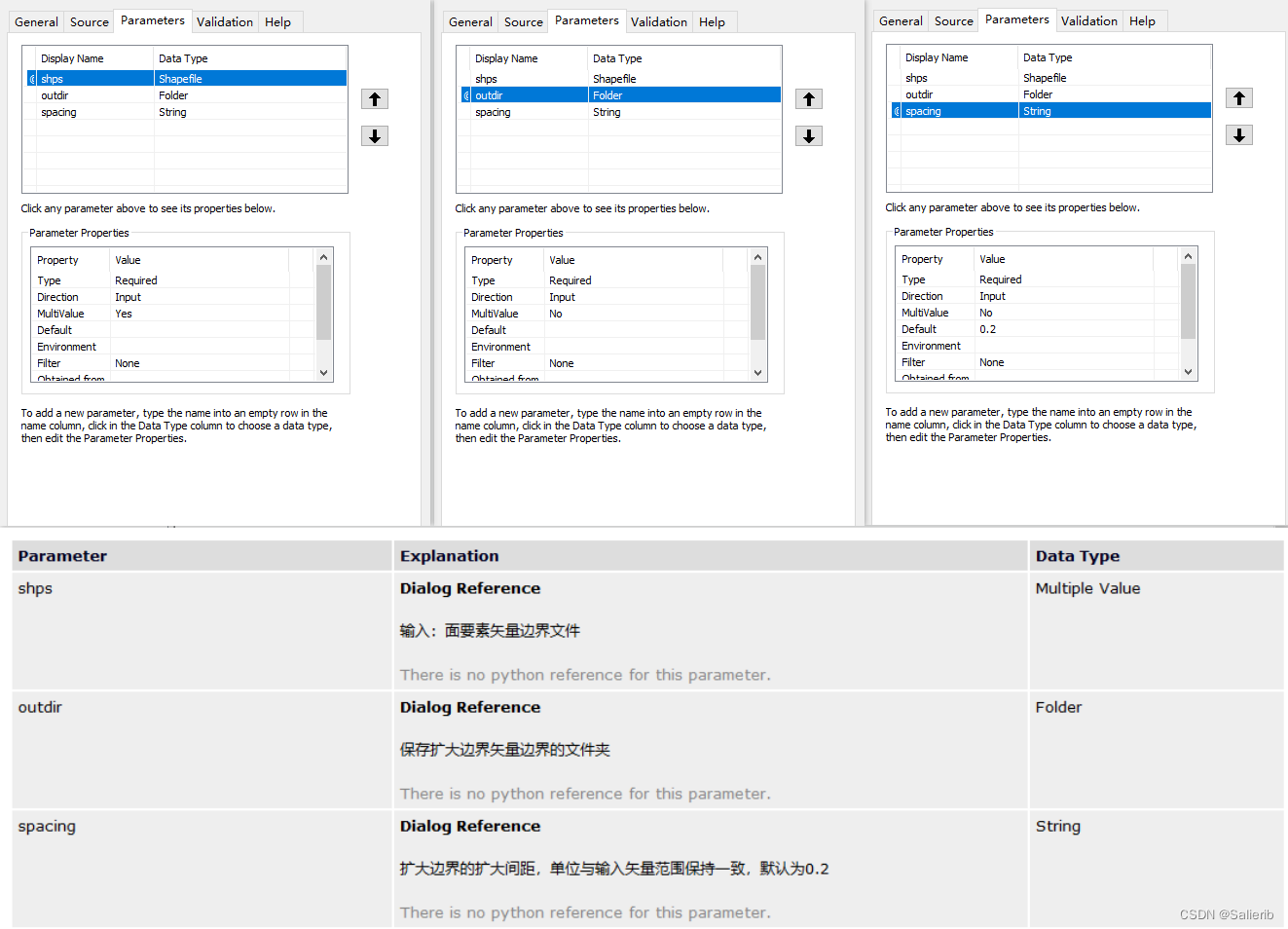
【ArcGIS自定义脚本工具】矢量文件生成扩大矩形面要素
![[review questions of database principles]](/img/c3/81d192a40bcc4f5d72fcbe76c708bb.png)
[review questions of database principles]

【数据挖掘复习题】
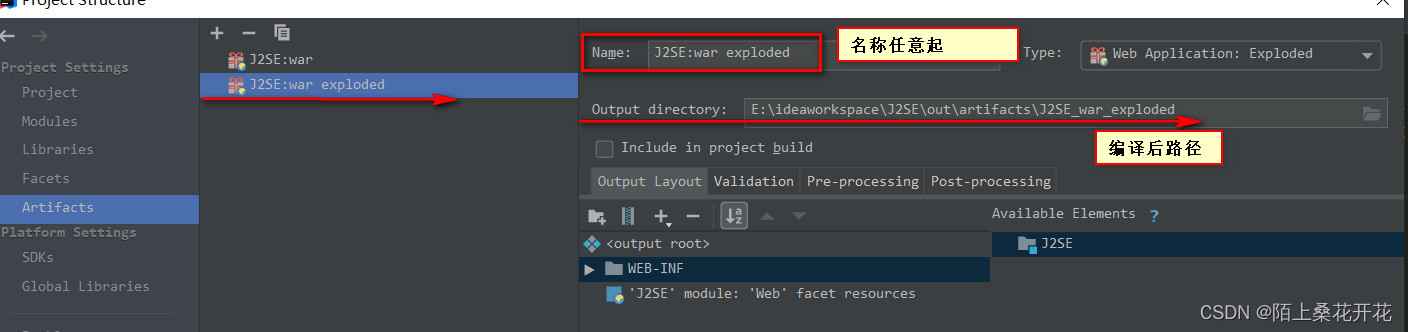
idea将web项目打包成war包并部署到服务器上运行

Idea packages the web project into a war package and deploys it to the server to run

剑指Offer06. 从尾到头打印链表

4. 无线体内纳米网:电磁传播模型和传感器部署要点
随机推荐
GCN thinking - word2vec directly calculates text classification
Application of ncnn Neural Network Computing Framework in Orange Pi 3 Lts Development Board
并网-低电压穿越与孤岛并存分析
Gan totem column bridgeless boost PFC (single phase) seven PFC duty cycle feedforward
十條職場規則
【计网】第三章 数据链路层(2)流量控制与可靠传输、停止等待协议、后退N帧协议(GBN)、选择重传协议(SR)
Solve the problem of VI opening files with ^m at the end
Do you feel like you've learned something and forgotten it?
idea将web项目打包成war包并部署到服务器上运行
Write a simple nodejs script
Official website of Unicode query
Export the entire Oracle Database
Swift Error Handling
[ManageEngine] the role of IP address scanning
Lambda expression
Ali & ant self developed IDE
剑指Offer03. 数组中重复的数字【简单】
Swift5.7 extend some to generic parameters
Recovery of website address and method of Amazon account login two-step verification failure caused by mobile phone number becoming empty
Xctf mobile--app3 problem solving