当前位置:网站首页>Leetcode series (I): buying and selling stocks
Leetcode series (I): buying and selling stocks
2022-07-27 07:06:00 【Mr_ health】
1. The first question is :122. The best time to buy and sell stocks II
Write four methods according to my own progressive thinking , The first three are dynamic programming , The last is greed .
Method 1: Two dimensional dynamic matrix
The idea is to maintain a n*2 Dynamic matrix of ,dp[i][0] It means the first one i Days do not hold the maximum profit of the stock ,dp[i][1] It means the first one i The biggest profit of holding stock in the day . Then there is the transfer equation as follows :
- The first i The biggest profit of holding stock in the day = max( keep i-1 Days holding shares , i-1 Days do not hold shares + Buy today )
- The first i Days do not hold the maximum profit of the stock = max( keep i-1 Days do not hold shares , i-1 Days holding shares + Sell today )
Write the formula :


The code is as follows :
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp =[[0 for i in range(2)] for j in range(n)]
dp[0][1] = -prices[0] # purchase ( hold )
dp[0][0] = 0 # There is no stock in hand ( Don't hold )
for i in range(1,n):
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
return dp[-1][0]python The results of the submission :

Method 2: Two one-dimensional dynamic matrices
The transfer equation is the same , The code is as follows :
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
buy = [0] * n
free = [0] * n
buy[0] = -prices[0]# purchase
for i in range(1,n):
buy[i] = max(buy[i-1], free[i-1] - prices[i])
free[i] = max(free[i-1], buy[i-1] + prices[i])
return free[-1]Submit results , Speed has improved

Method 3: Cancel array
By means of 2 You can see , The first i The second result is only related to i-1 Secondary related , It has nothing to do with the previous , Therefore, we can only keep the previous demerit recording .
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
buy = -prices[0]
free = 0
for i in range(1,n):
buy = max(buy, free - prices[i])
free = max(free, buy + prices[i])
return freeLet's take a look at the code ,buy = max(buy, free - prices[i]) First updated ,free It was updated after . Normally, update free What is used is that of the previous day buy, If buy Update first , that free The update is not from the previous day buy, But today buy. There is no problem with this , Because You can buy and then sell on the same day
Method 4: greedy
The greedy method can be understood in this way , We want maximum profit , It is necessary to make the selling price higher than the buying price , namely prices[latest] > prices[pre]. The minimum cell span we traverse is 1, That is, for adjacent intervals 1, If prices[i+1] > prices[i], We can buy and sell for profit .
This is also based on : You can buy and then sell on the same day .
We want a scene , The price on the first day is 7, The next day's price is 1, Obviously we can't buy on the first day , Sell the next day , It will lose money , So you should buy it the next day . If you start with the first day of buying , So in fact, buying the next day is = One day buy and sell + Buy the next day .
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
profit = 0
for i in range(1,n):
profit += max(0, prices[i] - prices[i-1])
return profit2. The second question is :121. The best time to buy and sell stocks
This question is a little simpler than the previous one , Because only one sale is allowed , And you can't buy or sell on the same day .
Method 1: brutal force
Nest two loops , Slower
Method 2: Two dimensional dynamic matrix
The idea is to maintain a n*2 Dynamic matrix of ,dp[i][0] It means the first one i Days do not hold the maximum profit of the stock ,dp[i][1] It means the first one i The biggest profit of holding stock in the day . Then there is the transfer equation as follows :
- The first i The biggest profit of holding stock in the day = max( keep i-1 Days holding shares , Buy for the first time today )
- The first i Days do not hold the maximum profit of the stock = max( keep i-1 Days do not hold shares , i-1 Days holding shares + Sell today )
The red font is also different from the previous transfer equation , The reason is that you can only buy it once .
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0 for j in range(2)] for i in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0] # hold
for i in range(1,n):
dp[i][1] = max(dp[i-1][1],-prices[i]) # For the first time to buy
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) # sell-out
return dp[-1][0]Method 3: Two one-dimensional dynamic matrices
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
buy = [0] * n
sell = [0] * n
buy[0] = -prices[0]
for i in range(1,n):
buy[i]= max(buy[i-1],-prices[i]) # For the first time to buy
sell[i] = max(sell[i-1], buy[i-1] + prices[i]) # sell-out
return sell[-1]Method 4: Cancel array
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
buy = -prices[0]
sell = 0
for i in range(1,n):
buy= max(buy,-prices[i]) # for the first time
sell = max(sell, buy + prices[i]) # sell-out
return sell边栏推荐
- 【11】 Binary code: "holding two roller handcuffs, crying out for hot hot hot"?
- Boostrap
- deepsort源码解读(六)
- Significance of NVIDIA SMI parameters
- Express框架
- DataScience:数据生成之在原始数据上添加小量噪声(可自定义噪声)进而实现构造新数据(dataframe格式数据存储案例)
- Shell programming specifications and variables
- AI: play games in your spare time - earn it a small goal - [Alibaba security × ICDM 2022] large scale e-commerce map of risk commodity inspection competition
- Web configuration software for industrial control is more efficient than configuration software
- Summary of APP launch in vivo application market
猜你喜欢

MySql数据库

基于SSM实现的校园新闻发布管理系统

Peptide nucleic acid oligomer containing azobenzene monomer (nh2-tnt4, n-pnas) Qiyue biological customization

采用QT进行OpenGL开发(一)绘制平面图形

Reasoning speed of model
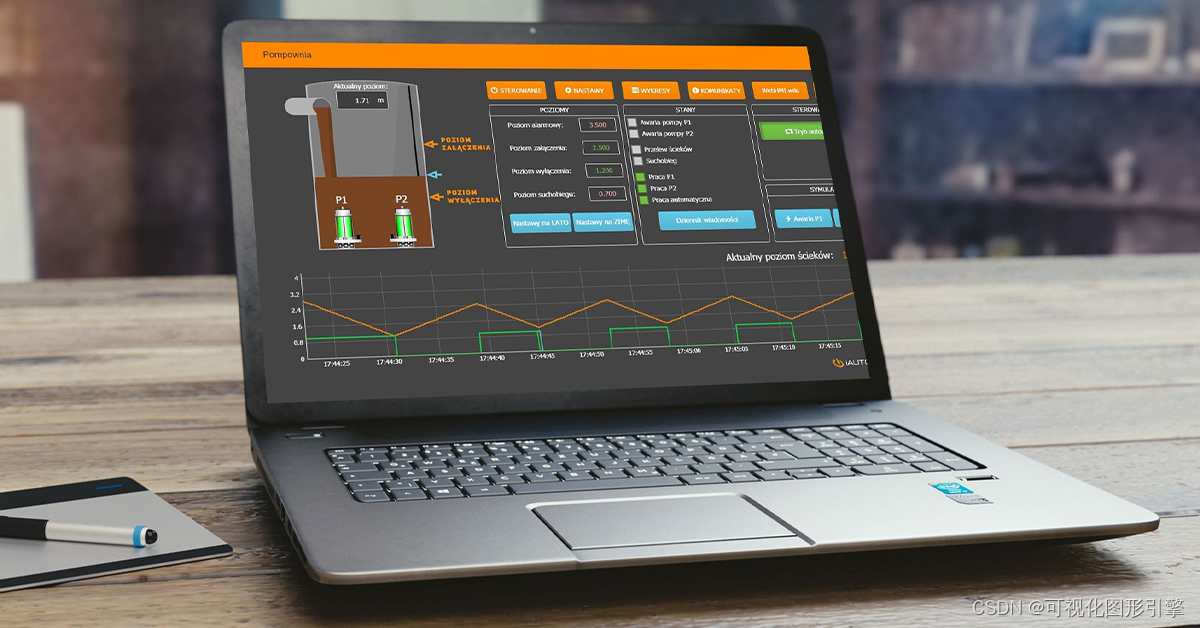
工控用Web组态软件比组态软件更高效

关于ES6的新特性

Hospital reservation management system based on SSM
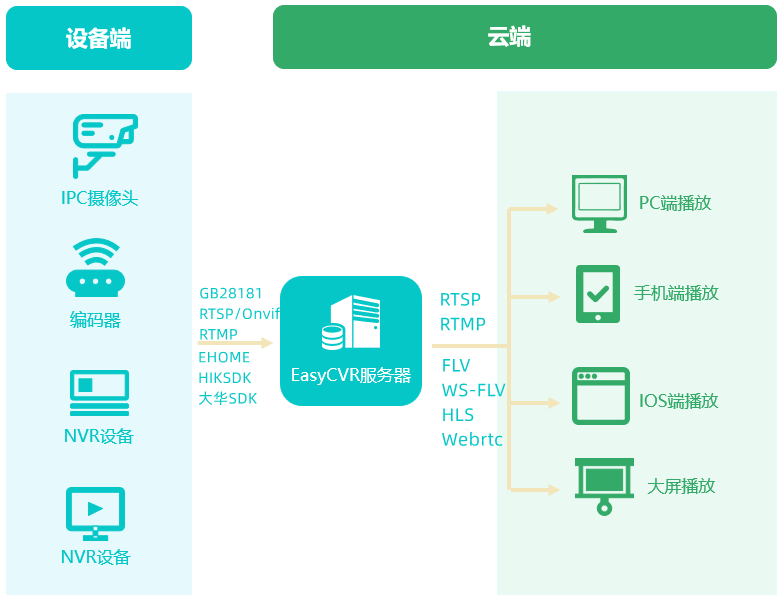
What is the reason why dragging the timeline is invalid when playing device videos on the easycvr platform?

DNA偶联PbSe量子点|近红外硒化铅PbSe量子点修饰脱氧核糖核酸DNA|PbSe-DNA QDs
随机推荐
DNA(脱氧核糖核酸)供应|碳纳米管载核酸-DNA/RNA材料|DNA/RNA核酸修饰磁性纳米颗粒
MySql数据库
Interpretation of deepsort source code (III)
Dsgan degenerate network
工控用Web组态软件比组态软件更高效
Details of cross entropy loss function in pytorch
Boostrap
Qi Yue: thiol modified oligodna | DNA modified cdte/cds core-shell quantum dots | DNA coupled indium arsenide InAs quantum dots InAs DNA QDs
O2O电商线上线下一体化模式分析
脱氧核糖核酸DNA改性近红外二区砷化镓GaAs量子点|GaAs-DNA QDs|DNA修饰GaAs量子点
CentOS上使用Docker安装和部署Redis
Fix the problem that the paging data is not displayed when searching the easycvr device management list page
聊聊大火的多模态
Pymysql query result conversion JSON
AI: play games in your spare time - earn it a small goal - [Alibaba security × ICDM 2022] large scale e-commerce map of risk commodity inspection competition
含有偶氮苯单体的肽核酸寡聚体(NH2-TNT4,N-PNAs)齐岳生物定制
事件捕获方式和冒泡方式—它们的区别是什么?
智能安防视频平台EasyCVR出现通道列表为空情况的原因是什么?
基于SSM学生学籍管理系统
手机上也能训练BERT和ResNet了?!