当前位置:网站首页>力扣62 不同路径(从矩阵左上到右下的所有路径数量) (动态规划)
力扣62 不同路径(从矩阵左上到右下的所有路径数量) (动态规划)
2022-07-07 01:41:00 【裴南苇_】
今天遇到一道个人认为很有价值的动态规划问题。从这道题里,个人感觉对动态规划有了更深刻的了解,大家可以看看对自己又没有帮助。
先看题目:
一个机器人位于一个 m x n 网格的左上角,机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角问总共有多少条不同的路径?
示例
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
解答:
由题目得知,每一次只能向下或者向右移动
由此我们推知 ===》 到达一个格子的路径数量,由它左边格子和上边格子所决定
由此我们推知 ===》 这里可以使用动态规划的思想来解决
由此动态方程 ===》 dp[i][j] = dp[i-1][j] + dp[i][j-1]
至此,我们已经解决一半的问题了,然后我们再思考第一列和第一行,由于每一次只能向下或者向右移动,所以第一行的每个格子都只能由它左边的格子向右移动而来, 所以第一行dp[0][j] 都应该为1,第一列格子同理。
至此分析结束,列出代码
public int uniquePaths(int m, int n) {
int[][] dp = new int [m][n];
for(int i=0;i<n;i++){
dp[0][i] = 1;
}
for(int i=0;i<m;i++){
dp[i][0] = 1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
好了,这次的文章就到这里,喜欢的同学可以点赞收藏,遇到问题,可以评论,或者留言,我一定会第一时间给到回馈,感谢观看!!
注:本文为本人学习时心得分享,有讲错或者需要改正的地方,请指正,我会虚心接受
边栏推荐
- JVM监控及诊断工具-命令行篇
- Jstat pour la commande JVM: voir les statistiques JVM
- Ctfshow-- common posture
- 苹果cms V10模板/MXone Pro自适应影视电影网站模板
- The boss always asks me about my progress. Don't you trust me? (what do you think)
- Bypass open_ basedir
- JVM monitoring and diagnostic tools - command line
- "Parse" focalloss to solve the problem of data imbalance
- 当我们谈论不可变基础设施时,我们在谈论什么
- On the discrimination of "fake death" state of STC single chip microcomputer
猜你喜欢
【SQL实战】一条SQL统计全国各地疫情分布情况
![[FPGA] EEPROM based on I2C](/img/28/f4f2efda4b5feb973c9cf07d9d908f.jpg)
[FPGA] EEPROM based on I2C
ML's shap: Based on the adult census income binary prediction data set (whether the predicted annual income exceeds 50K), use the shap decision diagram combined with the lightgbm model to realize the
一名普通学生的大一总结【不知我等是愚是狂,唯知一路向前奔驰】

VMware安装后打开就蓝屏

你不知道的互联网公司招聘黑话大全
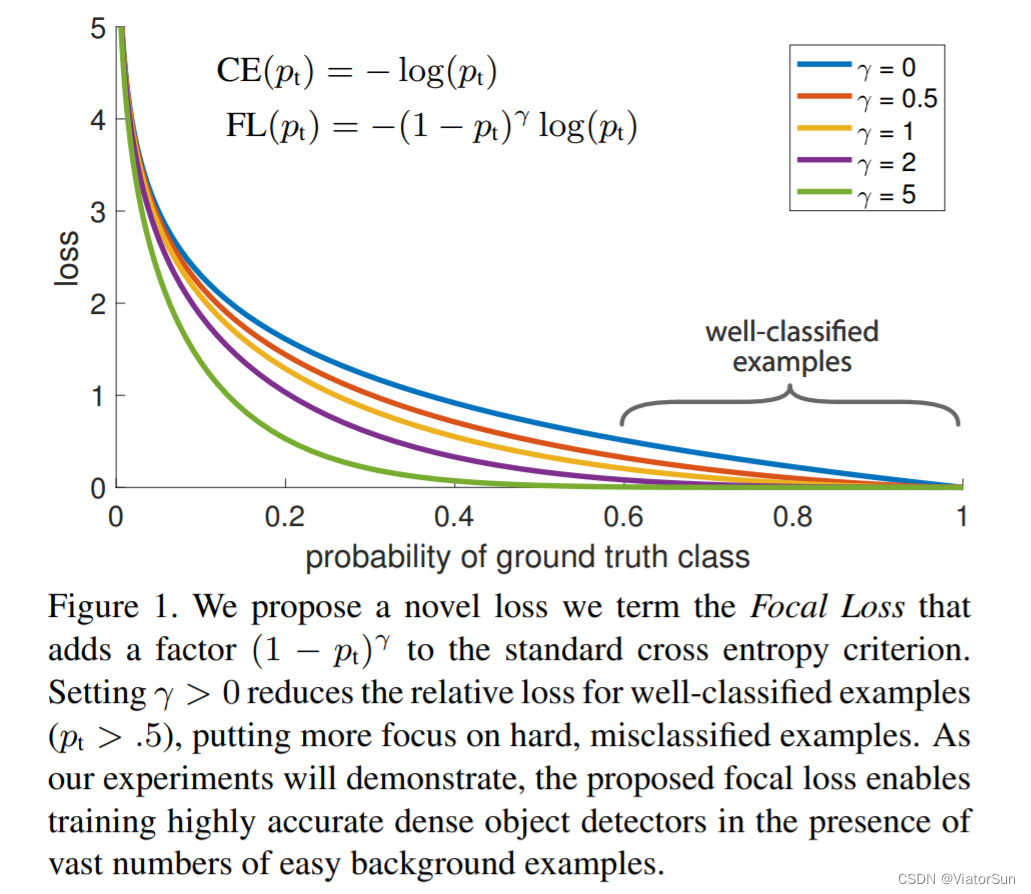
「解析」FocalLoss 解决数据不平衡问题

Understand the deserialization principle of fastjson for generics
C note 13

JVM monitoring and diagnostic tools - command line
随机推荐
PowerPivot - DAX (function)
Check point: the core element for enterprises to deploy zero trust network (ztna)
C language sorting (to be updated)
jvm命令之 jcmd:多功能命令行
[SOC FPGA] peripheral PIO button lights up
You don't know the complete collection of recruitment slang of Internet companies
From "running distractor" to data platform, Master Lu started the road of evolution
进程间通信之共享内存
Career experience feedback to novice programmers
Jstack of JVM command: print thread snapshots in JVM
Jmeter自带函数不够用?不如自己动手开发一个
Calculation model FPS
JVM命令之 jstat:查看JVM统计信息
[SQL practice] a SQL statistics of epidemic distribution across the country
JVM monitoring and diagnostic tools - command line
外设驱动库开发笔记43:GPIO模拟SPI驱动
基于ADAU1452的DSP及DAC音频失真分析
10W word segmentation searches per second, the product manager raised another demand!!! (Collection)
Solve pod install error: FFI is an incompatible architecture
Financial risk control practice - decision tree rule mining template