当前位置:网站首页>「解析」FocalLoss 解决数据不平衡问题
「解析」FocalLoss 解决数据不平衡问题
2022-07-07 01:26:00 【ViatorSun】
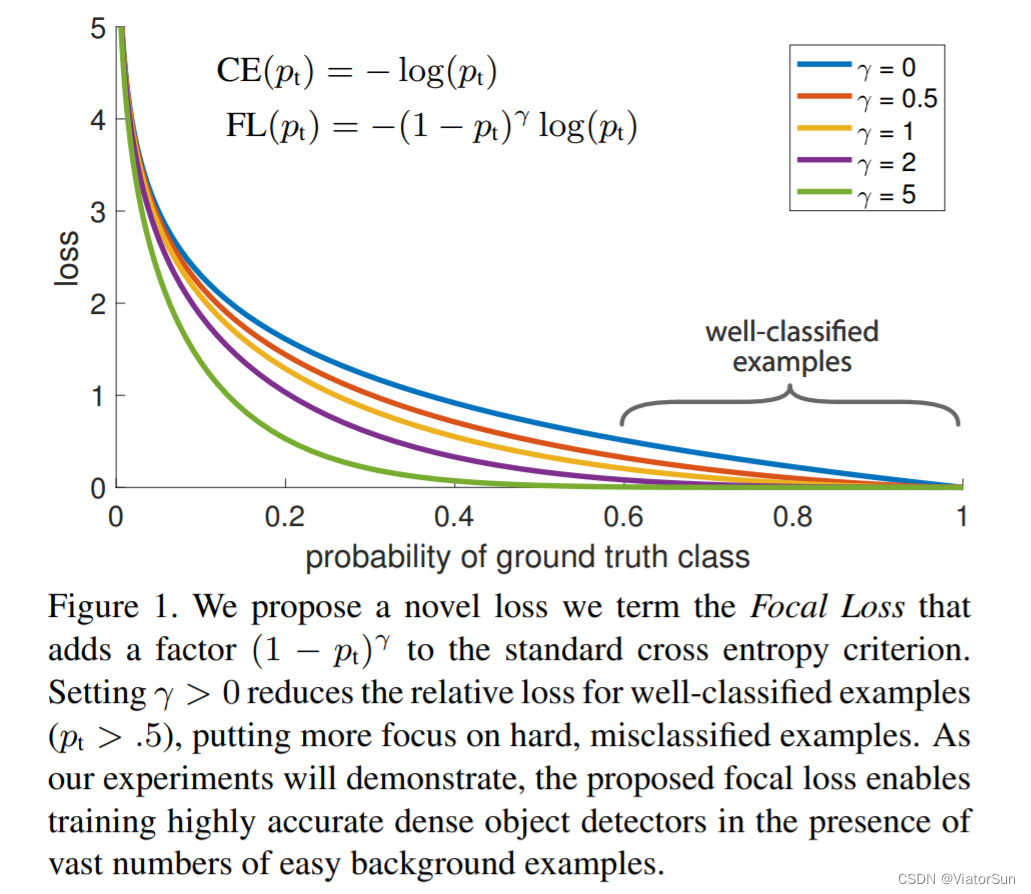
FocalLoss 的出现,主要是为了解决 anchor-based (one-stage) 目标检测网络的分类问题。后面实例分割也常使用。
注意
这里是 目标检测网络的分类问题,而不是单纯的分类问题,这两者是不一样的。
区别在于,对于分配问题,一个图片一定是属于某一确定的类的;而检测任务中的分类,是有大量的anchor无目标的(可以称为负样本)。
分类任务
正常的 K类分类任务 的标签,是用一个K长度的向量作为标签,用one-hot(或者+smooth,这里先不考虑)来进行编码,最终的标签是一个形如[1,…, 0, …, 0]这样的。那么如果想要将背景分离出,自然可以想到增加一个1维,如果目标检测任务有K类,这里只要用K+1维来表示分类,其中1维代表无目标即可。对于分类任务而言,最后一般使用 softmax 来归一,使得所有类别的输出加和为1。
但是在检测任务中,对于无目标的anchor,我们并不希望最终结果加和为1,而是所有的概率输出都是0。 那么可以这样,我们将一个多分类任务看做多个二分类任务(sigmoid),针对每一个类别,我输出一个概率,如果接近0则代表非该类别,如果接近1,则代表这个anchor是该类别。
所以网络输出不需要用softmax来归一,而是对K长度向量的每一个分量进行sigmoid激活,让其输出值代表二分类的概率。对于无目标的anchor,gt中所有的分量都是0,代表属于每一类的概率是0,即标注为背景。
至此,FocalLoss解决的问题不是多分类问题,而是 多个二分类问题。
公式解析
首先看公式:只有 标签 y = 1 y=1 y=1时,公式/交叉熵才有意义, p t p_t pt即为标签为1时对应的预测值/模型分类正确的概率
p t = ( 1 − p r e d _ s i g m o i d ) ∗ t a r g e t + p r e d _ s i g m o i d ∗ ( 1 − t a r g e t ) p_t = (1 - pred\_sigmoid) * target + pred\_sigmoid * (1 - target) pt=(1−pred_sigmoid)∗target+pred_sigmoid∗(1−target)
C E ( p t ) = − α t log ( p t ) F L ( p t ) = − α t ( 1 − p t ) γ log ( p t ) F L ( p ) = { − α ( 1 − p ) γ log ( p ) , i f y = 1 − ( 1 − α ) p γ log ( 1 − p ) , i f y = 0 CE(p_t)=-\alpha_t \log(p_t) \\ \quad \\ FL(p_t)=-\alpha_t(1-p_t)^\gamma \log(p_t) \\ \quad \\ FL(p) = \begin{cases} \quad -\alpha(1-p)^\gamma \log(p) &, if \quad y=1 &\\ -(1-\alpha)p^\gamma \log(1-p)&,if \quad y=0 \end{cases} CE(pt)=−αtlog(pt)FL(pt)=−αt(1−pt)γlog(pt)FL(p)={ −α(1−p)γlog(p)−(1−α)pγlog(1−p),ify=1,ify=0
- 参数p[公式3]:当 p->0时(概率很低/很难区分是那个类别),调制因子 (1-p)接近1,损失不被影响,当 p->1时,(1-p)接近0,从而减小易分样本对总 loss的贡献
- 参数 γ \gamma γ:当 γ = 0 \gamma=0 γ=0 时,Focal loss就是传统的交叉熵,
当 γ \gamma γ 增加时, 调节系数 ( 1 − p t ) (1-p_t) (1−pt) 也会增加。
当 γ \gamma γ 为定值时,比如 γ = 2 \gamma=2 γ=2 ️对于easy example(p>0.5) p=0.9 的loss要比标准的交叉熵小 100倍,当 p=0.968时,要小1000+倍;️对于 hard example(p<0.5) loss要小4倍
这样的话, hard example 的权重相对提升了很多,从而增加了哪些误分类的重要性。
实验表明, γ = 2 , α = 0.75 \gamma=2,\alpha=0.75 γ=2,α=0.75时效果最好 - α \alpha α 调节正负样本不平衡系数, γ \gamma γ 控制难易样本不平衡
代码复现
在官方给的代码中,并没有 target = F.one_hot(target, num_clas) 这行代码,这是因为
# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
import torch
from torch.nn import functional as F
def sigmoid_focal_loss( inputs: torch.Tensor, targets: torch.Tensor, alpha: float = -1,
gamma: float = 2, reduction: str = "none") -> torch.Tensor:
inputs = inputs.float()
targets = targets.float()
p = torch.sigmoid(inputs)
target = F.one_hot(target, num_clas+1)
ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction="none")
p_t = p * targets + (1 - p) * (1 - targets)
loss = ce_loss * ((1 - p_t) ** gamma)
if alpha >= 0:
alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
loss = alpha_t * loss
if reduction == "mean":
loss = loss.mean()
elif reduction == "sum":
loss = loss.sum()
return loss
sigmoid_focal_loss_jit: "torch.jit.ScriptModule" = torch.jit.script(sigmoid_focal_loss)
此外,torchvision 中也支持 focal loss
完整代码
官方完整代码:https://github.com/facebookresearch/
参考
- https://zhuanlan.zhihu.com/p/391186824
边栏推荐
- Check Point:企业部署零信任网络(ZTNA)的核心要素
- What is make makefile cmake qmake and what is the difference?
- 高并发大流量秒杀方案思路
- Data storage 3
- Understand the deserialization principle of fastjson for generics
- Detailed explanation of platform device driver architecture in driver development
- mac版php装xdebug环境(m1版)
- POI excel export, one of my template methods
- ML's shap: Based on the adult census income binary prediction data set (whether the predicted annual income exceeds 50K), use the shap decision diagram combined with the lightgbm model to realize the
- vim映射大K
猜你喜欢

为不同类型设备构建应用的三大更新 | 2022 I/O 重点回顾
测试开发基础,教你做一个完整功能的Web平台之环境准备
Digital IC interview summary (interview experience sharing of large manufacturers)

Bbox regression loss function in target detection -l2, smooth L1, IOU, giou, Diou, ciou, focal eiou, alpha IOU, Siou

The boss always asks me about my progress. Don't you trust me? (what do you think)
Jstat pour la commande JVM: voir les statistiques JVM
![[InstallShield] Introduction](/img/df/4522d06510ff918d00659b8358368f.jpg)
[InstallShield] Introduction
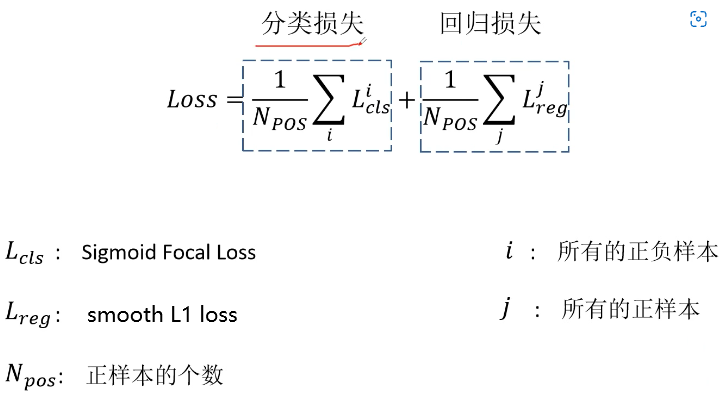
Loss function and positive and negative sample allocation in target detection: retinanet and focal loss
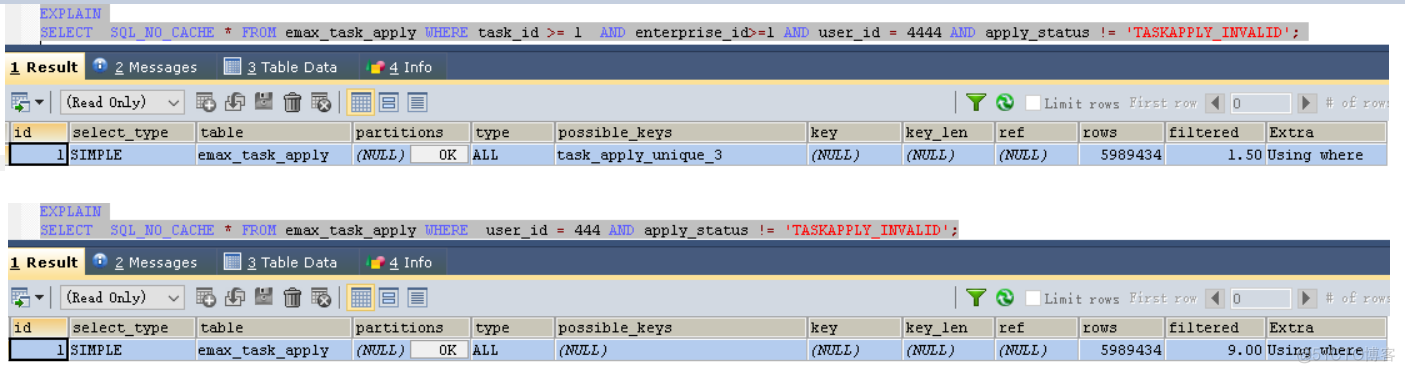
Say sqlyog deceived me!
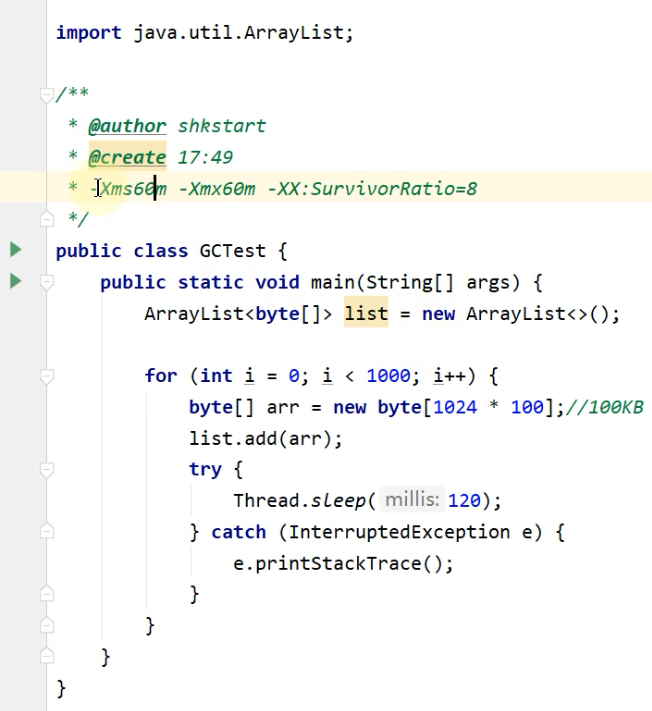
JVM命令之- jmap:导出内存映像文件&内存使用情况
随机推荐
进程间通信之共享内存
从“跑分神器”到数据平台,鲁大师开启演进之路
Deep clustering: joint optimization of depth representation learning and clustering
Bypass open_ basedir
Jstat pour la commande JVM: voir les statistiques JVM
Interview questions and salary and welfare of Shanghai byte
10W word segmentation searches per second, the product manager raised another demand!!! (Collection)
每秒10W次分词搜索,产品经理又提了一个需求!!!(收藏)
[SQL practice] a SQL statistics of epidemic distribution across the country
Question 102: sequence traversal of binary tree
693. 行程排序
测试开发基础,教你做一个完整功能的Web平台之环境准备
JVM command - jmap: export memory image file & memory usage
mac版php装xdebug环境(m1版)
window下面如何安装swoole
Value range of various datetimes in SQL Server 2008
Nvisual network visualization
Crudini 配置文件编辑工具
Redisl garbled code and expiration time configuration
【GNN】图解GNN: A gentle introduction(含视频)