Eating grapes
Learning algorithms depends on routines , Identify labuladong That's enough !
If you're facing autumn moves , Dongge tells you something The routine in the written examination .

Related to recommend :
After reading this article , You can go and get the following questions :
-----------
Today, I did a piece called 「 Eat grapes 」 The subject of , Very interesting .
There are three kinds of grapes , Each one has a, b, c star , Now there are three people , The first man only ate the first and second grapes , The second man only ate the second and third grapes , The third man only ate the first and third grapes .
Now I'll give you the input a, b, c Three values , Please arrange it properly , Let three people eat all the grapes , The algorithm returns How many grapes should the most people eat .
Topic link :
https://www.nowcoder.com/questionTerminal/14c0359fb77a48319f0122ec175c9ada
The title form and force of Niu Ke net are different , I remove input and output processing , The core of the topic is to let you implement such a function :
// Input the number of grapes of three kinds , It could be very big , So use long type
// Return to eat the most people to eat at least how many grapes
long solution(long a, long b, long c);
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
title
First of all, let's understand the topic , How do you make 「 The man who eats the most eats the least 」?
It can be understood in this way , We don't care about the restriction that everyone can only eat two specific grapes , How do you make 「 The man who eats the most eats the least 」?
obviously , Just average the score , Everyone eats (a+b+c)/3 Grapes . Even if you can't divide , for instance a+b+c=8, That also needs to be as average as possible , It means eating alone 2 star , The other two eat 3 star .
Sum up ,「 The man who eats the most eats the least 」 Let's divide it as evenly as possible , And the number of grapes eaten by the person who eats the most is (a+b+c)/3 The result of rounding up , That is to say (a+b+c+2)/3.
PS: Rounding up is a common algorithmic technique . In most programming languages , If you want to calculate M Divide N,M / N It's going to round down , If you want to round up , You can change to (M+(N-1)) / N.
Okay , I was just talking about a simple situation , Now consider if you add 「 Everyone can only eat two kinds of grapes 」 The limitation of , How do you do it? ?
in other words , Everyone can only eat two kinds of grapes , You have to As far as possible Divide equally among three people , So that the person who eats the most eats the least .
It's complicated , If you use X, Y, Z It means these three people , You'll find that they form a triangle :
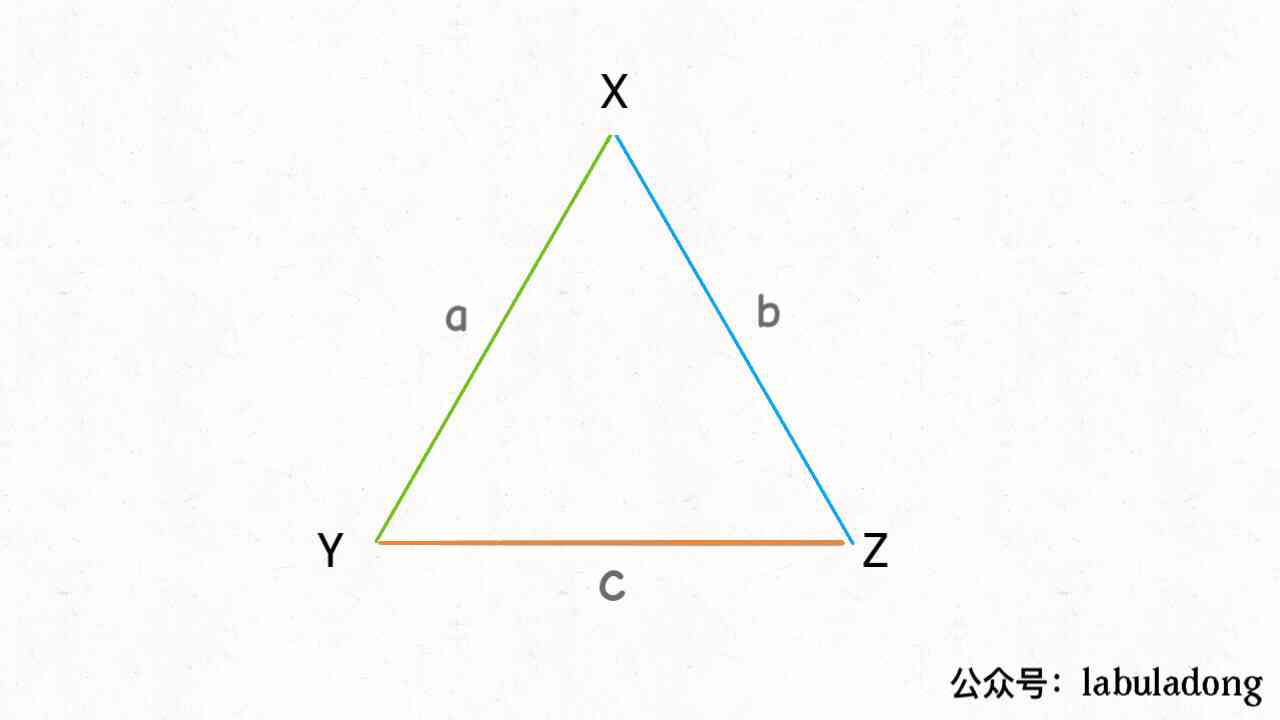
You make someone eat a certain kind of grape more , There will be a cascade effect , Thinking about it is a headache , How about that ?
Thought analysis
Anyway, everything depends on exhaustion , I started thinking about the possibility of brutality in backtracking algorithms :
For every grape , Who might have eaten it ? There are two possibilities , So I write a backtracking algorithm , List all the possibilities , And find the best value, OK ?
It's theoretically possible , But the complexity of brute force algorithms is usually exponential , If you take grapes as 「 Lead 」 To exhaust , Look at the variables a, b, c All are long Data of type , This complexity has made my spine furrow in cold sweat .
Well, this problem still has to be ingenious , The idea still has to go back to how 「 Distribute as evenly as possible 」 above , Then things get interesting .
If you count the grapes a, b, c As three lines , Their size is the length of the line , Think about what geometry they might form ? Whether our purpose can be translated into 「 Divide the perimeter of the geometry as evenly as possible 」?
A graph of three lines , That's a triangle ? Don't worry , We have learned , The triangle is to satisfy that the sum of the two sides is greater than the third side , hypothesis a < b < c, Well, there are two situations :
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
If a + b > c, So you can make a triangle , Just take the midpoint of each side , We can divide the circumference of the triangle into three parts , And each copy contains two sides :
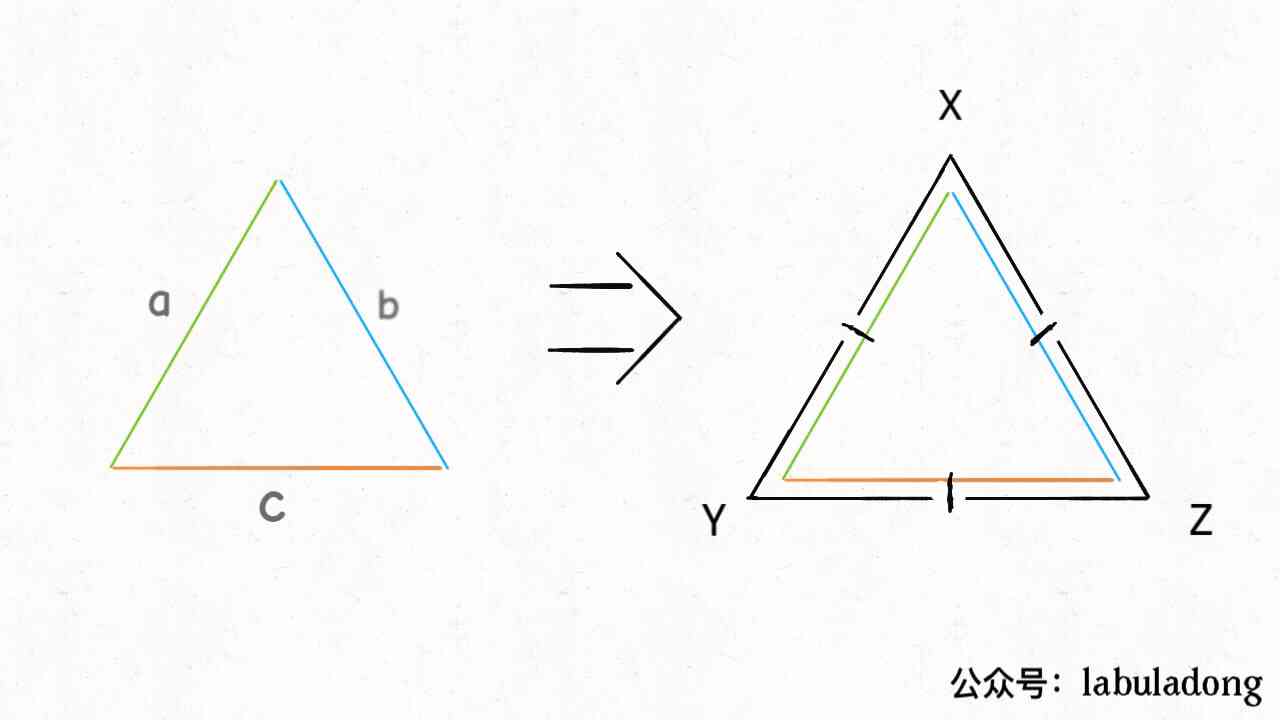
in other words , In this case , Three people are still able to divide all the grapes equally , The minimum number of grapes that people who eat the most can still eat is (a+b+c+2)/3.
If a + b <= c, These three edges can't form a closed figure , So we can put the longest side c「 break 」, That is to form a quadrilateral .
There are two situations :
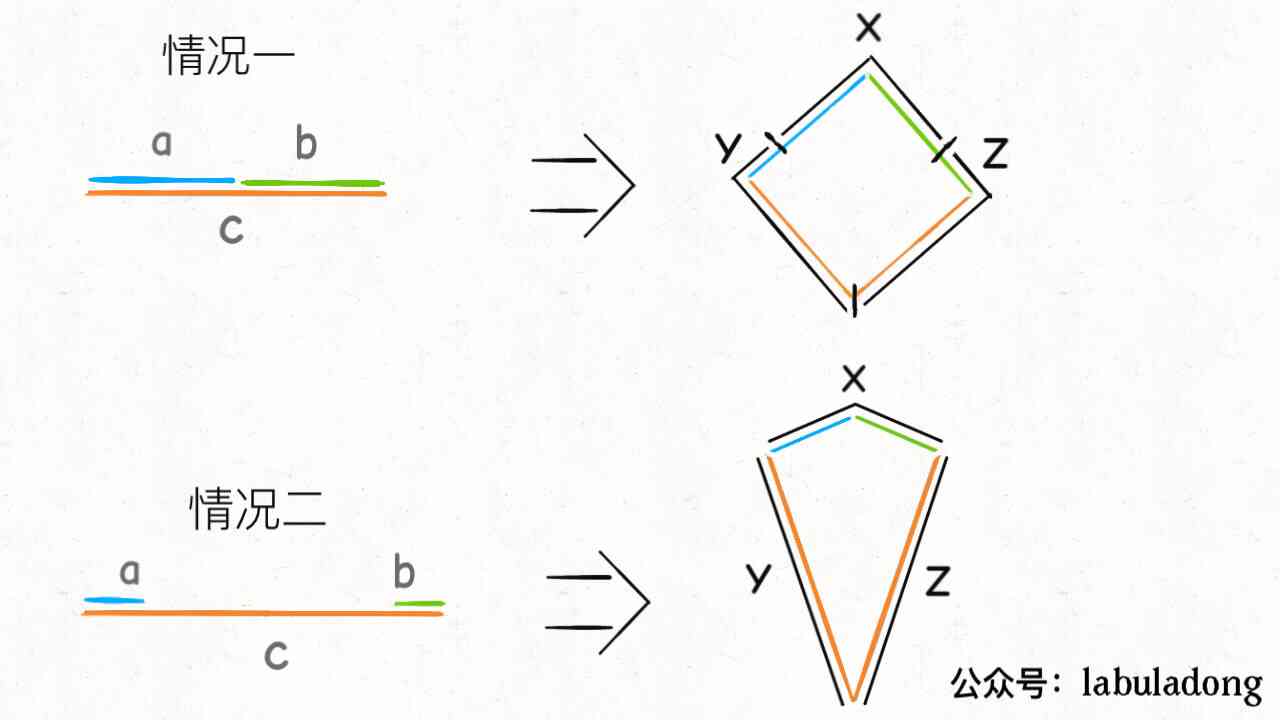
For case one ,a + b and c When the gap is not big , You can see that it still allows three people to divide the quadrilateral equally , So the least grapes that people who eat the most can still eat (a+b+c+2)/3.
With c The increase of , There will be situation two , here c > 2*(a+b), Because everyone's taste is limited , In order to share as much as possible ,X Eat at most a and b, and c The edge needs to be Y or Z divide equally , That is to say, at this time, the person who eats the most can eat at least the number of grapes (c+1)/2, That is to divide equally c Edge up round .
That's all , The code translates as follows :
long solution(long a, long b, long c) {
long[] nums = new long[]{a, b, c};
Arrays.sort(nums);
long sum = a + b + c;
// Can form a triangle , It can be divided equally
if (nums[0] + nums[1] > nums[2]) {
return (sum + 2) / 3;
}
// Can't make a triangle , In the case of bisecting the longest side
if (2 * (nums[0] + nums[1]) < nums[2]) {
return (nums[2] + 1) / 2;
}
// Can't make a triangle , But it's still possible to divide it equally
return (sum + 2) / 3;
}
thus , The problem was solved skillfully , The time complexity is just O(1), The key idea is how to divide as much as possible .
Who would have thought , Eating a grape depends on Geometry ? Maybe that's the charm of algorithms ...
_____________
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ! Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star !