当前位置:网站首页>高斯推断推导
高斯推断推导
2022-08-03 23:58:00 【威士忌燕麦拿铁】
设有一对服从多元正态分布的变量 ( x , y ) (\boldsymbol{x}, \boldsymbol{y}) (x,y),可以写出他们的联合概率密度函数:
p ( x , y ) = N ( [ μ x μ y ] , [ Σ x x Σ x y Σ y x Σ y y ] ) p(\boldsymbol{x}, \boldsymbol{y})=\mathcal{N}\left(\left[\begin{array}{l}\boldsymbol{\mu}_{x} \\\boldsymbol{\mu}_{y}\end{array}\right],\left[\begin{array}{ll}\boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\\boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y}\end{array}\right]\right) p(x,y)=N([μxμy],[ΣxxΣyxΣxyΣyy])
其中, Σ y x = Σ x y T \boldsymbol{\Sigma}_{y x}=\boldsymbol{\Sigma}_{x y}^{\mathrm{T}} Σyx=ΣxyT。
由舒尔补有:
[ Σ x x Σ x y Σ y x Σ y y ] = [ 1 Σ x y Σ y y − 1 0 1 ] [ Σ x x − Σ x y Σ y y − 1 Σ y x 0 0 Σ y y ] [ 1 0 Σ y y − 1 Σ y x 1 ] \left[\begin{array}{cc}\boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\\boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y}\end{array}\right]=\left[\begin{array}{cc}\mathbf{1} & \boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \\\mathbf{0} & \mathbf{1}\end{array}\right]\left[\begin{array}{cc}\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} & \mathbf{0} \\\mathbf{0} & \boldsymbol{\Sigma}_{y y}\end{array}\right]\left[\begin{array}{cc}\mathbf{1} & \mathbf{0} \\\boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} & \mathbf{1}\end{array}\right] [ΣxxΣyxΣxyΣyy]=[10ΣxyΣyy−11][Σxx−ΣxyΣyy−1Σyx00Σyy][1Σyy−1Σyx01]
对两边同时求逆有:
[ Σ x x Σ x y Σ y x Σ y y ] − 1 = [ 1 0 − Σ y y − 1 Σ y x 1 ] [ ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 0 0 Σ y y − 1 ] [ 1 − Σ x y Σ y y − 1 0 1 ] {\left[\begin{array}{cc}\boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\\boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y}\end{array}\right]^{-1}= \left[\begin{array}{cc}\mathbf{1} & \mathbf{0} \\-\boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} & \mathbf{1}\end{array}\right]} \left[\begin{array}{cc}\left(\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right)^{-1} & \boldsymbol{0} \\\boldsymbol{0} & \boldsymbol{\Sigma}_{y y}^{-1}\end{array}\right]\left[\begin{array}{cc}\mathbf{1} & -\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \\\mathbf{0} & \mathbf{1}\end{array}\right] [ΣxxΣyxΣxyΣyy]−1=[1−Σyy−1Σyx01][(Σxx−ΣxyΣyy−1Σyx)−100Σyy−1][10−ΣxyΣyy−11]
因此,联合概率密度函数 p ( x , y ) p(\boldsymbol{x}, \boldsymbol{y}) p(x,y) 指数部分的二次项为:
( [ x y ] − [ μ x μ y ] ) T [ Σ x x Σ x y Σ y x Σ y y ] − 1 ( [ x y ] − [ μ x μ y ] ) = ( [ x y ] − [ μ x μ y ] ) T [ 1 0 − Σ y y − 1 Σ y x 1 ] [ ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 0 0 Σ y y − 1 ] × [ 1 − Σ x y Σ y y − 1 0 1 ] ( [ x y ] − [ μ x μ y ] ) = ( x − μ x − Σ x y Σ y y − 1 ( y − μ y ) ) T ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 × ( x − μ x − Σ x y Σ y y − 1 ( y − μ y ) ) + ( y − μ y ) T Σ y y − 1 ( y − μ y ) \begin{aligned}&\left(\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]-\left[\begin{array}{l}\boldsymbol{\mu}_{x} \\\boldsymbol{\mu}_{y}\end{array}\right]\right)^{\mathrm{T}}\left[\begin{array}{ll}\boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\\boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y}\end{array}\right]^{-1}\left(\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]-\left[\begin{array}{l}\boldsymbol{\mu}_{x} \\\boldsymbol{\mu}_{y}\end{array}\right]\right) \\=&\left(\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]-\left[\begin{array}{l}\boldsymbol{\mu}_{x} \\\boldsymbol{\mu}_{y}\end{array}\right]\right)^{\mathrm{T}}\left[\begin{array}{cc}\boldsymbol{1} & \boldsymbol{0} \\-\boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} & \boldsymbol{1}\end{array}\right]\left[\begin{array}{cc}\left(\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right)^{-1} & \boldsymbol{0} \\\mathbf{0} & \boldsymbol{\Sigma}_{y y}^{-1}\end{array}\right] \\& \times\left[\begin{array}{cc}\mathbf{1} & -\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \\\mathbf{0} & \mathbf{1}\end{array}\right]\left(\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]-\left[\begin{array}{l}\boldsymbol{\mu}_{x} \\\boldsymbol{\mu}_{y}\end{array}\right]\right) \\=&\left(\boldsymbol{x}-\boldsymbol{\mu}_{x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right)\right)^{\mathrm{T}}\left(\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right)^{-1} \\& \times\left(\boldsymbol{x}-\boldsymbol{\mu}_{x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right)\right)+\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right)^{\mathrm{T}} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right)\end{aligned} ==([xy]−[μxμy])T[ΣxxΣyxΣxyΣyy]−1([xy]−[μxμy])([xy]−[μxμy])T[1−Σyy−1Σyx01][(Σxx−ΣxyΣyy−1Σyx)−100Σyy−1]×[10−ΣxyΣyy−11]([xy]−[μxμy])(x−μx−ΣxyΣyy−1(y−μy))T(Σxx−ΣxyΣyy−1Σyx)−1×(x−μx−ΣxyΣyy−1(y−μy))+(y−μy)TΣyy−1(y−μy)
很明显可以看出,这是两个二次项的和。
又由贝叶斯公式有:
p ( x , y ) = p ( x ∣ y ) p ( y ) p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y}) p(x,y)=p(x∣y)p(y)
并且:
p ( y ) = N ( μ y , Σ y y ) p(\boldsymbol{y}) =\mathcal{N}\left(\boldsymbol{\mu}_{y}, \boldsymbol{\Sigma}_{y y}\right) p(y)=N(μy,Σyy)
因此,由幂运算中同底数幂相乘,底数不变、指数相加的性质,可以得到:
p ( x ∣ y ) = N ( μ x + Σ x y Σ y y − 1 ( y − μ y ) , Σ x x − Σ x y Σ y y − 1 Σ y x ) p(\boldsymbol{x} \mid \boldsymbol{y}) =\mathcal{N}\left(\boldsymbol{\mu}_{x}+\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right), \boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right) p(x∣y)=N(μx+ΣxyΣyy−1(y−μy),Σxx−ΣxyΣyy−1Σyx)
这便是高斯推断中最重要的部分:从状态的先验概率分布出发,然后基于一些观测值来缩小这个范围。
边栏推荐
- Unity intercepts 3D images and the implementation of picture-in-picture PIP
- Creo 9.0二维草图的诊断:加亮开放端点
- 响应式织梦模板塑身瑜伽类网站
- 2022年8月份DAMA-CDGA/CDGP数据治理认证招生简章
- 2022-08-03: What does the following go code output?A: 2; B: 3; C: 1; D: 0.package main import "fmt" func main() { slice := []i
- 射频芯片(RFIC)的协议之5G及其调制
- 并查集详解
- Using matlab to solve the linear optimization problem based on matlab dynamic model of learning notes _11 】 【
- 【每日一题】899. 有序队列
- (PC+WAP)织梦模板螺钉手柄类网站
猜你喜欢
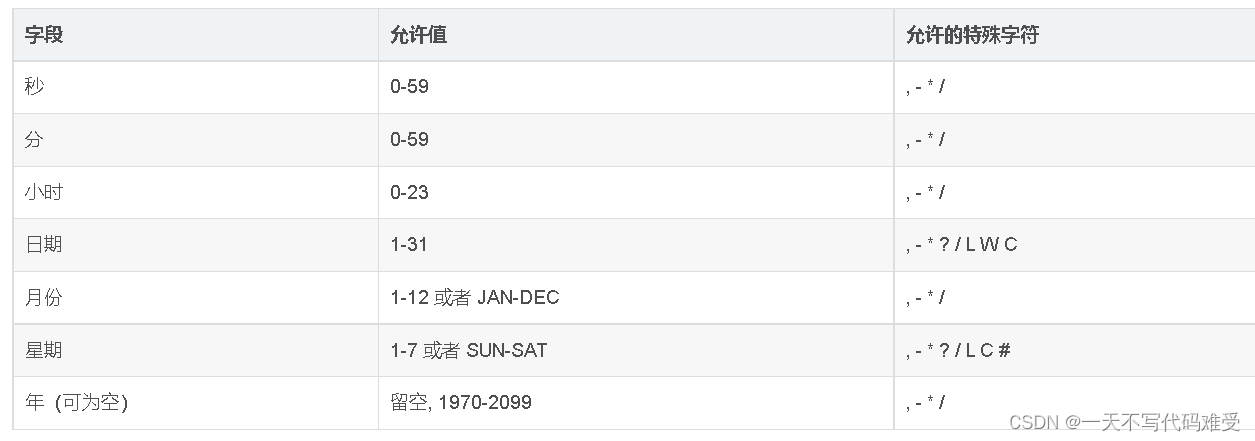
corn表达式 具体详解与案例
![2022-08-03:以下go语言代码输出什么?A:2;B:3;C:1;D:0。 package main import “fmt“ func main() { slice := []i](/img/a9/6de3c2bae92d09b13b1c36e01f86c2.png)
2022-08-03:以下go语言代码输出什么?A:2;B:3;C:1;D:0。 package main import “fmt“ func main() { slice := []i
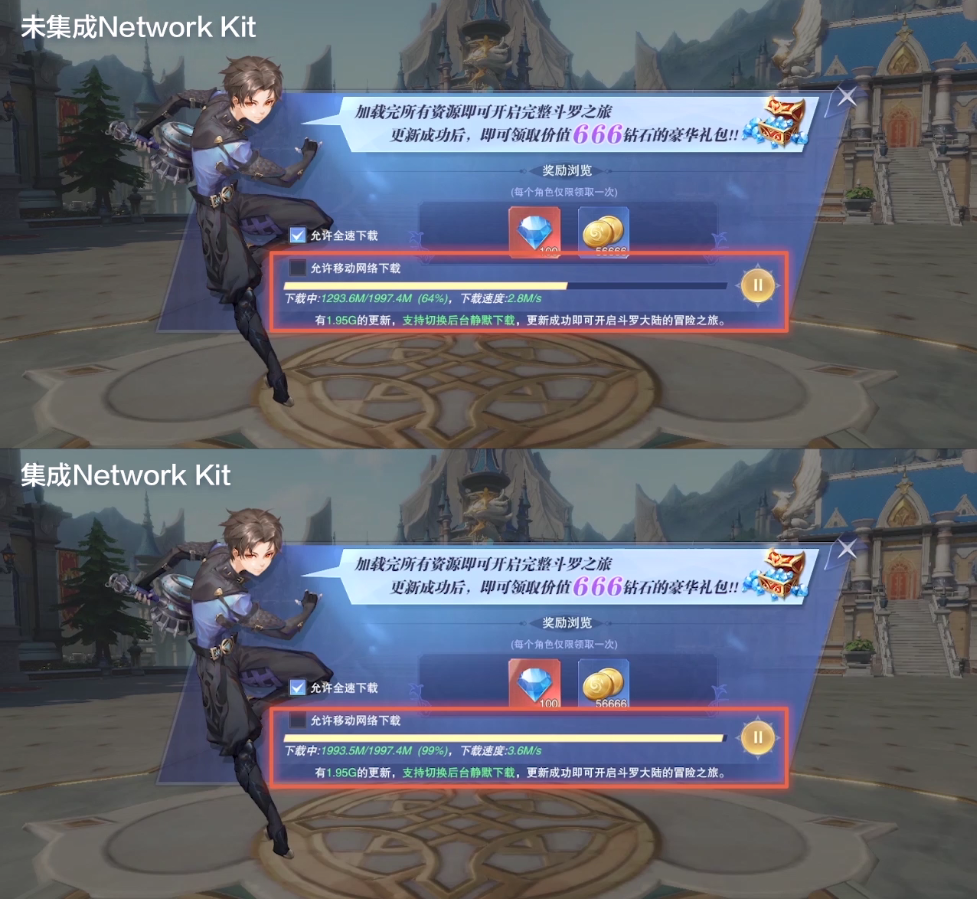
The Chinese Valentine's Day event is romantically launched, don't let the Internet slow down and miss the dark time

响应式织梦模板除尘器类网站
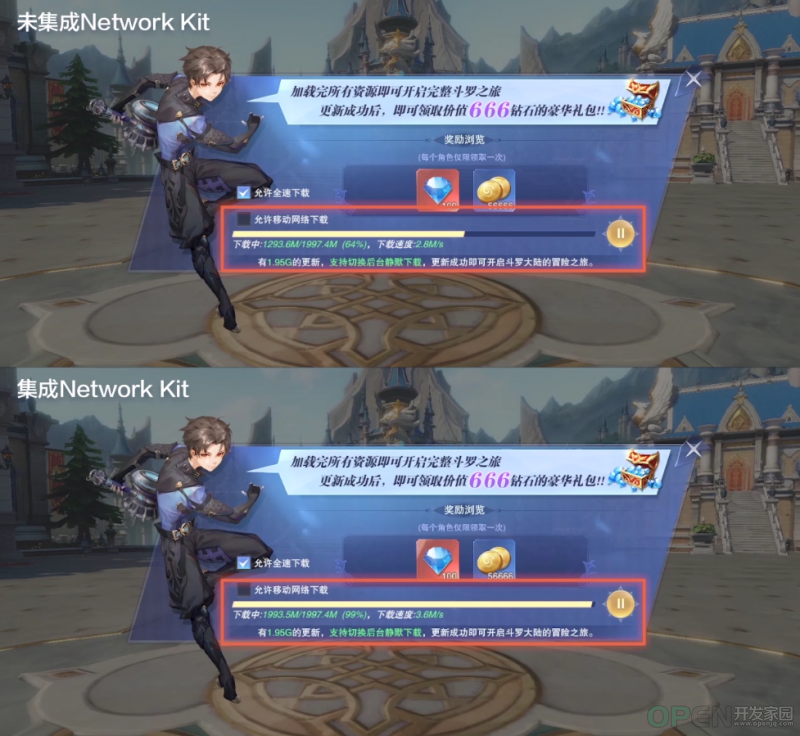
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
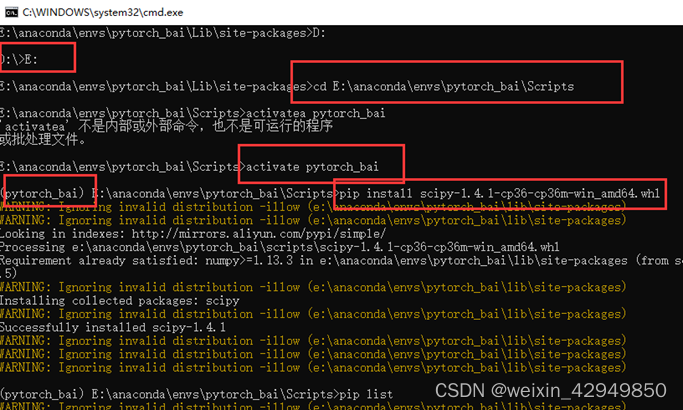
通过whl安装第三方包
Nanoprobes Alexa Fluor 488 FluoroNanogold 偶联物
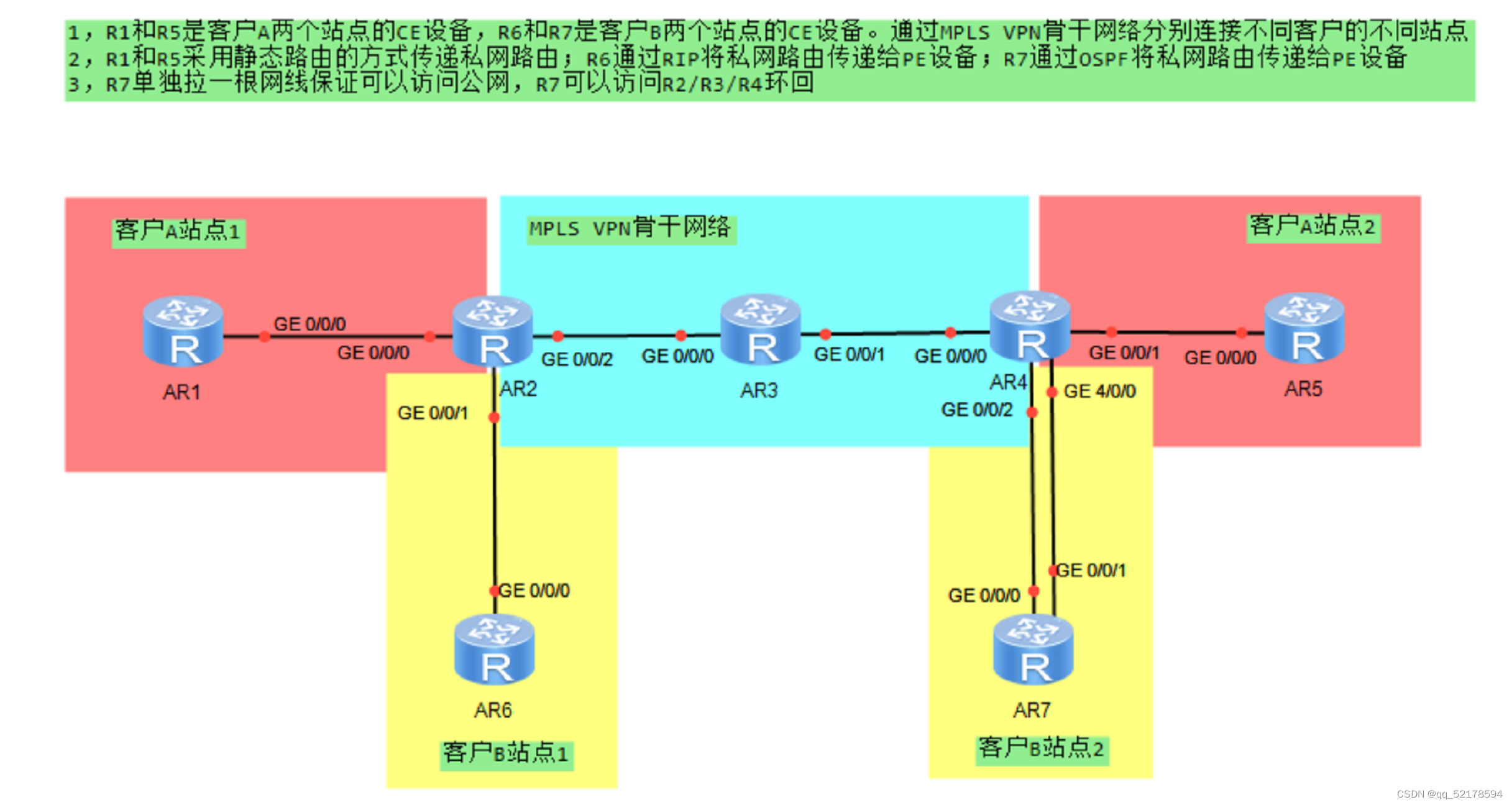
MPLS Comprehensive Experiment
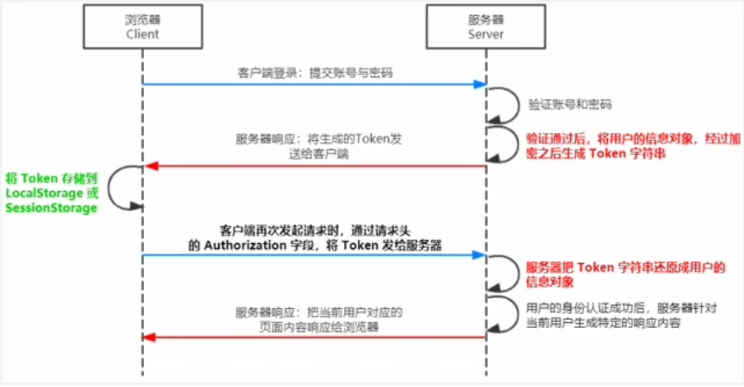
Node.js的基本使用(三)数据库与身份认证

全球首款量产,获定点最多!这家AVP Tier1如何实现领跑?
随机推荐
2021年数据泄露成本报告解读
【OpenCV图像处理】 图像拼接技术
- the skip/skipif Pytest learning
【杂项】通过Excel为字符串产生条码
Minimized installation of debian11
【LeetCode】最长公共子序列(动态规划)
Jar a key generation document database
After building the pytorch environment, the pip and conda commands cannot be used
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
curl使用指南
电子邮件安全或面临新威胁!
A simple understanding of TCP, learn how to shake hands, wave hands and various states
corn表达式 具体详解与案例
Install third-party packages via whl
Super perfect version of the layout have shortcut, background replacement (solve the problem of opencv Chinese path)
利用matlab求解线性优化问题【基于matlab的动力学模型学习笔记_11】
【LeetCode】最长回文子序列(动态规划)
北京电竞元宇宙论坛活动顺利召开
孙宇晨:Web3.0和元宇宙将协助人类更加全面地进入网络世界
Graph-node:创建一个新的subgraph