当前位置:网站首页>Learn tla+ (XII) -- functions through examples
Learn tla+ (XII) -- functions through examples
2022-07-05 01:41:00 【Liu Xiaojing】
Functions and examples
function
TLA+ In addition to Numbers , character string , Boolean value , Model value 4 There are two basic types , There are also two complex types , Set and function . Functions form the basis of all practical complex types .
The form of the function looks the same as the operators introduced before . There are two ways to define functions :
Function == [s \in S |-> foo] \* here foo It can be any equation . Notice I'm using theta |->, No :
Function[s \in S] == foo
Infinite sets can be used in function definitions , Such as
Doubles == [n \in Nat |-> 2*n ]
Doubles[12] = 24 \* The call mode is [], instead of ()
\* multi-parameter
Sum == [x, y \in 1..10 |-> x + y] \* Limit the x,y The value of the 1..10 in
Sum[2,3] = 5
Sum[2,30] \* error,30 be not in 1..10 in
Addx(x) == [y \in Nat |-> x+y+1]
Addx(2)[3] = 6 \* This call x=2,y=3
Set of functions
The syntax of the function set is :SetOfFunctions == [A -> B], Notice I'm using theta -> , instead of |->. -> The result of needs to be used |-> To describe . for example :
S1 == {1, 2}
S2 == {3, 4}
[s \in S1 |-> S2] = [1 |-> {3, 4}, 2 |-> {3, 4}] = <<{3,4},{3,4}>> \* This is a tuple
[S -> S] = {[1 |-> 3, 2 |-> 3], [1 |-> 3, 2 |-> 4], [1 |-> 4, 2 |-> 3], [1 |-> 4, 2 |-> 4]} = {<<3, 3>>, <<3, 4>>, <<4, 3>>, <<4, 4>>} \* This is a collection ,[1 |-> 3, 2 |-> 3] Medium 1 Represents the first element ,2 For the second element , If you will 1,2 Replace with 2,3, It cannot be expressed as <<3,3>> 了 , It can only be expressed as [2|->3,3|->3]
example
1、 Given a string , Returns the number of each character . Such as : Given <<“a”,“b”,“a”>> return [a |-> 2, b |-> 1]
\* 1 Convert tuples into sets , At this time, the set contains elements of non repeating tuples 2 Traversing set elements , Count the number of each element in the tuple
Range(S) == {S[t]:t \in 1..Len(S)}
Counter(str) == [c \in Range(str) |-> Cardinality({n \in 1..Len(str) : str[n] = c})]
Counter(<<"a","b","a">>) = [a |-> 2, b|-> 1]
2、 Given a set S And number N, return N individual S Cartesian product of , Such as Op(S, 3) == S \X S \X S
Op(S,N) == [1..N -> S]
边栏推荐
- JS implementation determines whether the point is within the polygon range
- One plus six brushes into Kali nethunter
- Mysql database | build master-slave instances of mysql-8.0 or above based on docker
- pytorch fine-tuning (funtune) : 镂空设计or 偷梁换柱
- Include rake tasks in Gems - including rake tasks in gems
- 流批一体在京东的探索与实践
- Jcenter () cannot find Alibaba cloud proxy address
- The server time zone value ‘� й ��� ʱ 'is unrecognized or representatives more than one time zone【
- Wechat applet: new independent backstage Yuelao office one yuan dating blind box
- Flutter 2.10 update details
猜你喜欢

A simple SSO unified login design
微信小程序:最新wordpress黑金壁纸微信小程序 二开修复版源码下载支持流量主收益
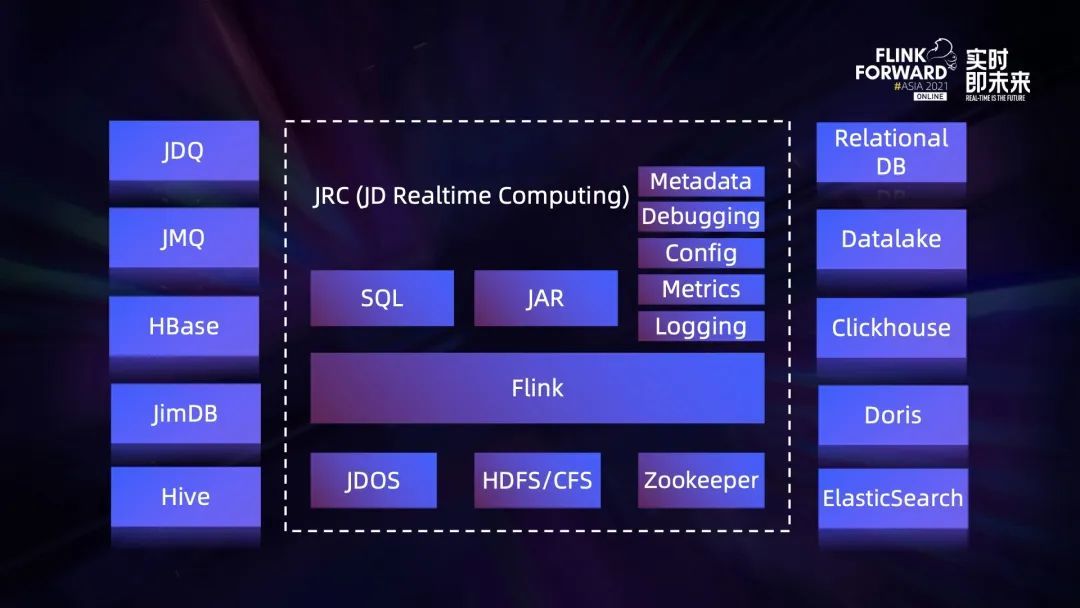
流批一体在京东的探索与实践

MySQL regexp: Regular Expression Query
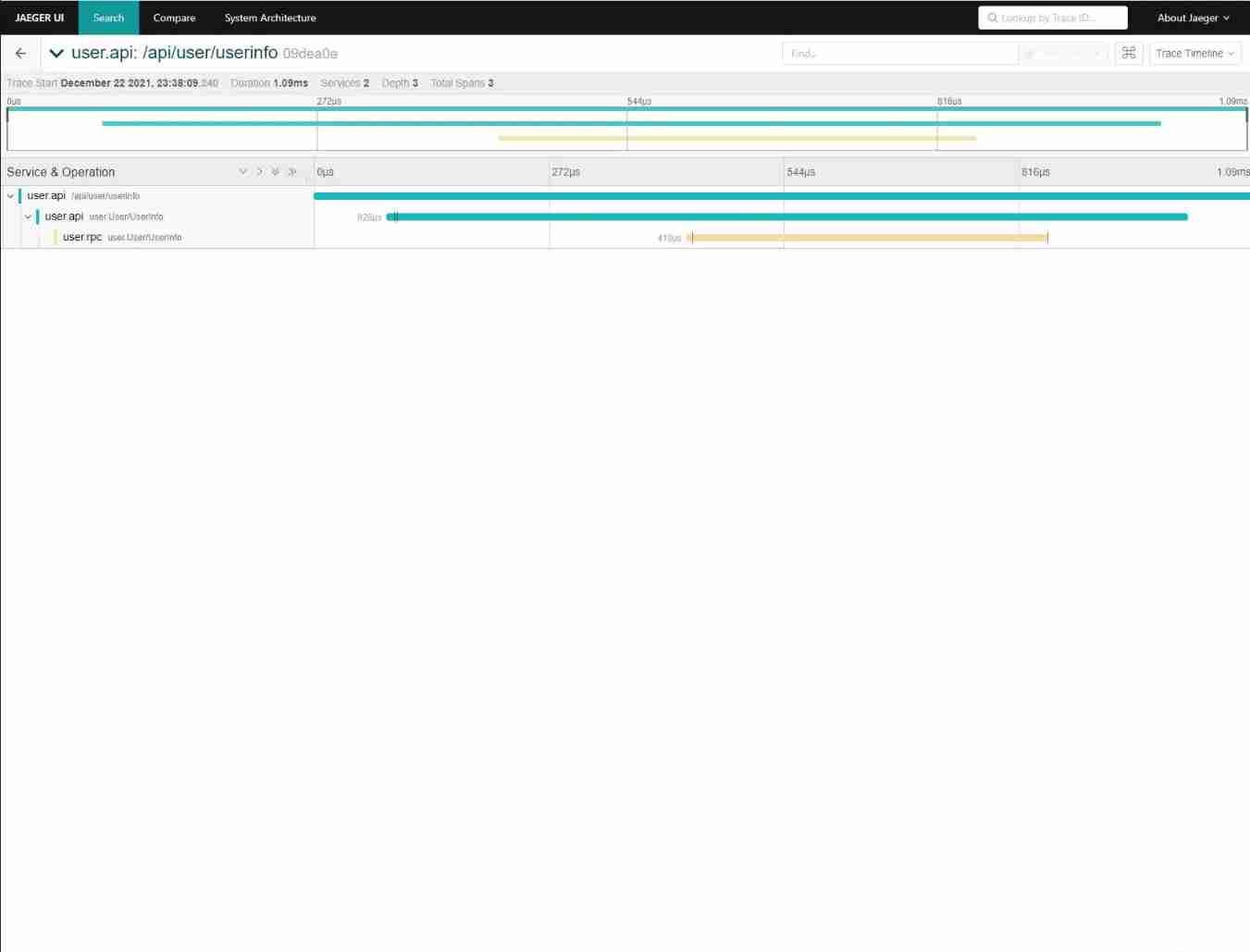
Take you ten days to easily complete the go micro service series (IX. link tracking)

Exploration and practice of integration of streaming and wholesale in jd.com
![[flutter topic] 64 illustration basic textfield text input box (I) # yyds dry goods inventory #](/img/1c/deaf20d46e172af4d5e11c28c254cf.jpg)
[flutter topic] 64 illustration basic textfield text input box (I) # yyds dry goods inventory #
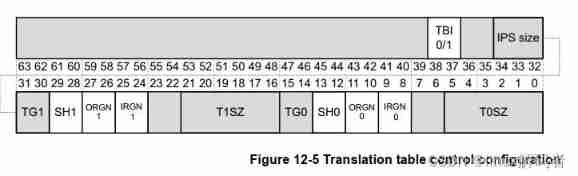
Armv8-a programming guide MMU (3)

Wechat applet: the latest WordPress black gold wallpaper wechat applet two open repair version source code download support traffic main revenue
MATLB|多微电网及分布式能源交易
随机推荐
I use these six code comparison tools
流批一體在京東的探索與實踐
Global and Chinese market of veterinary thermometers 2022-2028: Research Report on technology, participants, trends, market size and share
【LeetCode】88. Merge two ordered arrays
[CTF] AWDP summary (WEB)
One plus six brushes into Kali nethunter
Heartless sword English translation of Xi Murong's youth without complaint
Hand drawn video website
Five ways to query MySQL field comments!
Database postragesq peer authentication
Package What is the function of JSON file? What do the inside ^ angle brackets and ~ tilde mean?
What sparks can applet container technology collide with IOT
Flutter 2.10 update details
Database postragesql lock management
Nebula Importer 数据导入实践
Can financial products be redeemed in advance?
【大型电商项目开发】性能压测-性能监控-堆内存与垃圾回收-39
Global and Chinese market of network connected IC card smart water meters 2022-2028: Research Report on technology, participants, trends, market size and share
The perfect car for successful people: BMW X7! Superior performance, excellent comfort and safety
Global and Chinese markets for stratospheric UAV payloads 2022-2028: Research Report on technology, participants, trends, market size and share