5V串口接3.3V单片机串口怎么搞？

写在前面：两个单片机由于电平不同，串口通信可能会失败，这时候需要通过电平转换电路来解决，本文给出了两种方法，一种是通过三极管搭建，另一种是MOS管搭建，在硬件工程师的笔试中也经常会出现这样的题目。

3.3V单片机和5V单片机通信的思路

3.3V单片机	通信方向	5V单片机
发送逻辑1（对应电压3.3V）	→	接受逻辑1（对应电压5V）
发送逻辑0（对应电压0V）	→	接受逻辑0（对应电压0V）
接受逻辑1（对应电压3.3V）	←	发送逻辑1（对应电压5V）
接受逻辑0（对应电压0V）	←	发送逻辑0（对应电压0V）

MOS管转换电路

工作原理：

1、当3V3单片机发送逻辑1，即3V3_TX=3.3V，Ugs=0V，MOS管截止，5V_RX通过R2上拉到+5V，5V_RX=5V；

2、当3V3单片机发送逻辑0，即3V3_TX=0V，Ugs=3V，MOS管导通，5V_RX会被拉低，5V_RX=0V；

3V3_TX发送给5V_RX

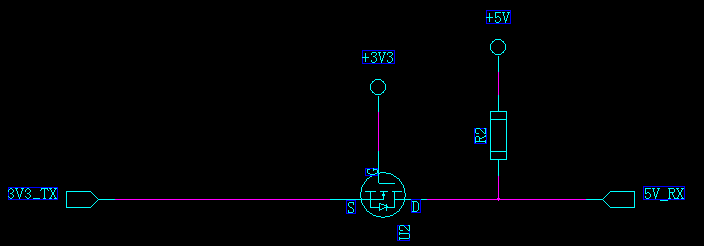
那有人说了，5V的数据怎么发送给3V3单片机呢？是不是将信号方向及电源更换即可，我们来看一下。

工作原理：

1、当5V单片机发送逻辑1，即5V_TX=5V，Ugs=0V，MOS管截止，3V3_RX通过R1上拉到3V3，3V3_RX=3.3V；

2、当5V单片机发送逻辑0，即5V_TX=0V，Ugs=5V，MOS管导通，3V3_RX被拉低，所以3V3_RX=0；

以上分析似乎合情合理，其实如下电路不可用，上面的第2点其实是没有问题的，主要是第1点，当MOS管截止时，5V_TX的5V电压会经过MOS管的体二极管到达3V3_RX，使3V3_RX的电压高于3.3V（4V多，取决于体二极管的导通压降）。这样的话，一方面4V多的电压与3.3V有压差，经过R1电阻会有耗电；另一方面，4V多的电压也可能损坏3.3V单片机的RX管脚。

此电路不可用

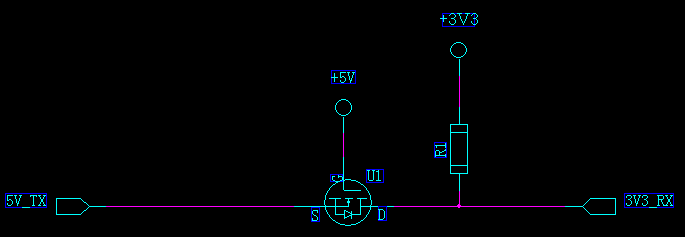
利用仿真软件仿真，可以看到MOS管截止时，输出是4.44V，明显高于3.3V，验证了上述的观点。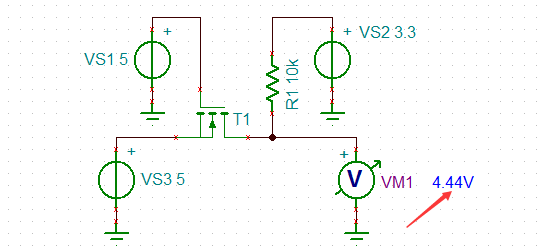

仿真上述不可用电路

那如何设计5V发送到3.3V单片机呢？其实也简单，两个器件搞定，如下是电路图。

1、5V_TX=5V时，二极管D1截止，3V3_RX=3.3V；

2、5V_TX=0V时，二极管D1导通，3V3_RX≈0.6V；实际3V3_RX是多少，取决于D1的正向导通压降，因为要得到更低的电压，一般D1选择肖特基二极管，肖特基优点就是导通压降小。

5V_TX发送给3V3_RX

三极管转换电路

工作原理：

1、当3V3单片机发送逻辑1，即3V3_TX=3.3V，NPN三极管截止，5V_RX通过R2上拉到+5V，5V_RX=5V；

2、当3V3单片机发送逻辑0，即3V3_TX=0V，NPN三极管导通，5V_RX会被拉低，所以5V_RX=0V；

3V3_TX发送给5V_RX

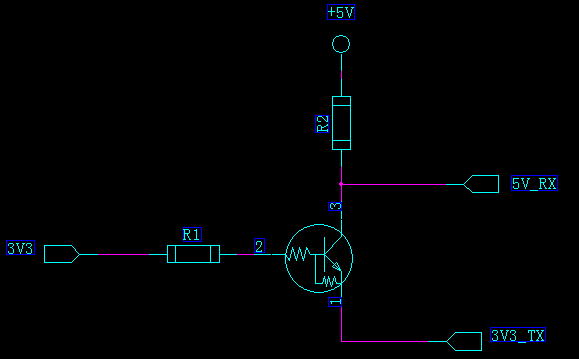
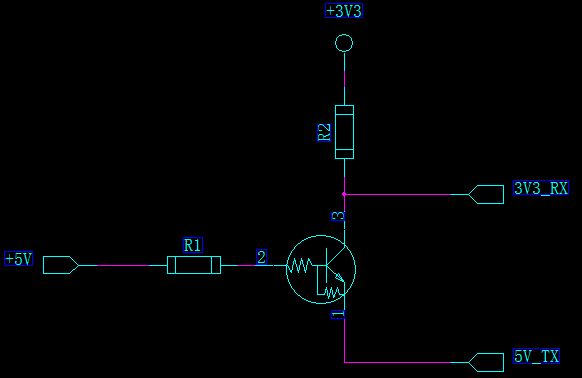
利用三极管，5V单片机发送给3.3V单片机，是不是电源和信号互换就可以，和MOS管电路一样，如下电路同样不能用。

原因是当5V_TX为5V时，发射极反偏，但是5V通过电阻R1由三极管的基极到达三极管的集电极，造成集电极正偏，和MOS管电路一样，使3V3_RX电压高于3.3V（4V多），大家可以仿真一下，这里我就不仿真了。

此电路不可用

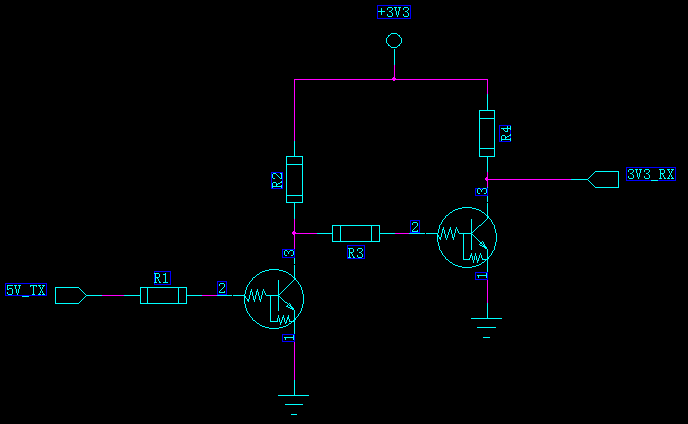
如下，给出了5V单片机向3.3V单片机发送的电路图，用两个NPN三极管搭建。

工作原理：

1、当5V单片机发送逻辑1，即5V_TX=5V，Q1导通，Q2的基极被拉低，Q2截止，所以3V3_RX=3.3V；

2、当5V单片机发送逻辑0，即5V_TX=0V，Q1截止，Q2导通，所以3V3_RX=0V；

5V_TX发送给3V3_RX

可以看到，我并没有画两个NMOS管搭建5V单片机向3.3V单片机发送的电路，其实将上图中的三极管换成NMOS管，就能实现，在实际的电路设计中，为减少成本，应尽量考虑用较少的器件搭电路，所以一般就用二极管方案。

今天的文章到这里就结束了。。。

---

哦不，上面的问题并没有结束

我转发这篇文章的原因是晚上和朋友讨论到这个问题，我们还因为这个问题开了个腾讯会议。

如果要连接的是3.3V的单片机串口，我们第一时间应该想到我们也用3.3V的单片机，两个3.3V的单片机供电上肯定是不会有问题的。而现在市面上很多ARM芯片，都是3.3V的GPIO口电压，5V单片机作为初级入门电平，已经慢慢被取代，当然，之后还有1.8V的单片机。

—— The End ——