当前位置:网站首页>【滤波跟踪】基于matlab扩展卡尔曼滤波EKF和无迹卡尔曼滤波UKF比较【含Matlab源码 1933期】
【滤波跟踪】基于matlab扩展卡尔曼滤波EKF和无迹卡尔曼滤波UKF比较【含Matlab源码 1933期】
2022-07-07 09:46:00 【海神之光】
一、获取代码方式
获取代码方式1:
完整代码已上传我的资源:【滤波跟踪】基于matlab扩展卡尔曼滤波EKF和无迹卡尔曼滤波UKF比较【含Matlab源码 1933期】
获取代码方式2:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
备注:订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、EKF算法简介
在SLAM问题解决方法中,EKF算法是比较常用的经典算法。机器人的自定位过程是一个非线性化的过程,EKF是为了解决Kalman滤波器不能应用于非线性系统而产生的,该滤波算法的主要过程是预测和更新。在预测和更新过程中,EKF算法对原有的系统方程和观测方程进行线性化并得到一个高估计的结果。如果系统中的非线性很弱,EKF也能给出很好的估计结果。
预测时,使用系统模型如下:
式中,z(k+1)表示的是第k+1步中获得的观测量,W (k+1)表示Kalman增益,其中还包括了前向估计在实际中的权重。
实现EKF-SLAM需要以下几方面内容:系统动态方程以及相应的参量,使用的传感器类型和观测方程,根据这些可以得到EKF的相应形式。二维平面中的EKF-SLAM需要知道机器人在X、Y方向的值,还需要知道二维平面下机器人头部朝向与X轴正方向的夹角。
三、部分源代码
%% 主函数功能:EKF与UKF误差分析,性能比较
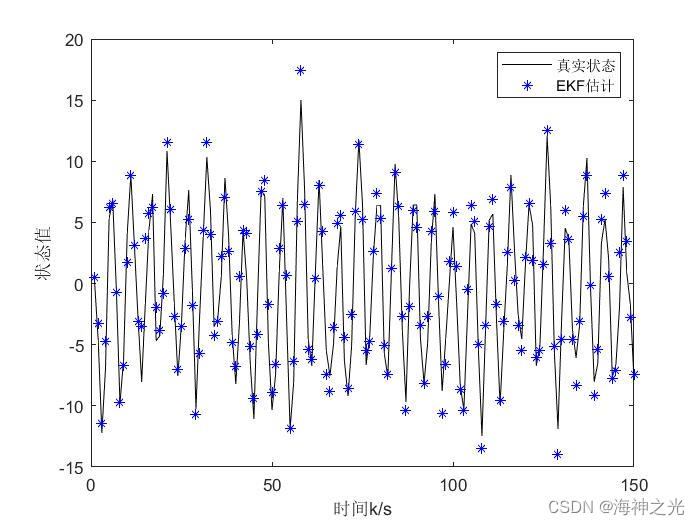
%图一:真实状态和EKF滤波状态比较
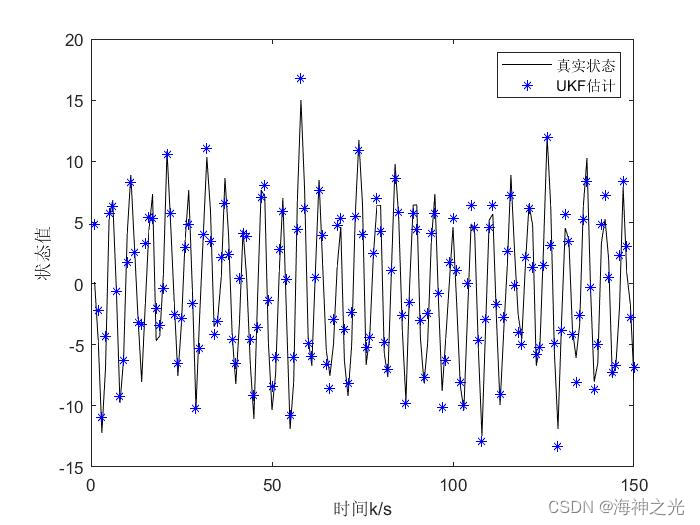
%图二:真实状态和UKF滤波状态比较
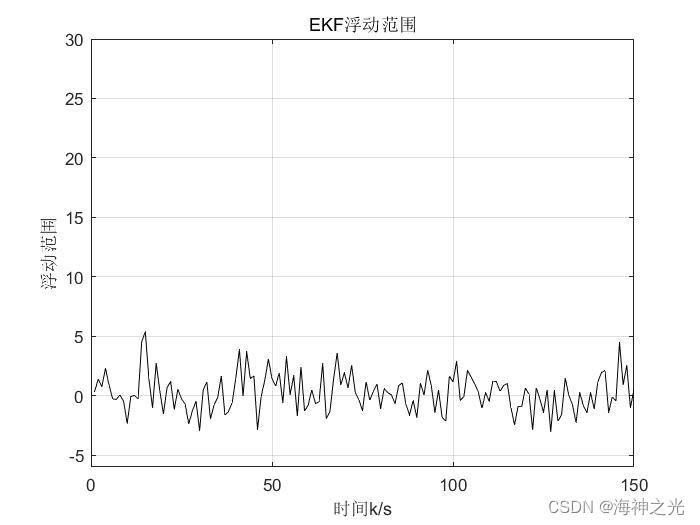
%图三:EKF滤波误差浮动范围
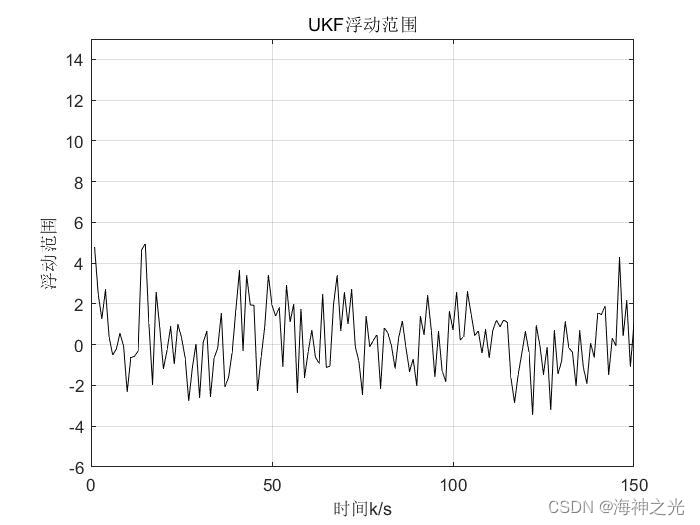
%图四:UKF滤波误差浮动范围
N=150; %仿真时间
L=1;
Q=6; %噪声方差
R=1;
W=sqrtm(Q)*randn(L,N);
V=sqrt(R)*randn(1,N);
X=zeros(L,N);
X(:,1)=[0.1]';
Z=zeros(1,N);
Z(1)=X(:,1)^2/20+V(1);
Xukf=zeros(L,N);
Xukf(:,1)=X(:,1)+sqrtm(Q)*randn(L,1);
Pukf=eye(L);
Xekf=zeros(L,N);
Xekf(:,1)=X(:,1)+sqrtm(Q)*randn(L,1);
Pekf=eye(L);
%算法仿真验证
for k=2:N
X(:,k)=0.5*X(:,k-1)+2.5*X(:,k-1)/(1+X(:,k-1)^2)+8*cos(1.2*k)+W(k);
Z(k)=X(:,k)^2/20+V(k);
[Xekf(:,k),Pekf]=EKF(Xekf(:,k-1),Pekf,Z(k),Q,R,k);
[Xukf(:,k),Pukf]=UKF(Xukf(:,k-1),Pukf,Z(k),Q,R,k);
end
四、运行结果
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社,2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社,2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社,2018.
[4]林志东.基于扩展卡尔曼滤波算法的SLAM问题分析[J].城市建筑. 2020,17(11)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
边栏推荐
- R language uses image of magick package_ Mosaic functions and images_ The flatten function stacks multiple pictures together to form a stack layers on top of each other
- Activity生命周期
- 千人規模互聯網公司研發效能成功之路
- Talk about SOC startup (x) kernel startup pilot knowledge
- 【最短路】Acwing1128信使:floyd最短路
- Vuthink正确安装过程
- Using ENSP to do MPLS pseudo wire test
- 一起探索云服务之云数据库
- 【问道】编译原理
- 【系统设计】指标监控和告警系统
猜你喜欢

自动化测试框架
The Oracle message permission under the local Navicat connection liunx is insufficient

本地navicat连接liunx下的oracle报权限不足

高考作文,高频提及科技那些事儿……

對比學習之 Unsupervised Learning of Visual Features by Contrasting Cluster Assignments
数据库同步工具 DBSync 新增对MongoDB、ES的支持
Solve the problem that vscode can only open two tabs
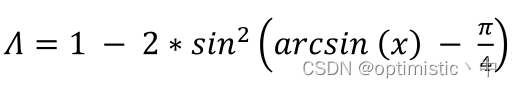
关于SIoU《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan 》的一些看法及代码实现
测试优惠券要怎么写测试用例?

Unsupervised learning of visual features by contracting cluster assignments
随机推荐
Internet Protocol
Audit migration
Various uses of vim are very practical. I learned and summarized them in my work
. Net Maui performance improvement
0.96 inch IIC LCD driver based on stc8g1k08
Electron adding SQLite database
Verilog realizes nixie tube display driver [with source code]
【最短路】ACwing 1127. 香甜的黄油(堆优化的dijsktra或spfa)
The Oracle message permission under the local Navicat connection liunx is insufficient
Learning notes | data Xiaobai uses dataease to make a large data screen
Unsupervised learning of visual features by contracting cluster assignments
Enclosed please find. Net Maui's latest learning resources
正在运行的Kubernetes集群想要调整Pod的网段地址
【时间格式工具函数的封装】
简单介绍一下闭包及它的一些应用场景
一度辍学的数学差生,获得今年菲尔兹奖
软件设计之——“高内聚低耦合”
Two week selection of tdengine community issues | phase II
禁锢自己的因素,原来有这么多
Case study of Jinshan API translation function based on retrofit framework