当前位置:网站首页>[opencv] [image gradient]
[opencv] [image gradient]
2022-07-02 12:52:00 【A sea of stars】
Let's calculate the gradient of each pixel in the image
We can use first-order Sobel Operator and Scharr operator , And use secondary Laplace operator , The experiment is as follows :
The original image is :
The gradient of the first-order operator is calculated as follows :
Find the gradient of each pixel of the image . Calculated above sobel The operator can be approximated as X and Y Directional gradient , So the total gradient is :
G = (Gx^2 + Gy ^2) ^ 0.5 Or it can be approximately calculated as
G = |Gx| + |Gy|
Second order operator , The gradient can be obtained directly .
import numpy as np
import random
import cv2
import matplotlib.pyplot as plt
# Show the image , Encapsulate as a function
def cv_show_image(name, img):
cv2.imshow(name, img)
cv2.waitKey(0) # Waiting time , In milliseconds ,0 Represents any key termination
cv2.destroyAllWindows()
img = cv2.imread('images/yuan.png') # Read the original image
print(img.shape)
# Sobel operator , For example, the gradient in the right direction
# [[-1, 0, 1],
# Gx = [-2, 0, 2],
# [-1, 0, 1]]
# For example, it is a downward gradient
# [[-1, -2, -1],
# Gy = [0, 0, 0],
# [1, 2, 1]]
# It is equivalent to subtracting the pixel value on the left from the pixel value on the right
# dst = cv2.Sobel(src, ddepth, dx, dy, ksize)
# src: Input the original image
# ddepth: The depth of the image , It's usually -1
# dx and dy: Horizontal and vertical
# ksize: The size of the convolution kernel
# Let's look at the results of operations in different directions
# The result of pixel subtraction is positive and negative , If there is a negative number ,opencv The default truncation is 0
# But what we want to see is the size of the difference , Even negative numbers have different values , Cannot be smeared 0 No difference , So we need to save negative numbers , Negative calculation results can be retained .
sobel_x = cv2.Sobel(img, cv2.CV_64F, 1, 0, 3) # The image is converted to a form with a negative number , Because the number of digits is higher .
sobel_x_abs = cv2.convertScaleAbs(sobel_x) # Take the absolute value , Keep our difference value
sobel_y = cv2.Sobel(img, cv2.CV_64F, 0 ,1, 3) # The image is converted to a form with a negative number , Because the number of digits is higher .
sobel_y_abs = cv2.convertScaleAbs(sobel_y) # Take the absolute value , Keep our difference value
# Find the gradient of each pixel of the image . Calculated above sobel The operator can be approximated as X and Y Directional gradient , So the total gradient is :
# G = (Gx^2 + Gy^2)^0.5 Or it can be approximately calculated as
# G = |Gx| + |Gy|
sobel_xy_add = cv2.addWeighted(sobel_x_abs, 0.5, sobel_y_abs, 0.5, 0) # Use x + y To find the gradient .
sobel_xy_abs_add = cv2.convertScaleAbs(sobel_xy_add) # Take the absolute value , Keep our difference value
# The following method is not recommended , This effect is not very good .
sobel_xy = cv2.Sobel(img, cv2.CV_64F, 1, 1, 3) # The image is converted to a form with a negative number , Because the number of digits is higher .
sobel_xy_abs = cv2.convertScaleAbs(sobel_xy) # Take the absolute value , Keep our difference value
ret = np.hstack((sobel_x, sobel_y, sobel_xy_add, sobel_xy))
cv2.imshow('sobel_src', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()
ret = np.hstack((sobel_x_abs, sobel_y_abs, sobel_xy_abs_add, sobel_xy_abs))
cv2.imshow('sobel_abs', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()
# Two other operators for finding image gradient , This and Sobel Operators are very similar , Or the degree of emphasis is different
# Scharr operator
# [[-3, 0, 3],
# Gx = [-10, 0, 10],
# [-3, 0, 3]]
# For example, it is a downward gradient
# [[-3, -10, -3],
# Gy = [0, 0, 0],
# [3, 10, 3]]
# Let's look at the results of operations in different directions
# The result of pixel subtraction is positive and negative , If there is a negative number ,opencv The default truncation is 0
# But what we want to see is the size of the difference , Even negative numbers have different values , Cannot be smeared 0 No difference , So we need to save negative numbers , Negative calculation results can be retained .
scharr_x = cv2.Scharr(img, cv2.CV_64F, 1, 0, 3) # The image is converted to a form with a negative number , Because the number of digits is higher .
scharr_x_abs = cv2.convertScaleAbs(scharr_x) # Take the absolute value , Keep our difference value
scharr_y = cv2.Scharr(img, cv2.CV_64F, 0 ,1, 3) # The image is converted to a form with a negative number , Because the number of digits is higher .
scharr_y_abs = cv2.convertScaleAbs(scharr_y) # Take the absolute value , Keep our difference value
# Find the gradient of each pixel of the image . Calculated above sobel The operator can be approximated as X and Y Directional gradient , So the total gradient is :
# G = (Gx^2 + Gy^2)^0.5 Or it can be approximately calculated as
# G = |Gx| + |Gy|
scharr_xy_add = cv2.addWeighted(scharr_x_abs, 0.5, scharr_y_abs, 0.5, 0) # Use x + y To find the gradient .
scharr_xy_abs_add = cv2.convertScaleAbs(scharr_xy_add) # Take the absolute value , Keep our difference value
ret = np.hstack((scharr_x, scharr_y, scharr_xy_add))
cv2.imshow('scharr_src', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()
ret = np.hstack((scharr_x_abs, scharr_y_abs, scharr_xy_abs_add))
cv2.imshow('scharr_abs', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()
# Laplace operator
# Laplace The operator can approximately calculate the second derivative of the image , It has rotation invariance , That is, edges in all directions can be detected .
# Laplace There are two kinds of operators , Consider separately 4- Adjacency (D4) and 8- Adjacency (D8) Second order differential of two neighborhoods .
# For example, one 3x3 Of 4- Adjacency is
# for example 4- Adjacency
# [[0, -1, 0],
# [-1, 4, -1],
# [ 0, -1, 0]]
# for example 8- Adjacency
# [[-1, -1, -1],
# [ -1, 8, -1],
# [ -1, -1, -1]]
Laplacian = cv2.Laplacian(img, cv2.CV_64F) # Because it is second-order , No, x and y The concept of direction
Laplacian_abs = cv2.convertScaleAbs(Laplacian) # Take the absolute value , Keep our difference value
cv_show_image('Laplacian', Laplacian)
# Finally, summarize the effects of the three methods
ret = np.hstack((sobel_xy_abs_add, scharr_xy_abs_add, Laplacian_abs))
cv2.imshow('all_here', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()
The effect is as follows :
Use Sobel operator , The effect of not adding absolute value operation :
Use Sobel operator , Add the effect of absolute value operation :
Use Scharr operator , The effect of not adding absolute value operation :
Use Scharr operator , Add the effect of absolute value operation :
Use Laplace operator , The effect of adding absolute value and not adding absolute value 
Finally, add the absolute value to each xy Summary of directions , The effect is as follows :

The overall effect shows , The effect of using second-order operators is better .
边栏推荐
- Mongodb redis differences
- JSON序列化 与 解析
- 阿里发布的Redis开发文档,涵盖了所有的redis操作
- Docsify deploy IIS
- Linear DP acwing 896 Longest ascending subsequence II
- The redis development document released by Alibaba covers all redis operations
- Js3day (array operation, JS bubble sort, function, debug window, scope and scope chain, anonymous function, object, Math object)
- . Net, C # basic knowledge
- Linear DP acwing 899 Edit distance
- [ybtoj advanced training guidance] judgment overflow [error]
猜你喜欢

Js2day (also i++ and ++i, if statements, ternary operators, switch, while statements, for loop statements)
LTC3307AHV 符合EMI标准,降压转换器 QCA7005-AL33 PHY

Linear DP acwing 896 Longest ascending subsequence II
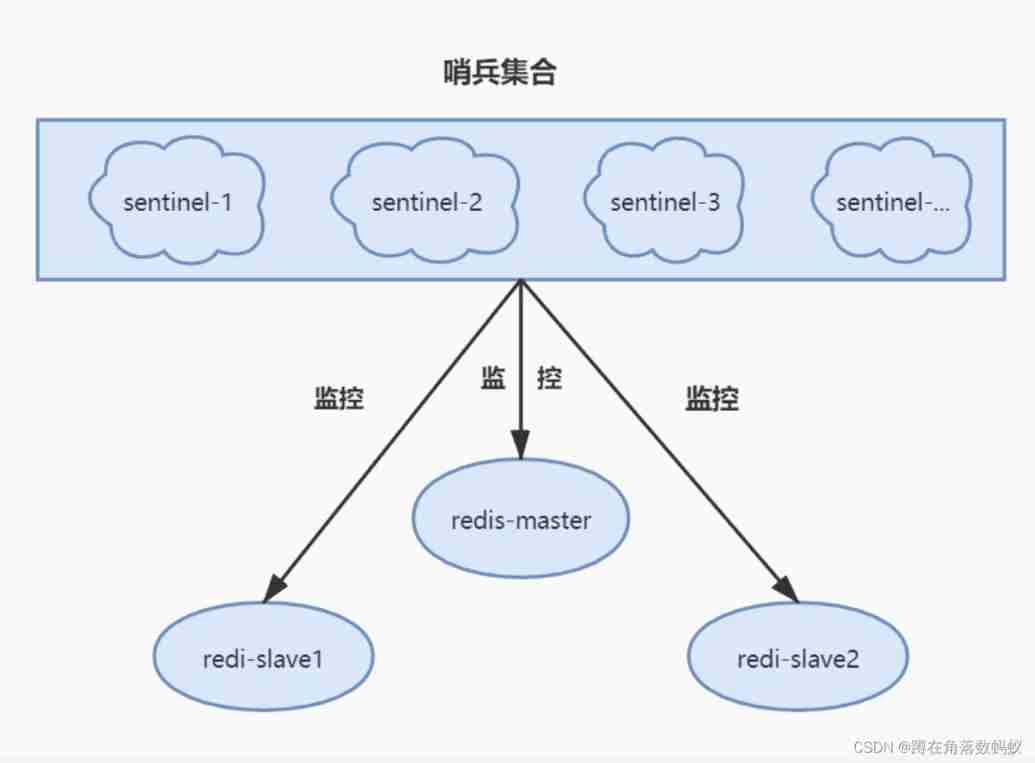
Redis sentinel mechanism and configuration

js3day(数组操作,js冒泡排序,函数,调试窗口,作用域及作用域链,匿名函数,对象,Math对象)

Heap acwing 838 Heap sort

JS7day(事件对象,事件流,事件捕获和冒泡,阻止事件流动,事件委托,学生信息表案例)

js5day(事件监听,函数赋值给变量,回调函数,环境对象this,全选反选案例,tab栏案例)
线性DP AcWing 897. 最长公共子序列

移动式布局(流式布局)
随机推荐
ASP. Net MVC default configuration, if any, jumps to the corresponding program in the specified area
Some sudden program ideas (modular processing)
堆 AcWing 839. 模拟堆
Lekao.com: experience sharing of junior economists and previous candidates in customs clearance
Package management tools
线性DP AcWing 902. 最短编辑距离
async/await 异步函数
8A Synchronous Step-Down regulator tps568230rjer_ Specification information
Deep Copy Event bus
js1day(輸入輸出語法,數據類型,數據類型轉換,var和let區別)
染色法判定二分图 AcWing 860. 染色法判定二分图
Wechat official account payment prompt MCH_ ID parameter format error
Openssh remote enumeration username vulnerability (cve-2018-15473)
Js1day (input / output syntax, data type, data type conversion, VaR and let differences)
Dijkstra AcWing 850. Dijkstra求最短路 II
BOM DOM
Floyd AcWing 854. Floyd finds the shortest path
Dijkstra AcWing 850. Dijkstra finding the shortest circuit II
Js8day (rolling event (scroll family), offset family, client family, carousel map case (to be done))
Js6day (search, add and delete DOM nodes. Instantiation time, timestamp, timestamp cases, redrawing and reflow)