当前位置:网站首页>Summary of regularization methods
Summary of regularization methods
2022-07-05 01:36:00 【Xiaobai learns vision】
Read the directory
- LP norm
- L1 norm
- L2 norm
- L1 Norm sum L2 The difference of norm
- Dropout
- Batch Normalization
- normalization 、 Standardization & Regularization
- Reference
In summary, regularization (Regularization) Before , Let's talk about what regularization is first , Why regularize .
I think regularization is a bit too abstract and broad , In fact, the essence of regularization is very simple , It is a means or operation to restrict or restrict a problem a priori in order to achieve a specific purpose . The purpose of using regularization in the algorithm is to prevent over fitting of the model . When it comes to regularization , Many students may immediately think of the commonly used L1 Norm sum L2 norm , Before summarizing , Let's take a look first LP What the hell is the norm .
LP norm
Norm is simple and can be understood as representing distance in vector space , And the definition of distance is very abstract , As long as it's not negative 、 introspect 、 Trigonometric inequality can be called distance .
LP Norm is not a norm , It's a set of norms , Its definition is as follows :
p The range is
.p stay (0,1) It's not the norm defined in the scope , Because it violates the trigonometric inequality .
according to p The change of , The norm also has different changes , Borrow a classic about P The change of norm is shown as follows :
The figure above shows p from 0 When it comes to positive infinity , Unit ball (unit ball) The change of . stay P The unit ball defined by norm is convex set , But when 0<p<1 when , The unit sphere under this definition is not a convex set ( We mentioned this before , When 0<p<1 Time is not a norm ).
That's the question ,L0 What is a norm ?
L0 Norm is the number of non-zero elements in a vector , The formula is as follows :
We can minimize L0 norm , To find the least optimal sparse features . But unfortunately ,L0 The optimization problem of norm is a NP hard problem (L0 Norms are also nonconvex ). therefore , In practical application, we often pay attention to L0 Convex relaxation , There is a theoretical proof ,L1 Norm is L0 Optimal convex approximation of norm , So we usually use L1 Norm instead of direct optimization L0 norm .
L1 norm
according to LP We can easily get the definition of norm L1 The mathematical form of norm :
It can be seen from the above formula that ,L1 Norm is the sum of the absolute values of the elements of a vector , Also known as " Sparse regular operators "(Lasso regularization). So here comes the question , Why do we want to be sparse ? Sparseness has many advantages , The most direct two :
- feature selection
- Interpretability
L2 norm
L2 Norm is the most familiar , It's Euclidean distance , The formula is as follows :
L2 Norms have many names , Some people call its return “ Ridge return ”(Ridge Regression), It's also called “ Weight attenuation ”(Weight Decay). With L2 The dense solution can be obtained by taking norm as regular term , That is, the parameters corresponding to each feature w Very small , Close to the 0 But not for 0; Besides ,L2 Norm as regularization term , It can prevent the model from being too complex to fit the training set , So as to improve the generalization ability of the model .
L1 Norm sum L2 The difference of norm
introduce PRML A classic diagram to illustrate L1 and L2 The difference of norm , As shown in the figure below :
As shown in the figure above , The blue circle indicates the possible solution range of the problem , Orange denotes the possible solution range of the regular term . And the whole objective function ( The original question + The regularization ) There are solutions if and only if the ranges of two solutions are tangent . It's easy to see from the picture above , because L2 The range of norm solution is circle , So the point of tangency is very likely not on the axis , And because the L1 The norm is a diamond ( The vertex is convex ), The point of tangency is more likely to be on the axis , And the point on the axis has one characteristic , Only one coordinate component is not zero , Other coordinate components are zero , It's sparse . So here's the conclusion ,L1 Norms can lead to sparse solutions ,L2 Norm leads to dense solution .
From the perspective of Bayesian priors , When training a model , It's not enough to rely on the current training data set , In order to achieve better generalization ability , It is often necessary to add a priori term , Adding a regular term is equivalent to adding a priori .
- L1 The norm is equivalent to adding a Laplacean transcendental ;
- L2 The norm is equivalent to adding a Gaussian transcendental .
More detailed L1 Norm sum L2 Norm difference , Please click on 《 More detailed L1 and L2 Regularization interpretation 》.
As shown in the figure below :
Dropout
Dropout It is a regularization method often used in deep learning . Its practice can be simply understood as in DNNs In the process of training with probability p Discard some neurons , Even if the output of the discarded neurons is 0.Dropout The following figure can be instantiated :
We can understand it intuitively from two aspects Dropout The regularization effect of :
- stay Dropout In each round of training, the operation of randomly losing neurons is equivalent to many DNNs Take the average , Therefore, it has vote The effect of .
- Reduce complex co adaptation between neurons . When the hidden layer neurons are randomly deleted , It makes the fully connected network have a certain degree of sparseness , So as to effectively reduce the synergistic effect of different characteristics . in other words , Some features may depend on the interaction of hidden nodes of fixed relationships , And by Dropout Words , It effectively organizes the situation where some features have effect only in the presence of other features , The robustness of neural network is increased .
Batch Normalization
Batch normalization (Batch Normalization) Strictly speaking, it belongs to normalization means , Mainly used to accelerate the convergence of the network , But it also has a certain degree of regularization effect .
Here is a reference to Dr. Wei Xiushen's Zhihu answer covariate shift The explanation of .
Note: the following is quoted from Dr. Wei Xiushen's reply :
As we all know, a classical hypothesis in statistical machine learning is “ Source space (source domain) And target space (target domain) Data distribution of (distribution) It's consistent ”. If it's not consistent , So there are new machine learning problems , Such as transfer learning/domain adaptation etc. . and covariate shift It's a branch problem under the hypothesis of inconsistent distribution , It means that the conditional probabilities of source space and target space are the same , But the marginal probability is different . If you think about it, you will find , You bet , For each layer output of neural network , Because they are operated in layers , The distribution is obviously different from the input signal distribution of each layer , And the difference will increase with the depth of the network , But what they can “ instructions ” Sample label of (label) It's still the same , This is in line with covariate shift The definition of .
BN In fact, the basic idea of is quite intuitive , Because the active input value of neural network before nonlinear transformation (X = WU + B,U It's input ), As the network deepens , Its distribution is gradually shifted or changed ( That is to say covariate shift). The reason why training convergence is slow , Generally, the whole distribution is gradually close to the upper and lower limits of the value range of the nonlinear function ( about Sigmoid In terms of functions , Means activate the input value (X = WU + B) Are large negative and positive values . So this causes the gradient of the lower layer neural network to disappear when it propagates backward , This is the essential reason why the convergence of deep neural network is getting slower and slower . and BN It is through certain standardized means , Force the distribution of the input value of any neuron in each layer of neural network back to the mean value 0 The variance of 1 The standard normal distribution of , Avoid the gradient dispersion problem caused by the activation function . So it's not so much BN The effect of the treatment is to alleviate covariate shift, Might as well say BN It can alleviate the problem of gradient dispersion .
normalization 、 Standardization 、 Regularization
Regularization we have mentioned , Here is a brief introduction to normalization and standardization .
normalization (Normalization): The goal of normalization is to find some kind of mapping relationship , Map the raw data to [a,b] On interval . commonly a,b Will take [-1,1],[0,1] These combinations .
There are generally two application scenarios :
- Change the number into (0, 1) Decimal between
- Convert a dimensional number into a dimensionless number
Commonly used min-max normalization:
Standardization (Standardization): Use the large number theorem to transform the data into a standard normal distribution , The standardized formula is :
The difference between normalization and Standardization :
We can explain this simply :
What is the normalized scaling “ Beat flat ” Unified to the interval ( Only by the extreme value ), And standardized scaling is more “ elastic ” and “ dynamic ” Of , It has a lot to do with the distribution of the whole sample .
It is worth noting that :
normalization : Zoom is just the same as the maximum 、 It's about the difference in the minimum .
Standardization : Scaling has something to do with every point , Through variance (variance) reflected . Compared with normalization , All data points in standardization contribute ( Through mean and standard deviation ).
Why standardization and normalization ?
- Improve model accuracy : After normalization , The characteristics of different dimensions are numerically comparable , Can greatly improve the accuracy of the classifier .
- Accelerate model convergence : After standardization , The optimization process of the optimal solution will obviously become smooth , It's easier to converge to the optimal solution correctly . As shown in the figure below :
Reference
1. Andrew Ng In depth learning course
2. Must Know Tips/Tricks in Deep Neural Networks (by Xiu-Shen Wei)
边栏推荐
- 【CTF】AWDP总结(Web)
- Hand drawn video website
- [Chongqing Guangdong education] National Open University spring 2019 1042 international economic law reference questions
- [pure tone hearing test] pure tone hearing test system based on MATLAB
- node工程中package.json文件作用是什么?里面的^尖括号和~波浪号是什么意思?
- 微信小程序;胡言乱语生成器
- How to use words to describe breaking change in Spartacus UI of SAP e-commerce cloud
- PowerShell: use PowerShell behind the proxy server
- Global and Chinese markets for industrial X-ray testing equipment 2022-2028: Research Report on technology, participants, trends, market size and share
- Win: add general users to the local admins group
猜你喜欢
Wechat applet: independent background with distribution function, Yuelao office blind box for making friends
![[wave modeling 3] three dimensional random real wave modeling and wave generator modeling matlab simulation](/img/22/6d3867015811aae29b8a7df5ee3d0b.png)
[wave modeling 3] three dimensional random real wave modeling and wave generator modeling matlab simulation
增量备份 ?db full

Yyds dry inventory swagger positioning problem ⽅ formula
Wechat applet: new independent backstage Yuelao office one yuan dating blind box
DOM basic syntax
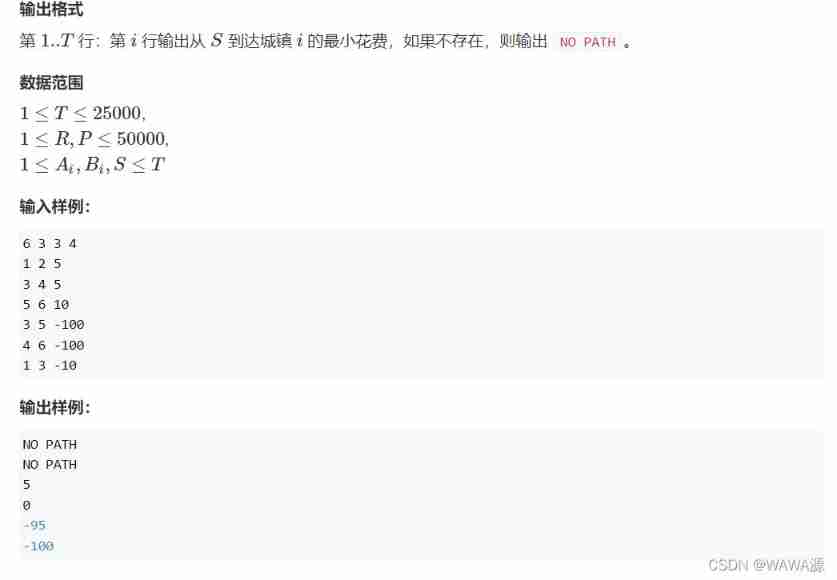
Roads and routes -- dfs+topsort+dijkstra+ mapping
![[development of large e-commerce projects] performance pressure test - Optimization - impact of middleware on performance -40](/img/e4/0bdee782a65028b2bc87db85d48738.png)
[development of large e-commerce projects] performance pressure test - Optimization - impact of middleware on performance -40
Basic operation of database and table ----- phased test II
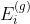
MATLB|多微电网及分布式能源交易
随机推荐
Are you still writing the TS type code
Nebula Importer 数据导入实践
Win: use PowerShell to check the strength of wireless signal
Basic operation of database and table ----- the concept of index
微信小程序:独立后台带分销功能月老办事处交友盲盒
"2022" is a must know web security interview question for job hopping
Global and Chinese market of nutrient analyzer 2022-2028: Research Report on technology, participants, trends, market size and share
Exploration and practice of integration of streaming and wholesale in jd.com
PHP 基础篇 - PHP 中 DES 加解密详解
phpstrom设置函数注释说明
Yyds dry inventory swagger positioning problem ⽅ formula
Discrete mathematics: reasoning rules
微信小程序:微群人脉微信小程序源码下载全新社群系统优化版支持代理会员系统功能超高收益
Outlook:总是提示输入用户密码
Wechat applet: independent background with distribution function, Yuelao office blind box for making friends
MySQL REGEXP:正则表达式查询
LeetCode周赛 + AcWing周赛(T4/T3)分析对比
Introduction to the gtid mode of MySQL master-slave replication
Mysql database | build master-slave instances of mysql-8.0 or above based on docker
Five ways to query MySQL field comments!