当前位置:网站首页>Visual explanation of Newton iteration method
Visual explanation of Newton iteration method
2022-07-05 00:29:00 【deephub】
Newton's iteration (Newton’s method) Also known as Newton - Ralph ( Raffson ) Method (Newton-Raphson method), It's Newton in 17 An approximate method for solving equations in real and complex fields was proposed in the 20th century .
With Isaac Newton and Joseph Raphson Named Newton-Raphson The method is designed as a root algorithm , This means that its goal is to find the function f(x)=0 Value x. Geometrically, it can be regarded as x Value , At this time, the function and x Axis intersection .
Newton-Raphson Algorithms can also be used for simple things , For example, given the previous continuous evaluation results , Finding out the prediction needs to be obtained in the final exam A The scores of . In fact, if you've ever been Microsoft Excel Solver functions have been used in , Then I used something like Newton-Raphson Such a rooting Algorithm . Another complex use case is to use Black-Scholes The formula reversely solves the implied volatility of financial option contracts .
Newton-Raphson The formula
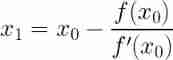
Although the formula itself is very simple , But if you want to know what it is actually doing, you need to look carefully .
First , Let's review the overall approach :
1、 Preliminary guess where the root may be
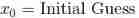
2、 application Newton-Raphson The formula gets the updated guess , This guess will be closer to the root than the initial guess
3、 Repeat step 2, Until the new guess is close enough to the real value .
Is that enough ?Newton-Raphson Method gives the approximate value of the root , Although it is usually close enough for any reasonable application ! But how do we define close enough ? When to stop iteration ?
In general Newton-Raphson Method there are two ways to deal with when to stop .1、 If you guess that the change from one step to the next does not exceed the threshold , for example 0.00001, Then the algorithm will stop and confirm that the latest guess is close enough .2、 If we reach a certain number of guesses but still do not reach the threshold , Then we'll give up and continue to guess .
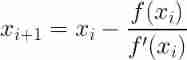
From the formula we can see , Every new guess is that our previous guess has been adjusted by a mysterious number . If we visualize this process through an example , It will soon know what happened !
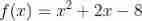
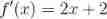
As an example , Let's consider the above function , And make one x=10 Initial guess ( Notice that the actual root here is x=4). Newton-Raphson The first few guesses of the algorithm are in the following GIF Medium visualization

Our initial guess was x=10. In order to calculate our next guess , We need to evaluate the function itself and its application in x=10 Derivative at . stay 10 The derivative of the function evaluated at simply gives the slope of the tangent curve at that point . The tangent is at GIF Drawn as Tangent 0.
Look at the position of the next guess relative to the previous tangent , Did you notice anything ? The next guess appears between the previous tangent and x Where the axes intersect . This is it. Newton-Raphson Highlights of the method !

in fact , f(x)/f’(x) It just gives our current guess and tangent crossing x The distance between the points of the axis ( stay x In the direction of ). It is this distance that tells us the guess of each update , As we are GIF As seen in , As we approach the root itself , Updates are getting smaller and smaller .

What if the function cannot be differentiated manually ?
The above example is a function that can be easily differentiated by hand , This means that we can calculate without difficulty f’(x). However , This may not be the case , And there are some useful techniques that can approximate the derivative without knowing its analytical solution .
These derivative approximation methods are beyond the scope of this paper , You can find more information about finite difference methods .
problem
Keen readers may have found a problem from the above example , Even if our example function has two roots (x=-2 and x=4),Newton-Raphson Methods can only recognize one root . Newton iteration will converge to a certain value according to the selection of initial value , So we can only find a value . If you need other values , It is to bring in the root of the current solution and reduce the equation to order , Then find the second root . This is, of course, a problem , Is not the only drawback of this approach :
- Newton's method is an iterative algorithm , Every step needs to solve the objective function Hessian The inverse of the matrix , The calculation is complicated .
- The convergence rate of Newton's method is second order , For a positive definite quadratic function, the optimal solution can be obtained by one-step iteration .
- Newton's method is locally convergent , When the initial point is not selected , Often leads to non convergence ;
- Second order Hessian The matrix must be reversible , Otherwise, the algorithm is difficult .
Comparison with gradient descent method
Gradient descent method and Newton method are both iterative solutions , But the gradient descent method is a gradient solution , And Newton's method / The quasi Newton method uses second order Hessian The inverse matrix or pseudo inverse matrix of a matrix is solved . In essence , Newton's method is second order convergence , Gradient descent is first order convergence , So Newton's method is faster . In a more popular way , For example, you want to find the shortest path to the bottom of a basin , The gradient descent method only takes one step at a time from your current position in the direction with the largest slope , Newton's method in choosing direction , It's not just about whether the slope is big enough , And think about it when you take a step , Is the slope going to get bigger . It can be said that Newton's method looks a little further than gradient descent method , To get to the bottom faster .( Newton's method has a longer view , So avoid detours ; Relatively speaking , The gradient descent method only considers the local optimum , No overall thinking ).
Then why not use Newton's method instead of gradient descent ?
- Newton's method uses the second derivative of the objective function , In the case of high dimensions, this matrix is very large , Computing and storage are problems .
- In the case of small quantities , The estimation noise of Newton method for the second derivative is too large .
- When the objective function is nonconvex , Newton method is easily attracted by saddle point or maximum point
In fact, there is no good theoretical guarantee for the convergence of the current deep neural network algorithm , Deep neural network is only used because it has better effect in practical application , But can the gradient descent method converge on the deep neural network , Whether it converges to the global best is still uncertain . And the second-order method can obtain higher accuracy solutions , But when the accuracy of neural network parameters is not high, it becomes a problem , Under the deep model, if the parameter accuracy is too high , The generalization of the model will be reduced , Instead, it will increase the risk of model over fitting .
https://www.overfit.cn/post/37cdf43c67df46bbb1ac52418a4237ef
author :Rian Dolphin
边栏推荐
- Application of multi loop instrument in base station "switching to direct"
- Distributed base theory
- TS快速入门-函数
- Power operation and maintenance cloud platform: open the new mode of "unattended and few people on duty" of power system
- 人生无常,大肠包小肠, 这次真的可以回家看媳妇去了。。。
- Date time type and format in MySQL
- 公司要上监控,Zabbix 和 Prometheus 怎么选?这么选准没错!
- [Peking University] tensorflow2.0-1-opening
- P4281 [AHOI2008]紧急集合 / 聚会(LCA)
- Oracle case: SMON rollback exception causes instance crash
猜你喜欢
Continuous modification of business scenario functions
lambda表达式

npm install报错 强制安装

IELTS examination process, what to pay attention to and how to review?
Ap8022 switching power supply small household appliances ACDC chip offline switching power supply IC
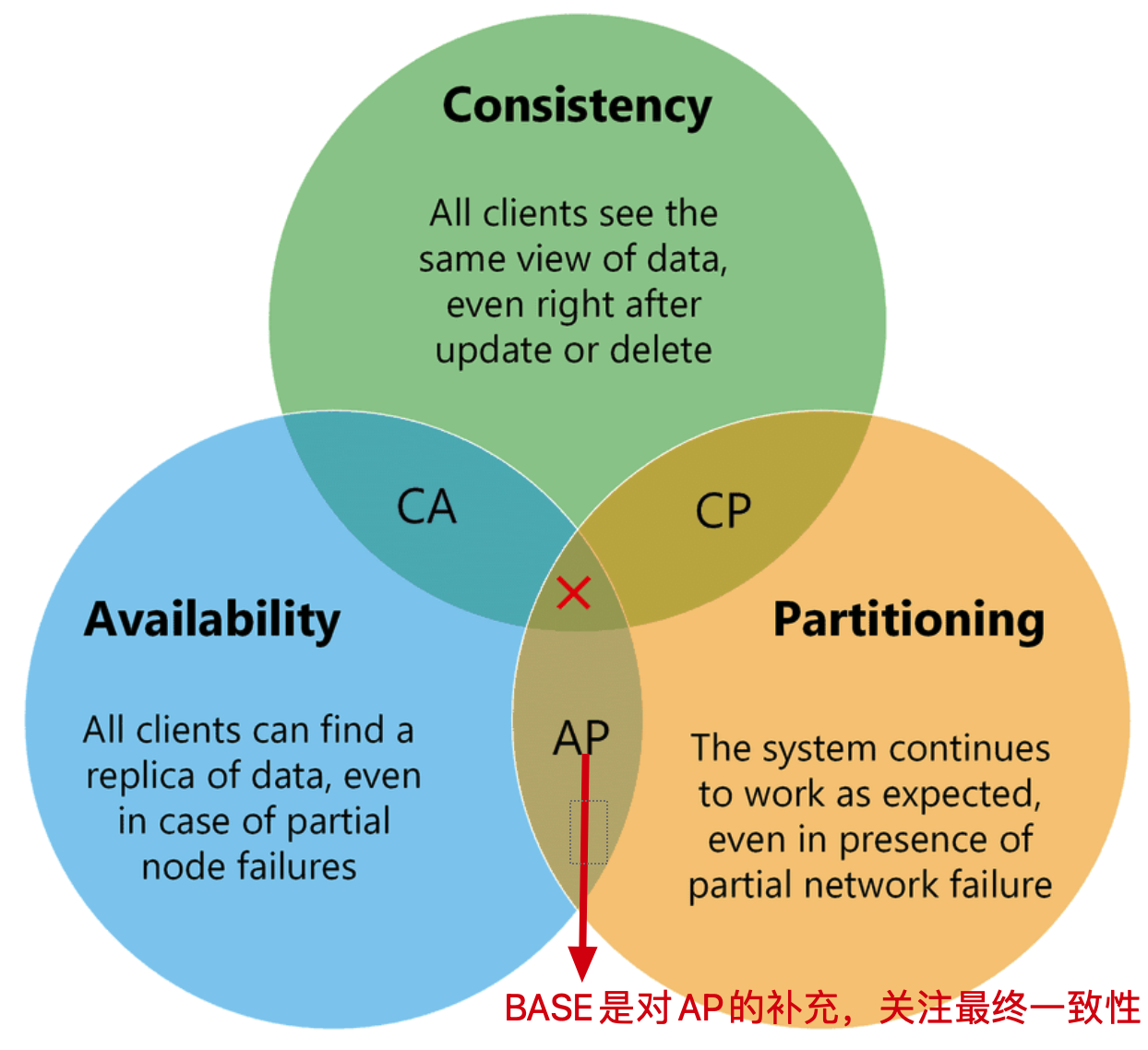
分布式BASE理论
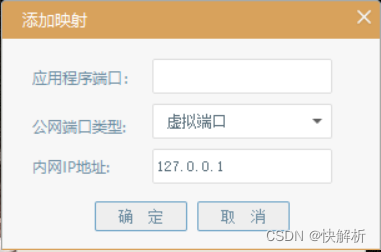
How to use fast parsing to make IOT cloud platform

How to do the project of computer remote company in foreign Internet?
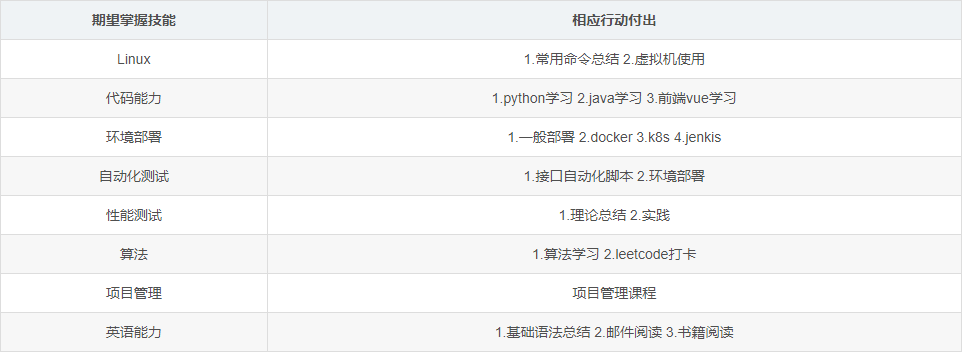
What did I pay for it transfer to testing post from confusion to firmness?

业务场景功能的继续修改
随机推荐
IELTS examination process, what to pay attention to and how to review?
业务实现-日志写到同一个行数据里面
MySQL uses the explain tool to view the execution plan
abc 258 G - Triangle(bitset)
Daily practice (18): stack containing min function
[论文阅读] TUN-Det: A Novel Network for Thyroid Ultrasound Nodule Detection
2022.07.03(LC_6109_知道秘密的人数)
Tester's algorithm interview question - find mode
Complete knapsack problem (template)
基本放大电路的学习
Design of emergency lighting evacuation indication system for urban rail transit station
Fast parsing intranet penetration helps enterprises quickly achieve collaborative office
Nine Qi single chip microcomputer ny8b062d single key control four LED States
leetcode518,377
The waterfall flow layout demo2 (method 2) used by the uniapp wechat applet (copy and paste can be used without other processing)
const、volatile和restrict的作用和用法总结
[selenium automation] common notes
1189. Maximum number of "balloons"
P4281 [ahoi2008] emergency assembly / gathering (LCA)
Multilingual Wikipedia website source code development part II