当前位置:网站首页>[dynamic planning hundred questions strengthening plan] 11~20 (continuously updating)
[dynamic planning hundred questions strengthening plan] 11~20 (continuously updating)
2022-07-27 04:38:00 【Xiao Yu, colicsin】
Strengthen in summer DP A plan for learning , Brush some every day cf, Every day, it surpasses the living gods (bushi)
The questions are cf The inside has dp Labeled , There are also some simple problems such as greed
11.CF_1677A(1600)
Click here directly
tag -> brute force , dp , math
label : Violence optimization , Preprocessing , Prefixes and suffixes
The main idea of the topic :
Now let's give you a length of n Permutation p, Respectively p1,p2,p3… also pi≠pj(i≠j) Ask how many combinations there can be [a,b,c,d] Satisfy (a<b<c<d) also ( p a < p c p_a<p_c pa<pc and p b > p d p_b>p_d pb>pd)
Ideas :
Follow the usual line of thinking , The most violent solution is that the time complexity is O(n4) Enumeration , Now let's think about how to optimize .
You can handle prefixes and suffixes , Fix b and c, Then for each group (b,c) The answer is b Left side less than a[c] The number of and c The right side is smaller than a[b] The product of the number of
The preprocessing code is as follows :
for(int i=1;i<=n;i++)
v[i]=0;
for(int i=1;i<=n;i++)
{
int s=0;
for(int j=1;j<=n;j++)
{
f1[i][j]=s;
s+=v[j];
}
v[a[i]]=1;
}
for(int i=1;i<=n;i++)
v[i]=0;
for(int i=n;i>=1;i--)
{
int s=0;
for(int j=1;j<=n;j++)
{
f2[i][j]=s;
s+=v[j];
}
v[a[i]]=1;
}
Finally, accumulate the result , Pay attention long long
12.CF_1661B(1300)
Click here directly
tag -> mitmasks , brute force , dp , dfs and similar ,greedy
label : greedy , An operation
The main idea of the topic :
Now give me a number v, It can be executed in one operation :
1. send $ v=(v+1) mod 32768$
2. send v = ( 2 ∗ v ) m o d 32768 v=(2*v)mod32768 v=(2∗v)mod32768
Now you have n A digital , Ask how many times you need to operate each number at least to make it become 0?
Ideas :
32768, A very sensitive number ,32768 It happens to be 2^15, in other words , No matter what the numbers are , Can be in 15 operations 2 Then make it 0, Therefore, the minimum operand cannot be greater than 15.
Because of the operation 2 Every time I take 2, We can look at it from a binary point of view , multiply 2 Just add one at the back 0, and 215 Namely 1000000000000000(15 individual 0), Then for operation 1, You can only make the end of its binary number +1, But operation 1 For continuous 1 Come on , Contribution ratio operation 2 Big , such as 100111111 Want to be 128 Multiple , It only needs +1 become 1010000000, And if you use operations 2, You need to add 7 individual 0, Perform seven operations 2.
So our greedy strategy is obvious : Enumerate the addition and multiplication operations respectively , Get the minimum value of the target result
Core code :
int get_cal(int x)
{
int pos=15;
for(int i=0;i<=15;i++)
{
if(x&(1<<i))// Judge x After i Isn't it 1
{
pos=i;
break;
}
}
return 15-pos;
}
int solve(int n)
{
int ans=1e7;
for(int j=0;j<=15;j++)
{
ans=min(ans,j+get_cal((n+j)%MOD));
}
return ans;
}
With the 2 Multiple of , Keep a sensitive heart , Is to consider whether bit operation bitmasks Easier to solve
边栏推荐
- C get UUID
- 利用JSON类型在mysql中实现数组功能
- ELS square display principle
- [machine learning network] BP neural network and deep learning-6 deep neural networks (DNN)
- Effect Hook
- 可视化领域 SVG
- 【动态规划百题强化计划】11~20(持续更新中)
- RSA asymmetric encryption and decryption signature verification tool
- Okaleido ecological core equity Oka, all in fusion mining mode
- Spark practice case (upgraded version)
猜你喜欢

Is the e-commerce billing system important? How should the platform choose billing service providers?

Influxdb basic understanding
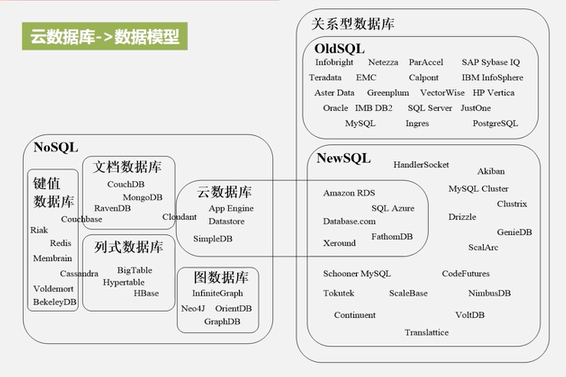
第六章:云数据库

Yolov4网络详解
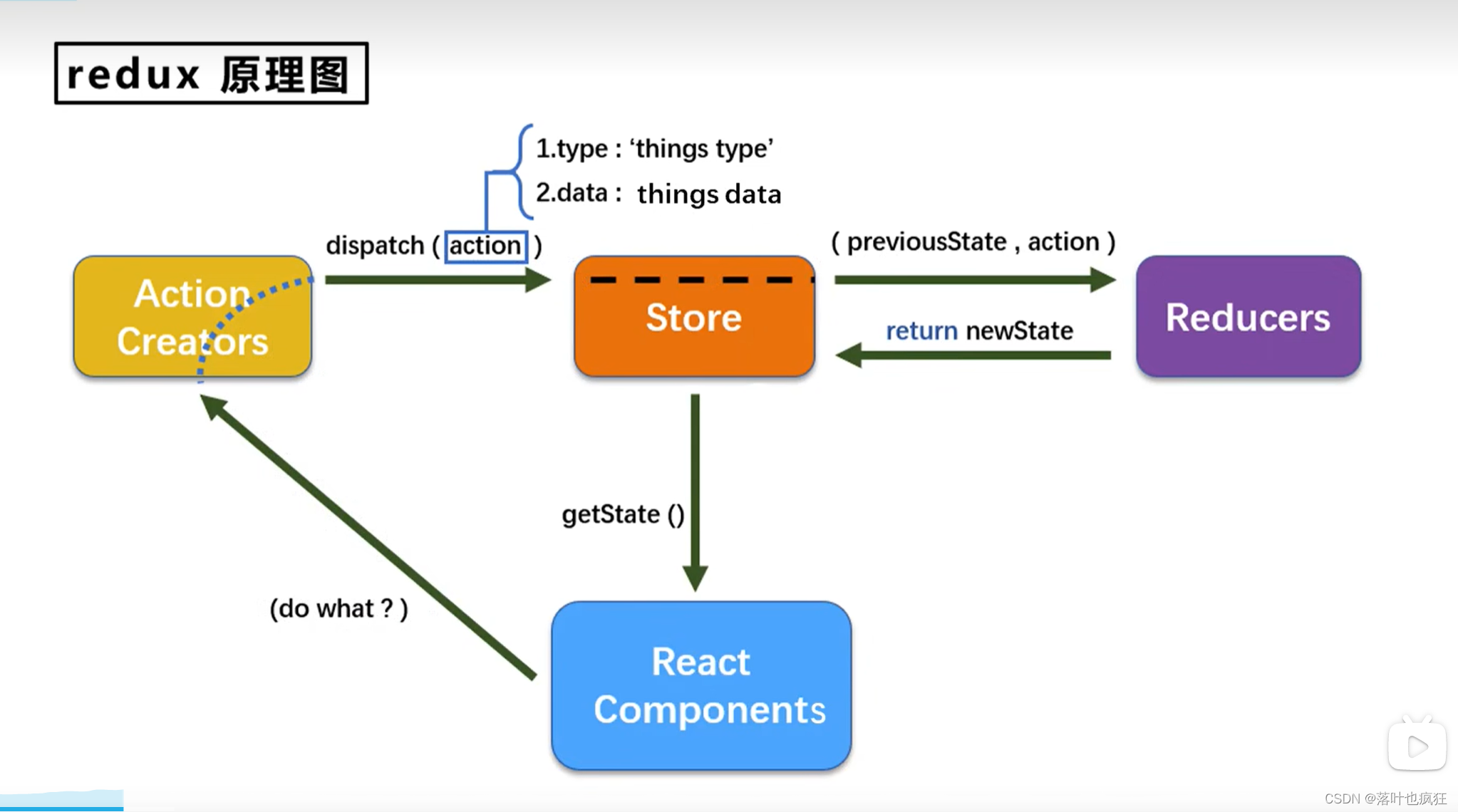
redux三大核心

Explain left value, right value, left value reference and right value reference in detail

使用WebMvcConfigurer进行接口请求拦截进行中增强(附源码)

The project parameters are made into configurable items, and the @configurationproperties annotation is used

IP第十四天笔记
![Shell中的文本处理工具、cut [选项参数] filename 说明:默认分隔符是制表符、awk [选项参数] ‘/pattern1/{action1}filename 、awk 的内置变量](/img/ed/941276a15d1c4ab67d397fb3286022.png)
Shell中的文本处理工具、cut [选项参数] filename 说明:默认分隔符是制表符、awk [选项参数] ‘/pattern1/{action1}filename 、awk 的内置变量
随机推荐
IIC 通信协议 (一)
数据库泰斗王珊:努力创新,精心打磨优质的数据库产品
Px4 module design 12: high resolution timer design
Is the e-commerce billing system important? How should the platform choose billing service providers?
els_ 画矩形、代码规划和备份
Shell中的文本处理工具、cut [选项参数] filename 说明:默认分隔符是制表符、awk [选项参数] ‘/pattern1/{action1}filename 、awk 的内置变量
【独立站建设】跨境电商出海开网店,首选这个网站建设!
Session&Cookie&token
Qstring conversion char*
els_ Rectangle drawing, code planning and backup
Deep analysis - dynamic memory management
Wechat applet editor Avatar
RSA asymmetric encryption and decryption signature verification tool
电商分账系统重要吗,平台应该如何选择分账服务商呢?
e.target与e.currentTarget的区别
STM32基于HAL库的串口接受中断和空闲中断
Chapter 6: cloud database
新手小白怎样开始学做自媒体呢?
利用JSON类型在mysql中实现数组功能
Overview of communication protocols