August 30, 2020: naked write algorithm: the nearest common ancestor of two nodes in a binary tree.

5 Line code , Can let wechat small program on the shelf to their own APP in | Register and send it to Dajiang 、 Huawei 、 Cherry keyboard ！>>>

Fogo's answer 2020-08-30：

1. recursive
Algorithm
Left node sub function return value is not empty , The return value of the sub function in the right node is null , Return to left node .
Left node sub function return value is null , The return value of the sub function in the right node is not empty , Back to the right node .
Left node sub function return value is not empty , The return value of the sub function in the right node is not empty , Returns the current node .
Complexity analysis ：
Time complexity O(N) ： among N Is the number of binary tree nodes ; In the worst case , You need to recursively traverse all the nodes of the tree .
Spatial complexity O(N) ： In the worst case , The depth of recursion reaches N , System use O(N) The size of the extra space .

2. Store the parent node
Ideas
We can use a hash table to store the parent nodes of all nodes , Then we can use the parent node information of the node from p The nodes start to jump up , And record the nodes that have been visited , Again from q The nodes start to jump up , If you encounter a node that has been visited , So this node is the nearest public ancestor we're looking for .
Algorithm
Traverse the whole binary tree from the root node , Use hash table to record the parent node pointer of each node .
from p The node begins to move towards its ancestors , And use the data structure to record the visited ancestor nodes .
Again , Let's go from q The node begins to move towards its ancestors , If any ancestors have been visited , That means it's p and q The deepest public ancestor , namely LCA node .
Complexity analysis
Time complexity ：O(N), among N It's the number of nodes in a binary tree . All nodes of the binary tree have and will only be accessed once , from p and q The number of ancestor nodes that the node jumps up will not exceed N, So the total time complexity is O(N).
Spatial complexity ：O(N), among N It's the number of nodes in a binary tree . The stack depth of recursive calls depends on the height of the binary tree , In the worst case, a binary tree is a chain , Now the height is N, So the space complexity is zero O(N), The hash table stores the parent node of each node, which also needs O(N) Spatial complexity of , So the final total space complexity is O(N).

3. iteration
Ideas
Depth-first traversal , Traverse to two values , The answer comes out .
Complexity analysis
Time complexity O(N) ： among N Is the number of binary tree nodes ; In the worst case , You need to recursively traverse all the nodes of the tree .
Spatial complexity O(Level) ： Level It's the maximum depth of the tree .

The code to use go Language writing , as follows ：

package test35_lowestcommonancestor

import (
    "fmt"
    "testing"
)

//go test -v -test.run TestLowestCommonAncestor
func TestLowestCommonAncestor(t *testing.T) {
    root := &TreeNode{}
    root.Val = 3

    root.Left = &TreeNode{}
    root.Left.Val = 5
    root.Right = &TreeNode{}
    root.Right.Val = 1

    root.Right.Left = &TreeNode{}
    root.Right.Left.Val = 0
    root.Right.Right = &TreeNode{}
    root.Right.Right.Val = 8

    root.Left.Left = &TreeNode{}
    root.Left.Left.Val = 6
    root.Left.Right = &TreeNode{}
    root.Left.Right.Val = 2

    root.Left.Right.Left = &TreeNode{}
    root.Left.Right.Left.Val = 7
    root.Left.Right.Right = &TreeNode{}
    root.Left.Right.Right.Val = 4
    p := root.Right.Right
    q := root.Left.Right.Right

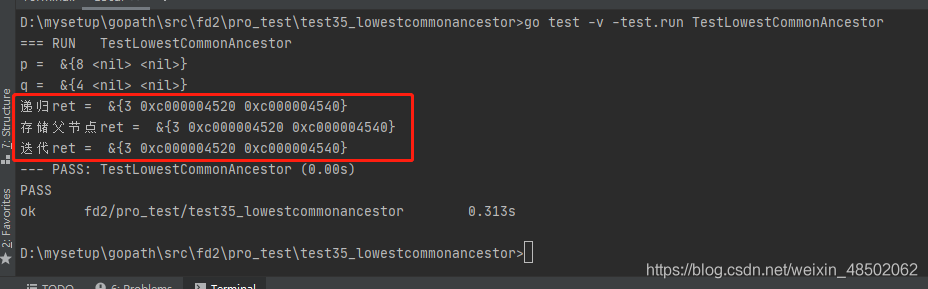
    fmt.Println("p = ", p)
    fmt.Println("q = ", q)
    ret := LowestCommonAncestor1(root, p, q)
    fmt.Println(" recursive ret = ", ret)
    ret = LowestCommonAncestor2(root, p, q)
    fmt.Println(" Store the parent node ret = ", ret)
    ret = LowestCommonAncestor3(root, p, q)
    fmt.Println(" iteration ret = ", ret)

}

//Definition for a binary tree node.
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

// recursive 
func LowestCommonAncestor1(root, p, q *TreeNode) *TreeNode {
    if root == nil || root == p || root == q {
        return root
    }
    left := LowestCommonAncestor1(root.Left, p, q)
    right := LowestCommonAncestor1(root.Right, p, q)
    if left == nil && right == nil { //root It's a leaf node 
        return nil
    }
    // The left node cannot be searched , The right node is the root node 
    if left == nil {
        return right
    }
    // The right node cannot be searched , The left node is the root node 
    if right == nil {
        return left
    }
    // There are... On the left and right , explain root It's the root node 
    return root
}

// Store the parent node 
func LowestCommonAncestor2(root, p, q *TreeNode) *TreeNode {
    parent := map[int]*TreeNode{}
    visited := map[int]bool{}

    var dfs func(*TreeNode)
    dfs = func(r *TreeNode) {
        if r == nil {
            return
        }
        if r.Left != nil {
            parent[r.Left.Val] = r
            dfs(r.Left)
        }
        if r.Right != nil {
            parent[r.Right.Val] = r
            dfs(r.Right)
        }
    }
    dfs(root)

    for p != nil {
        visited[p.Val] = true
        p = parent[p.Val]
    }
    for q != nil {
        if visited[q.Val] {
            return q
        }
        q = parent[q.Val]
    }

    return nil
}

// iteration 
func LowestCommonAncestor3(root, p, q *TreeNode) *TreeNode {
    if root == nil || root == p || root == q {
        return root
    }
    //push root 
    stack := make([]*TreeNode, 0)
    stack = append(stack, root)
    stackvisited := make([]int, 0)         // Record stack Access status of 
    stackvisited = append(stackvisited, 0) //0 Not accessed  1 The left node has accessed  2 The right node has accessed 

    var cur *TreeNode = nil
    var ret *TreeNode = nil
    for len(stack) > 0 {
        cur = nil
        if stackvisited[len(stackvisited)-1] == 0 { // Not accessed 
            stackvisited[len(stackvisited)-1] = 1
            if stack[len(stack)-1].Left != nil {
                stack = append(stack, stack[len(stack)-1].Left)
                stackvisited = append(stackvisited, 0)
                cur = stack[len(stack)-1]
            }
        } else if stackvisited[len(stackvisited)-1] == 1 { // Left node visited 
            stackvisited[len(stackvisited)-1] = 2
            if stack[len(stack)-1].Right != nil {
                stack = append(stack, stack[len(stack)-1].Right)
                stackvisited = append(stackvisited, 0)
                cur = stack[len(stack)-1]
            }
        } else { // The right node has accessed 
            if ret != nil {
                if stack[len(stack)-1] == ret {
                    ret = stack[len(stack)-2]
                }
            }
            //pop
            stack = stack[0 : len(stack)-1]
            stackvisited = stackvisited[0 : len(stackvisited)-1]
        }
        if cur != nil {
            if cur == p {
                if ret != nil { // The second time 
                    break
                } else { // for the first time 
                    ret = cur
                }
            }
            if cur == q {
                if ret != nil { // The second time 
                    break
                } else { // for the first time 
                    ret = cur
                }
            }
        }
    }

    return ret
}

knock go test -v -test.run TestLowestCommonAncestor command , The results are as follows ：

---

Comment on