2020-08-30：裸写算法：二叉树两个节点的最近公共祖先。

5行代码，即可让微信小程序上架到自己的APP中 | 注册送大疆、华为、樱桃键盘！>>>

福哥答案2020-08-30：

1.递归
算法
左节点子函数返回值不空，右节点子函数返回值为空，返回左节点。
左节点子函数返回值为空，右节点子函数返回值不空，返回右节点。
左节点子函数返回值不空，右节点子函数返回值不空，返回当前节点。
复杂度分析：
时间复杂度 O(N) ： 其中 N 为二叉树节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 O(N) ： 最差情况下，递归深度达到 N ，系统使用 O(N) 大小的额外空间。

2.存储父节点
思路
我们可以用哈希表存储所有节点的父节点，然后我们就可以利用节点的父节点信息从 p 结点开始不断往上跳，并记录已经访问过的节点，再从 q 节点开始不断往上跳，如果碰到已经访问过的节点，那么这个节点就是我们要找的最近公共祖先。
算法
从根节点开始遍历整棵二叉树，用哈希表记录每个节点的父节点指针。
从 p 节点开始不断往它的祖先移动，并用数据结构记录已经访问过的祖先节点。
同样，我们再从 q 节点开始不断往它的祖先移动，如果有祖先已经被访问过，即意味着这是 p 和 q 的深度最深的公共祖先，即 LCA 节点。
复杂度分析
时间复杂度：O(N)，其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次，从 p 和 q 节点往上跳经过的祖先节点个数不会超过 N，因此总的时间复杂度为 O(N)。
空间复杂度：O(N)，其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N，因此空间复杂度为 O(N)，哈希表存储每个节点的父节点也需要 O(N)的空间复杂度，因此最后总的空间复杂度为 O(N)。

3.迭代
思路
深度优先遍历，遍历到两个值，答案就出来了。
复杂度分析
时间复杂度 O(N) ： 其中 N 为二叉树节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 O(Level) ： Level是树的最大深度。

代码用go语言编写，如下：

package test35_lowestcommonancestor

import (
    "fmt"
    "testing"
)

//go test -v -test.run TestLowestCommonAncestor
func TestLowestCommonAncestor(t *testing.T) {
    root := &TreeNode{}
    root.Val = 3

    root.Left = &TreeNode{}
    root.Left.Val = 5
    root.Right = &TreeNode{}
    root.Right.Val = 1

    root.Right.Left = &TreeNode{}
    root.Right.Left.Val = 0
    root.Right.Right = &TreeNode{}
    root.Right.Right.Val = 8

    root.Left.Left = &TreeNode{}
    root.Left.Left.Val = 6
    root.Left.Right = &TreeNode{}
    root.Left.Right.Val = 2

    root.Left.Right.Left = &TreeNode{}
    root.Left.Right.Left.Val = 7
    root.Left.Right.Right = &TreeNode{}
    root.Left.Right.Right.Val = 4
    p := root.Right.Right
    q := root.Left.Right.Right

    fmt.Println("p = ", p)
    fmt.Println("q = ", q)
    ret := LowestCommonAncestor1(root, p, q)
    fmt.Println("递归ret = ", ret)
    ret = LowestCommonAncestor2(root, p, q)
    fmt.Println("存储父节点ret = ", ret)
    ret = LowestCommonAncestor3(root, p, q)
    fmt.Println("迭代ret = ", ret)

}

//Definition for a binary tree node.
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

//递归
func LowestCommonAncestor1(root, p, q *TreeNode) *TreeNode {
    if root == nil || root == p || root == q {
        return root
    }
    left := LowestCommonAncestor1(root.Left, p, q)
    right := LowestCommonAncestor1(root.Right, p, q)
    if left == nil && right == nil { //root是叶子节点
        return nil
    }
    //左节点搜索不到了，说明右节点是根节点
    if left == nil {
        return right
    }
    //右节点搜索不到了，说明左节点是根节点
    if right == nil {
        return left
    }
    //左右都有，说明root就是根节点
    return root
}

//存储父节点
func LowestCommonAncestor2(root, p, q *TreeNode) *TreeNode {
    parent := map[int]*TreeNode{}
    visited := map[int]bool{}

    var dfs func(*TreeNode)
    dfs = func(r *TreeNode) {
        if r == nil {
            return
        }
        if r.Left != nil {
            parent[r.Left.Val] = r
            dfs(r.Left)
        }
        if r.Right != nil {
            parent[r.Right.Val] = r
            dfs(r.Right)
        }
    }
    dfs(root)

    for p != nil {
        visited[p.Val] = true
        p = parent[p.Val]
    }
    for q != nil {
        if visited[q.Val] {
            return q
        }
        q = parent[q.Val]
    }

    return nil
}

//迭代
func LowestCommonAncestor3(root, p, q *TreeNode) *TreeNode {
    if root == nil || root == p || root == q {
        return root
    }
    //push根
    stack := make([]*TreeNode, 0)
    stack = append(stack, root)
    stackvisited := make([]int, 0)         //记录stack的访问状态
    stackvisited = append(stackvisited, 0) //0未访问 1左节点已经访问 2右节点已访问

    var cur *TreeNode = nil
    var ret *TreeNode = nil
    for len(stack) > 0 {
        cur = nil
        if stackvisited[len(stackvisited)-1] == 0 { //未访问
            stackvisited[len(stackvisited)-1] = 1
            if stack[len(stack)-1].Left != nil {
                stack = append(stack, stack[len(stack)-1].Left)
                stackvisited = append(stackvisited, 0)
                cur = stack[len(stack)-1]
            }
        } else if stackvisited[len(stackvisited)-1] == 1 { //左节点已访问
            stackvisited[len(stackvisited)-1] = 2
            if stack[len(stack)-1].Right != nil {
                stack = append(stack, stack[len(stack)-1].Right)
                stackvisited = append(stackvisited, 0)
                cur = stack[len(stack)-1]
            }
        } else { //右节点已访问
            if ret != nil {
                if stack[len(stack)-1] == ret {
                    ret = stack[len(stack)-2]
                }
            }
            //pop
            stack = stack[0 : len(stack)-1]
            stackvisited = stackvisited[0 : len(stackvisited)-1]
        }
        if cur != nil {
            if cur == p {
                if ret != nil { //第二次
                    break
                } else { //第一次
                    ret = cur
                }
            }
            if cur == q {
                if ret != nil { //第二次
                    break
                } else { //第一次
                    ret = cur
                }
            }
        }
    }

    return ret
}

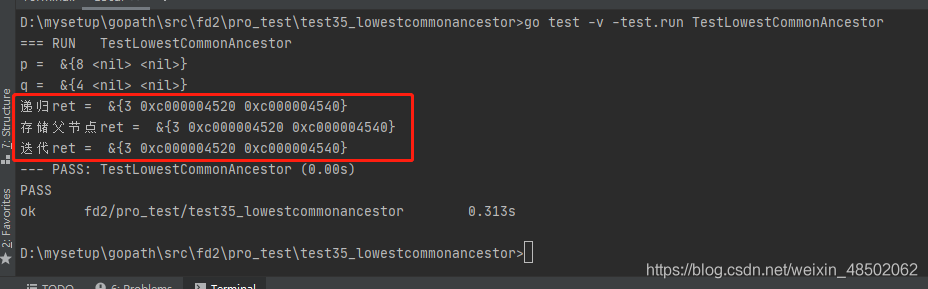
敲 go test -v -test.run TestLowestCommonAncestor 命令，执行结果如下：

---

评论