当前位置:网站首页>[combinatorics] recursive equation (four cases where the non-homogeneous part of a linear non-homogeneous recursive equation with constant coefficients is the general solution of the combination of po
[combinatorics] recursive equation (four cases where the non-homogeneous part of a linear non-homogeneous recursive equation with constant coefficients is the general solution of the combination of po
2022-07-03 17:24:00 【Programmer community】
List of articles
- One 、 Linear Nonhomogeneous recurrence equation with constant coefficients Of The nonhomogeneous part is polynomial And Index combination
- Two 、 Four cases of general solution of recurrence equation
One 、 Linear Nonhomogeneous recurrence equation with constant coefficients Of The nonhomogeneous part is polynomial And Index combination
If “ Linear Nonhomogeneous recurrence equation with constant coefficients ” Nonhomogeneous part of , yes
n
n
n Of
t
t
t Sub polynomial , And
β
n
\beta^n
βn The index of , The combination of ;
Then the form of its special solution , yes
n
n
n Of
t
t
t Sub polynomial , And
P
β
n
P\beta^n
Pβn Of and ;
Recurrence equation :
a
n
−
2
a
n
−
1
=
n
+
3
n
a_n - 2a_{n-1} = n + 3^n
an−2an−1=n+3n
initial value :
a
0
=
0
a_0 = 0
a0=0
General form ( important ) :
① The nonhomogeneous part is
n
n
n Of
t
t
t Sub polynomial :
- The characteristic root is not
1
1
1 , The special solution is
n
n
n Of
t
t
t Sub polynomial ;
- If the characteristic root is
1
1
1 , And the multiplicity is
e
e
e , So the special solution is
n
n
n Of
t
+
e
t + e
t+e Sub polynomial ;
② The nonhomogeneous part is
P
β
n
P\beta^n
Pβn :
- The characteristic root cannot be the bottom
β
\beta
β , The special solution is
P
β
n
P\beta^n
Pβn ;
- The characteristic root is the bottom
β
\beta
β , The multiplicity of the characteristic root is
e
e
e , The special solution is
P
n
e
β
n
Pn^e\beta^n
Pneβn ;
③ Homogeneous parts have no double roots :
H
(
n
)
=
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
H(n) = c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
H(n)=c1q1n+c2q2n+⋯+ckqkn
④ Homogeneous parts have double roots : General explanation
i
i
i term , Characteristic root
q
i
q_i
qi , Multiplicity
e
i
e_i
ei ,
H
i
(
n
)
=
(
c
i
1
+
c
i
2
n
+
⋯
+
c
i
e
i
n
e
i
−
1
)
q
i
n
H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n
Hi(n)=(ci1+ci2n+⋯+cieinei−1)qin , Final general solution
H
(
n
)
=
∑
i
=
1
t
H
i
(
n
)
H(n) = \sum\limits_{i=1}^tH_i(n)
H(n)=i=1∑tHi(n) ;
Reference blog : 【 Combinatorial mathematics 】 Recurrence equation ( Linear Nonhomogeneous recurrence equation with constant coefficients Of The nonhomogeneous part is polynomial And Index combination | Four cases of general solution )
Calculate the homogeneous partial general solution :
Homogeneous partial standard form of recurrence equation :
a
n
−
2
a
n
−
1
=
0
a_n - 2a_{n-1} = 0
an−2an−1=0
Characteristic equation :
x
−
2
=
0
x - 2 = 0
x−2=0
Characteristic root :
x
=
2
x=2
x=2
Homogeneous partial general solution :
a
n
‾
=
c
2
n
\overline{a_n} =c2^n
an=c2n
Calculate the non-homogeneous partial general solution :
The non-homogeneous part of the above recursive equation is
n
+
3
n
n + 3^n
n+3n , It consists of two parts :
n
n
n Of
t
t
t Sub polynomial :
n
n
n , The characteristic root is not
1
1
1, The corresponding special solution is
n
n
n Of
t
t
t Sub polynomial , In the form of
P
1
n
+
P
2
P_1n + P_2
P1n+P2 ;
β
n
\beta^n
βn Index :
3
n
3^n
3n , The characteristic root is not the bottom
3
3
3 , The corresponding special solution is
P
β
n
P\beta^n
Pβn form , In the form of
P
3
3
n
P_33^n
P33n ;
Complete special solution :
a
n
∗
=
P
1
n
+
P
2
+
P
3
3
n
a^*_n = P_1n + P_2 + P_33^n
an∗=P1n+P2+P33n
Put the special solution into the recursive equation :
(
P
1
n
+
P
2
+
P
3
3
n
)
−
2
[
P
1
(
n
−
1
)
+
P
2
+
P
3
3
n
−
1
]
=
n
+
3
n
(P_1n + P_2 + P_33^n) - 2[P_1(n-1) + P_2 + P_33^{n-1}] = n + 3^n
(P1n+P2+P33n)−2[P1(n−1)+P2+P33n−1]=n+3n
Expand the formula on the left :
−
P
1
n
+
(
2
P
1
−
P
2
)
+
P
3
3
n
−
1
=
n
+
3
n
-P_1n + (2P_1 - P_2) + P_33^{n-1}=n+3^n
−P1n+(2P1−P2)+P33n−1=n+3n
According to the analysis of
n
n
n The power of , Constant term ,
3
n
3^n
3n Correspondence of items , The following equations can be obtained :
{
−
P
1
=
1
2
P
1
−
P
2
=
0
P
3
3
=
1
\begin{cases} -P_1 = 1 \\\\ 2P_1 - P_2 = 0 \\\\ \cfrac{P_3}{3} =1 \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧−P1=12P1−P2=03P3=1
Solve the above equations , The result is :
{
P
1
=
−
1
P
2
=
−
2
P
3
=
3
\begin{cases} P_1 = -1 \\\\ P_2 = -2 \\\\ P_3 =3 \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧P1=−1P2=−2P3=3
Special solution : Substitute the above constant into
a
n
∗
=
P
1
n
+
P
2
+
P
3
3
n
a^*_n = P_1n + P_2 + P_33^n
an∗=P1n+P2+P33n in , Get the final special solution :
a
n
∗
=
−
n
−
2
+
3
n
+
1
a^*_n = -n - 2 + 3^{n+1}
an∗=−n−2+3n+1 ;
Homogeneous partial general solution form :
a
n
‾
=
c
2
n
\overline{a_n} =c2^n
an=c2n
Complete general solution :
a
n
=
a
n
‾
+
a
n
∗
=
c
2
n
−
n
−
2
+
3
n
+
1
a_n = \overline{a_n} + a^*_n = c2^n -n - 2 + 3^{n+1}
an=an+an∗=c2n−n−2+3n+1
Initial value
a
0
=
0
a_0 = 0
a0=0 Substitute the above general solution :
c
2
0
−
0
−
2
+
3
0
+
1
=
0
c2^0 - 0 - 2 + 3^{0+1} = 0
c20−0−2+30+1=0
c
−
2
+
3
=
0
c - 2 + 3 = 0
c−2+3=0
c
=
−
1
c=-1
c=−1
The general solution of the final recursive equation is
a
n
=
2
n
−
n
−
2
+
3
n
+
1
a_n = 2^n -n - 2 + 3^{n+1}
an=2n−n−2+3n+1
Two 、 Four cases of general solution of recurrence equation
General form ( important ) :
① The nonhomogeneous part is
n
n
n Of
t
t
t Sub polynomial :
- The characteristic root is not
1
1
1 , The special solution is
n
n
n Of
t
t
t Sub polynomial ;
- If the characteristic root is
1
1
1 , And the multiplicity is
e
e
e , So the special solution is
n
n
n Of
t
+
e
t + e
t+e Sub polynomial ;
② The nonhomogeneous part is
P
β
n
P\beta^n
Pβn :
- The characteristic root cannot be the bottom
β
\beta
β , The special solution is
P
β
n
P\beta^n
Pβn ;
- The characteristic root is the bottom
β
\beta
β , The multiplicity of the characteristic root is
e
e
e , The special solution is
P
n
e
β
n
Pn^e\beta^n
Pneβn ;
③ Homogeneous parts have no double roots :
H
(
n
)
=
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
H(n) = c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
H(n)=c1q1n+c2q2n+⋯+ckqkn
④ Homogeneous parts have double roots : General explanation
i
i
i term , Characteristic root
q
i
q_i
qi , Multiplicity
e
i
e_i
ei ,
H
i
(
n
)
=
(
c
i
1
+
c
i
2
n
+
⋯
+
c
i
e
i
n
e
i
−
1
)
q
i
n
H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n
Hi(n)=(ci1+ci2n+⋯+cieinei−1)qin , Final general solution
H
(
n
)
=
∑
i
=
1
t
H
i
(
n
)
H(n) = \sum\limits_{i=1}^tH_i(n)
H(n)=i=1∑tHi(n) ;
Reference blog : 【 Combinatorial mathematics 】 Recurrence equation ( Linear Nonhomogeneous recurrence equation with constant coefficients Of The nonhomogeneous part is polynomial And Index combination | Four cases of general solution )
边栏推荐
- One brush 148 force deduction hot question-5 longest palindrome substring (m)
- Is AI too slow to design pictures and draw illustrations? 3 sets of practical brushes to save you
- The difference between i++ and ++i: tell their differences easily
- Hongmeng third training
- [combinatorics] recursive equation (example of solving recursive equation without multiple roots | complete process of solving recursive equation without multiple roots)
- RDS数据库的监测页面在哪看?
- 【RT-Thread】nxp rt10xx 设备驱动框架之--rtc搭建和使用
- One brush 149 force deduction hot question-10 regular expression matching (H)
- Svn full backup svnadmin hotcopy
- Simple configuration of postfix server
猜你喜欢

Hongmeng third training
![[RT thread] NXP rt10xx device driver framework -- Audio construction and use](/img/85/32a83eaa4b7f5b30d4d7c4f4c32791.png)
[RT thread] NXP rt10xx device driver framework -- Audio construction and use

QT学习日记9——对话框
Collection of the most beautiful graduation photos in the graduation season, collection of excellent graduation photos
![[try to hack] active detection and concealment technology](/img/43/d48f851268fec566ce0cc83bd9557e.png)
[try to hack] active detection and concealment technology
![29: Chapter 3: develop Passport Service: 12: develop [obtain user account information, interface]; (use VO class to package the found data to meet the requirements of the interface for the returned da](/img/1c/c655c8232de1c56203873dcf171f45.png)
29: Chapter 3: develop Passport Service: 12: develop [obtain user account information, interface]; (use VO class to package the found data to meet the requirements of the interface for the returned da

Is AI too slow to design pictures and draw illustrations? 3 sets of practical brushes to save you
1164 Good in C
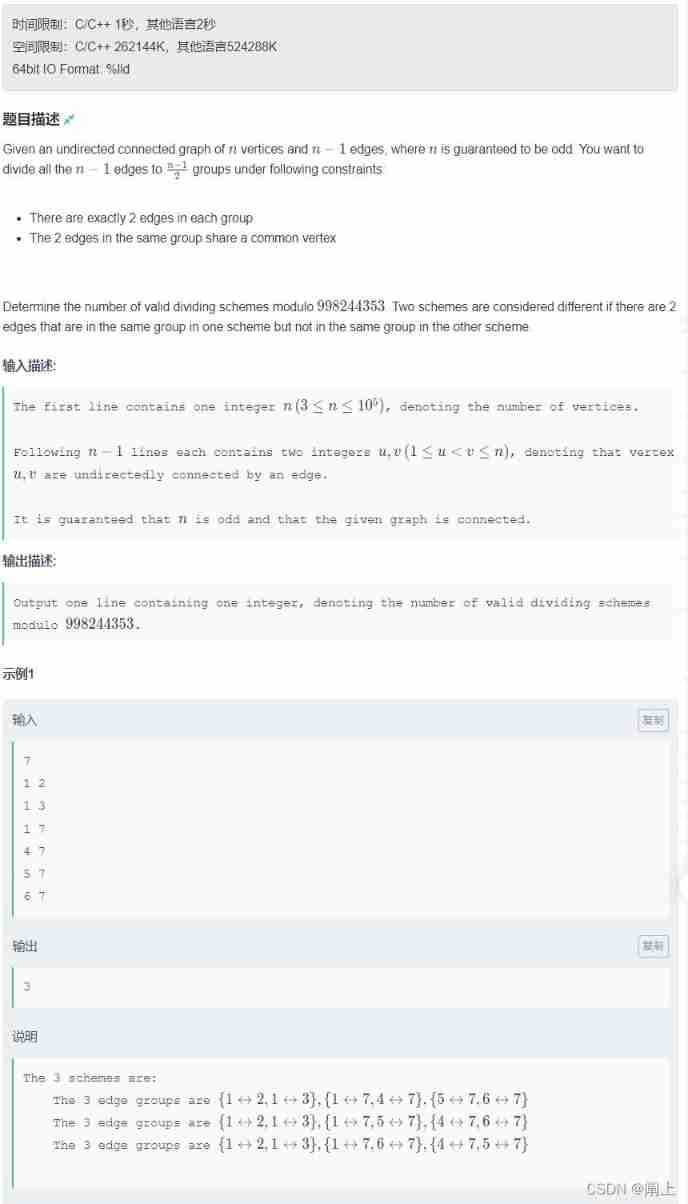
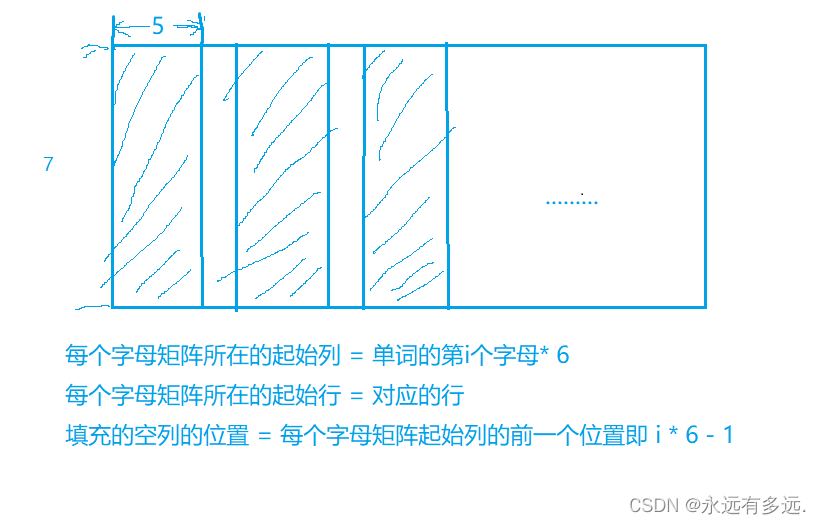
2021 ICPC regional competition (Shanghai) g.edge groups (tree DP)

Select 3 fcpx plug-ins. Come and see if you like them
随机推荐
[combinatorics] recursive equation (the problem of solving recursive equation with multiple roots | the problem is raised)
SVN完全备份svnadmin hotcopy
Is AI too slow to design pictures and draw illustrations? 3 sets of practical brushes to save you
Play with fancy special effects. This AE super kit is for you
绝对定位时元素水平垂直居中
The difference between i++ and ++i: tell their differences easily
SWM32系列教程4-端口映射及串口应用
Javescript variable declaration -- VaR, let, const
University of Electronic Science and technology, accounting computerization, spring 20 final exam [standard answer]
New library online | cnopendata China bird watching record data
One brush 144 force deduction hot question-1 sum of two numbers (E)
Define a structure fraction to represent a fraction, which is used to represent fractions such as 2/3 and 5/6
Simple use of unity pen XR grab
Apache服务挂起Asynchronous AcceptEx failed.
One brush 147-force deduction hot question-4 find the median of two positive arrays (H)
Squid service startup script
How to enforce parameters in PowerShell- How do I make parameters mandatory in PowerShell?
How SVN views modified file records
First day of rhcsa study
LeetCode13.罗马数字转整数(三种解法)