当前位置：网站首页>通俗理解时域采样与频域延拓

通俗理解时域采样与频域延拓

2022-06-12 08:41:00 【ZEERO~】

讲连续信号 $x_{a}(t)$ 与冲激串信号 $p_{s}(t)$ 相乘，即可得到离散时间信号 $x (n)$ ，因此，有如下公式：
$x(n)=x_{a}(t) |_{t=nT_{s}}=x_{a}(t)p_{s}(t)=x_{a}(t)\sum_{n=-\infty}^{\infty}\delta(t-nT_{s})$
采样周期为 $T_{s}$ ，我们用 $X_{a}(j\Omega)$ 来表示模拟信号 $x_{a}(t)$ 的频谱，用 $X(e^{jw})$ 来表示离散信号 $x (n)$ 的频谱，根据Fourier变换公式，
$X_{a}(j\Omega)=\int_{-\infty}^{\infty}x_{a}(t)e^{-j\Omega t}dt\\X(e^{jw})=\sum_{n=-\infty}^{\infty}x(n)e^{-jwn}$
示意图如下所示：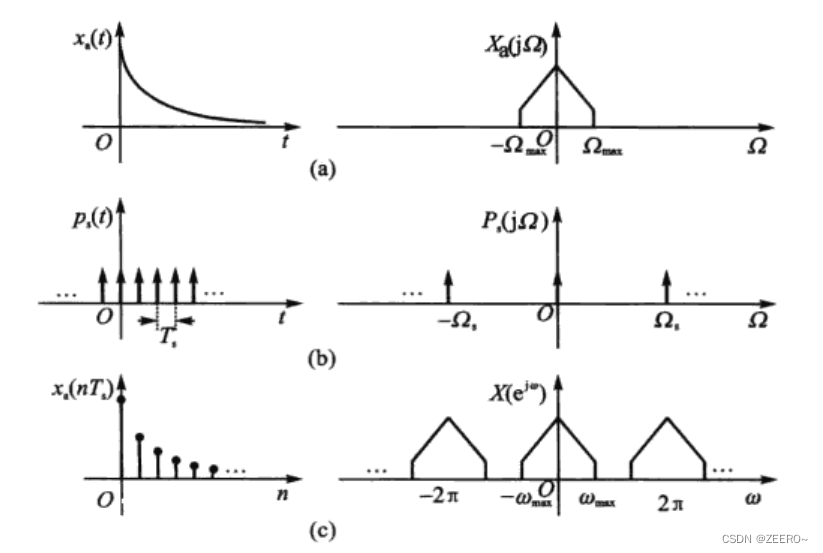
在这里插入图片描述
上图中，我们假设 $x_{a}(t)$ 为带限信号，就是频带有限长的信号，我们希望能找出 $X_{a}(j\Omega)$ 与 $X(e^{jw})$ 之间的区别和联系。
我们知道，离散信号可以视为一种特殊的连续信号，将其Fourier变换记为 $X_{s}(j\Omega)$ 。由模拟频率与数字频率的关系， $X_{s}(j\Omega)$ 与 $X(e^{jw})$ 之间的关系为
$X(e^{jw})=X_{s}(j\Omega) |_{\Omega =w/T_{s}}$
有关模拟频率和数字频率的关系，看这篇文章模拟频率与数字频率之间的关系。
我们接着往下讲，我们都知道，时域相乘等于频域的卷积，由数学公式表示
$X_{s}(j\Omega)=X_{a}(j\Omega)*P_{s}(j\Omega)$
，其中 $P_{s}(j\Omega)$ 为冲激信号串的Fourier变换。