当前位置:网站首页>MOOSE平台官方第二个例子分析——关于创建Kernel,求解对流扩散方程
MOOSE平台官方第二个例子分析——关于创建Kernel,求解对流扩散方程
2022-08-04 05:30:00 【nuomi666】
目录
内容可能存在错误,欢迎大家批评指正
一、例子介绍
本文使用的是官网上提供的第二例子( MOOSE|EX02),这个例子的求解的方程是在扩散方程(泊松方程)之上添加平流项,平流速度 v ⃗ \vec{v} v在 z z z方向上为 1 1 1,否则为零。其边界条件采用Dirichlet边界。在求解域底部上 u = 1 u=1 u=1 ,在顶部 u = 0 u=0 u=0 ,在剩余的其他边界上 ∇ u ⋅ n ^ = 0 \nabla u \cdot \hat{n} = 0 ∇u⋅n^=0,其中 n ^ \hat{n} n^是边界法向向量。
− ∇ ⋅ ∇ u + v ⃗ ⋅ ∇ u = 0 ∈ Ω u = 1 ∈ ∂ Ω b o t t o m u = 0 ∈ ∂ Ω t o p ∇ u ⋅ n ^ = 0 ∈ ∂ Ω o t h e r (1.1) \begin{aligned} -\nabla \cdot \nabla u + \vec{v} \cdot \nabla u&=0 && \quad \in \Omega \\ u &= 1 && \quad \in \partial \Omega_{bottom} \\ u &= 0 && \quad \in \partial \Omega_{top}\\ \nabla u \cdot \hat{n}& = 0 && \quad \in \partial \Omega_{other} \end{aligned} \tag{1.1} −∇⋅∇u+v⋅∇uuu∇u⋅n^=0=1=0=0∈Ω∈∂Ωbottom∈∂Ωtop∈∂Ωother(1.1)
二、FEM
1、生成弱形式
a.等式两侧同时乘测试函数 ψ \psi ψ
ψ ( − ∇ ⋅ ∇ u ) + ψ ( v ⃗ ⋅ ∇ u ) = 0 ψ , u ∈ V (2.1) \psi(-\nabla \cdot \nabla u) + \psi (\vec{v} \cdot \nabla u )=0 \quad \quad \psi,u \in V \tag{2.1} ψ(−∇⋅∇u)+ψ(v⋅∇u)=0ψ,u∈V(2.1)
这里 V = H 1 ( Ω ) V =H^{1}{(\Omega)} V=H1(Ω)
b.对整个求解域 Ω \Omega Ω积分
− ∫ Ω ψ ( ∇ ⋅ ∇ u ) + ∫ Ω ψ ( v ⃗ ⋅ ∇ u ) = 0 (2.2) -\int_{\Omega} \psi ( \nabla \cdot \nabla u)+\int_{\Omega}\psi(\vec{v} \cdot \nabla u ) =0 \tag{2.2} −∫Ωψ(∇⋅∇u)+∫Ωψ(v⋅∇u)=0(2.2)
c.分部积分
由于求导的性质有 ∇ ⋅ ( ψ ∇ u ) = ψ ∇ ⋅ ∇ u + ∇ ψ ⋅ ∇ u \nabla \cdot (\psi \nabla u)=\psi\nabla \cdot \nabla u+\nabla \psi \cdot \nabla u ∇⋅(ψ∇u)=ψ∇⋅∇u+∇ψ⋅∇u,带入(2.2)式左侧第一项得:
∫ Ω ∇ ψ ⋅ ∇ u − ∫ Ω ∇ ⋅ ( ψ ∇ u ) + ∫ Ω ψ ( v ⃗ ⋅ ∇ u ) = 0 (2.3) \int_{\Omega} \nabla \psi \cdot \nabla u-\int_{ \Omega}\nabla \cdot (\psi \nabla u)+\int_{\Omega} \psi(\vec{v} \cdot \nabla u )=0 \tag{2.3} ∫Ω∇ψ⋅∇u−∫Ω∇⋅(ψ∇u)+∫Ωψ(v⋅∇u)=0(2.3)
d.应用散度定理
散度定理可以理解成:考虑在流动得液体中取出体积为 V V V的部分,则流过该部分表面 S S S的液体通量等于散度在整个体积上的积分。
∭ V ( ∇ ⋅ F ) d V = ∯ s ( F ⋅ n ^ ) d S {\displaystyle \iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,\mathrm {d} V=} \oiint{\displaystyle \scriptstyle s}{\displaystyle (\mathbf {F} \cdot \mathbf {\hat {n}} )\,\mathrm {d} S} ∭V(∇⋅F)dV=∬s(F⋅n^)dS
左侧是在整个体积 V V V上的积分,右侧是在 V V V的表面边界 S S S上的积分, n ^ {\mathbf {\hat {n}} } n^是边界上外法线方向。
对(2.3)式的左侧第二项应用散度定理,(2.3)式可以写成
∫ Ω ∇ ψ ⋅ ∇ u − ∫ ∂ Ω ψ ( ∇ u ⋅ n ^ ) + ∫ Ω ψ ( v ⃗ ⋅ ∇ u ) = 0 ψ , u ∈ V (2.4) \int_{\Omega} \nabla \psi \cdot \nabla u-\int_{ \partial \Omega} \psi (\nabla u\cdot \mathbf {\hat {n}})+\int_{\Omega} \psi(\vec{v} \cdot \nabla u )=0 \quad \quad \psi,u \in V \tag{2.4} ∫Ω∇ψ⋅∇u−∫∂Ωψ(∇u⋅n^)+∫Ωψ(v⋅∇u)=0ψ,u∈V(2.4)
e.写成内积的形式
可以把(2.4)式用内积形式表示,其中每项都能在MOOSE中找到现有类进行继承
( ∇ ψ , ∇ u ) ⏟ K e r n e l − * ψ , ∇ u ⋅ n ^ * ⏟ B o u n d a r y C o n d i t i o n + ( ψ , v ⃗ ⋅ ∇ u ) ⏟ K e r n e l = 0 ψ , u ∈ V (2.5) \underbrace{\left(\nabla\psi, \nabla u \right)}_{Kernel} - \underbrace{\langle\psi, \nabla u\cdot \hat{n} \rangle}_{BoundaryCondition} + \underbrace{\left(\psi,\vec{v} \cdot \nabla u\right)}_{Kernel} = 0 \quad \quad \psi,u \in V \tag{2.5} Kernel(∇ψ,∇u)−BoundaryCondition*ψ,∇u⋅n^*+Kernel(ψ,v⋅∇u)=0ψ,u∈V(2.5)
2、等参单元
a ( ψ , u ) = ( ∇ ψ , ∇ u ) − * ψ , ∇ u ⋅ n ^ * + ( ψ , v ⃗ ⋅ ∇ u ) = ∫ Ω ∇ ψ ⋅ ∇ u − ∫ ∂ Ω ψ ( ∇ u ⋅ n ^ ) + ∫ Ω ψ ( v ⃗ ⋅ ∇ u ) = ∑ e ∣ J e ∣ [ ∫ Ω ^ e ∇ ψ i ⋅ ∇ u h − ∫ ∂ Ω ^ ψ i ( ∇ u h ⋅ n ^ ) + ∫ Ω ^ e ψ i ( v ⃗ ⋅ ∇ u h ) ] = 0 \begin{aligned} a(\psi,u)=&\left(\nabla\psi, \nabla u \right) - {\langle\psi, \nabla u\cdot \hat{n} \rangle} + \left(\psi,\vec{v} \cdot \nabla u\right)\\ =&\int_{\Omega} \nabla \psi \cdot \nabla u-\int_{ \partial \Omega} \psi (\nabla u\cdot \mathbf {\hat {n}})+\int_{\Omega} \psi(\vec{v} \cdot \nabla u )\\ =&\sum_e \left|\mathcal{J}_{e}\right| \left[\int_{\hat{\Omega}_e} \nabla \psi_i \cdot \nabla u_h-\int_{ \partial \hat{\Omega}} \psi_i (\nabla u_h\cdot \mathbf {\hat {n}})+\int_{\hat{\Omega}_e} \psi_i(\vec{v} \cdot \nabla u_h )\right]\\ =&0 \end{aligned} a(ψ,u)====(∇ψ,∇u)−*ψ,∇u⋅n^*+(ψ,v⋅∇u)∫Ω∇ψ⋅∇u−∫∂Ωψ(∇u⋅n^)+∫Ωψ(v⋅∇u)e∑∣Je∣[∫Ω^e∇ψi⋅∇uh−∫∂Ω^ψi(∇uh⋅n^)+∫Ω^eψi(v⋅∇uh)]0
其中
u ≈ u h = ∑ i n U i ψ i i = 1 , 2 , ⋯ n u \approx u_h=\sum_{i}^nU_{i}\psi_i \quad \quad i = 1,2,\cdots n u≈uh=i∑nUiψii=1,2,⋯n
这样刚度矩阵的
3、高斯积分
进行离散后的积分求解起来很麻烦,为了方便就采用了高斯积分的形式
∑ e ∫ Ω ^ e f ( ξ ˉ ) ∣ J e ∣ d ξ ˉ ≈ ∑ e ∑ q w q f ( x ˉ q ) ∣ J e ( x ˉ q ) ∣ \sum_{e} \int_{\hat{\Omega}_{e}} f(\bar{\xi})\left|\mathcal{J}_{e}\right| \mathrm{d} \bar{\xi} \approx \sum_{e} \sum_{q} w_{q} f\left(\bar{x}_{q}\right)\left|\mathcal{J}_{e}\left(\bar{x}_{q}\right)\right| e∑∫Ω^ef(ξˉ)∣Je∣dξˉ≈e∑q∑wqf(xˉq)∣Je(xˉq)∣
x ˉ q \bar{x}_{q} xˉq是正交点的位置, w q w_{q} wq是它的相关权重。
最终我们只需求解:
R ⃗ i ( u h ) = ∑ e ∑ q w q ∣ J e ∣ [ ∇ ψ i ⋅ ∇ u h + ψ i ( v ⃗ ⋅ ∇ u h ) ] ( x ⃗ q ) ⏟ Kernel Object(s) − ∑ f ∑ q f a c e w q f a c e ∣ J f ∣ [ ψ i ∇ u h ⋅ n ⃗ ] ( x ⃗ q f a c e ) ⏟ BoundaryCondition Object \begin{aligned} \vec{R}_i(u_h) &= \sum_e \sum_{q} w_{q} \left|\mathcal{J}_e\right|\underbrace{\left[ \nabla\psi_i\cdot \nabla u_h + \psi_i \left(\vec v \cdot \nabla u_h \right) \right](\vec{x}_{q})}_{\textrm{Kernel Object(s)}} \\ &- \sum_f \sum_{q_{face}} w_{q_{face}} \left|\mathcal{J}_f\right|\underbrace{\left[\psi_i \nabla u_h \cdot \vec{n} \right](\vec x_{q_{face}})}_{\textrm{BoundaryCondition Object}} \end{aligned} Ri(uh)=e∑q∑wq∣Je∣Kernel Object(s)[∇ψi⋅∇uh+ψi(v⋅∇uh)](xq)−f∑qface∑wqface∣Jf∣BoundaryCondition Object[ψi∇uh⋅n](xqface)
MOOSE平台关于高斯积分的介绍Quadrature,目前还没有太多说明。
三、输入文件
MOOSE会把输入文件和编译的app一块编译成而执行文件,然后运行输出,MOOSE的输入文件采用的是“分层输入文本”(hit)格式,基本的MOOSE输入文件包含六个部分
[Mesh]:定义求解的区域及剖分
[Variables]:定义需要求解的变量
[Kernels]:定义要解决的方程
[BCs]:定义边界条件
[Executioner]:定义解决问题的类型和方式
[Outputs]:定义结果如何输出
当然根据求解问题的需要也可以添加AuxVariables、AuxKernels、preconditioners、Postprocessors、Functions等更多的层。
[Kernels] #最外层名称不能随意更改,要使用MOOSE支持的层名
[Kernel_1] #内存名称可以用户自定义,方便阅读
type = Kernel_name #要用的物理模块,必须是编译的app包含在内的
variable = variable1 #该物理模块需要求解的变量名称
#根据Kernel的类型设置其他参数
[]
[Kernel_2] #需要多个物理模块,可以并列添加内部层
type = Kernel_name #同一个物理模块可以多次调用求解不同的变量
variable = variable2 #
[]
[] #内外层的开始和结尾都需要中括号
1、网格[mesh]
本例使用的网格是已经生成的ExodusII格式的网格文件,所以直接导入就行。共有3774个节点,2476个四边形剖分。
[Mesh]
file = mug.e
[]

MOOSE支持很多类型的网格文件导入,具体可以查看官网介绍(FileMesh)。
2、变量[Variables]
对于改问题要求解的方程
− ∇ ⋅ ∇ u + v ⃗ ⋅ ∇ = 0 -\nabla \cdot \nabla u + \vec{v} \cdot \nabla=0 −∇⋅∇u+v⋅∇=0
其中只包含一个变量 u u u。
[Variables]
[convected] #变量的名称
order = FIRST #基函数插值类型
family = LAGRANGE #阶数
[] #网格是QUAD4剖分,所以该变量采用拉格朗日一次插值
[]
3、物理模块[Kernels]
控制方程的弱形式除去边界边界项外还有两项:扩散项和对流项,所以物理模块应该选用两个。
[Kernels]
[diff]
type = Diffusion
variable = convected
[]
[conv]
type = ExampleConvection
variable = convected
velocity = '0.0 0.0 1.0'
[]
[]
物理模块由两个文件构成,存放在./include中的.h类型的头文件和存放在./src中.C类型的源文件
对于Diffusion模块,其头文件Diffusion.h
#pragma once //避免多次编译
#include "Kernel.h" //调用
class Diffusion : public Kernel //继承Kernel类
{
public:
//InputParameters:主要的MOOSE类负责处理几乎每个MOOSE系统中的用户定义参数。
static InputParameters validParams();
Diffusion(const InputParameters & parameters);//构造函数
protected:
virtual Real computeQpResidual() override;//残差求解函数,必须重载
virtual Real computeQpJacobian() override;//雅可比矩阵求解函数,必须重载
};
源文件Diffusion.C
#include "Diffusion.h"
//注册类名,通过这个将类编译进程序使用
registerMooseObject("MooseApp", Diffusion);
InputParameters
Diffusion::validParams() //构造Diffusion模块获取物理变量的函数
{
InputParameters params = Kernel::validParams();
//addClassDescription添加类描述
params.addClassDescription("The Laplacian operator ($-\\nabla \\cdot \\nabla u$), with the weak "
"form of $(\\nabla \\phi_i, \\nabla u_h)$.");
return params;
}
Diffusion::Diffusion(const InputParameters & parameters) : Kernel(parameters) {
}
Real
Diffusion::computeQpResidual()
{
return _grad_u[_qp] * _grad_test[_i][_qp];//继承的是Kernel,所以要使用_grad_test或_test
}
Real
Diffusion::computeQpJacobian()
{
return _grad_phi[_j][_qp] * _grad_test[_i][_qp];
}
平流项模块的头文件ExampleConvection.h
#pragma once
#include "Kernel.h"
class ExampleConvection : public Kernel
{
public:
/**这是构造函数的声明。 这个函数接受一个字符串和一个InputParameters对象, 就像其他Kernel-derived类。 */
ExampleConvection(const InputParameters & parameters);
/** validParams返回这个内核接受/需要的参数 */
static InputParameters validParams();
protected:
/** 计算一个积分点(节点)上的残差 */
virtual Real computeQpResidual() override;
/** * Responsible for computing the diagonal block of the preconditioning matrix. * This is essentially the partial derivative of the residual with respect to * the variable this kernel operates on ("u"). * * Note that this can be an approximation or linearization. In this case it's * not because the Jacobian of this operator is easy to calculate. * * This function should always be defined in the .C file. */
virtual Real computeQpJacobian() override;
private:
/** 用来储存向量,便于计算内积 */
RealVectorValue _velocity;
};
源文件ExampleConvection.C
#include "ExampleConvection.h"
//注册
registerMooseObject("ExampleApp", ExampleConvection);
//这个函数定义了这个内核的有效参数和它们的默认值
InputParameters
ExampleConvection::validParams()
{
InputParameters params = Kernel::validParams();
//这里使用了RealVectorValue所以velocity的传入值是向量
params.addRequiredParam<RealVectorValue>("velocity", "Velocity Vector");
return params;
}
ExampleConvection::ExampleConvection(const InputParameters & parameters)
: // 必须先调用基类的构造函数
Kernel(parameters),
_velocity(getParam<RealVectorValue>("velocity"))
{
}
Real
ExampleConvection::computeQpResidual()
{
// velocity * _grad_u[_qp] is actually doing a dot product
return _test[_i][_qp] * (_velocity * _grad_u[_qp]);
}
Real
ExampleConvection::computeQpJacobian()
{
// the partial derivative of _grad_u is just _grad_phi[_j]
return _test[_i][_qp] * (_velocity * _grad_phi[_j][_qp]);
}
4、边界条件[BCs]
[BCs]
[bottom]
type = DirichletBC
variable = convected
boundary = 'bottom'
value = 1
[]
[top]
type = DirichletBC
variable = convected
boundary = 'top'
value = 0
[]
[]
5、求解方式[Executioner]
[Executioner]
type = Steady #稳态,不含时间
solve_type = 'PJFNK' #带有预处理的JFNK
[]
6、输出[Outputs]
[Outputs]
execute_on = 'timestep_end' #时间结束执行该对象
exodus = true
[]
7、ex02_oversample.i
[Mesh]
type = GeneratedMesh #常用网格生成类
dim = 2 #网格维度是2
# x的最大坐标xmax为可选参数默认为1
# x的最小坐标xmin为可选参数默认为0
nx = 2 # x方向剖分的数目,默认为1
ny = 2 # y方向剖分的数目,默认为1
#这里选择的维度是2,所以不写nz,zmax应该也行,但是官网写了
nz = 0
zmax = 0 # z方向的最大坐标
elem_type = QUAD9 #网格剖分类型,默认是QUAD4,四个自由度的四边形网格
[]
[Variables]
[./diffused]
order = SECOND #网格9有个自由度,所以要采用二阶插值,默认是拉格朗日类型
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = diffused
[../]
[]
[DiracKernels]
[./foo]
variable = diffused #被施加负载的变量
type = ConstantPointSource #在网格中的单个位置施加负载
value = 1 # 负载
point = '0.3 0.3 0.0' #施加负载的位置
[../]
[]
[BCs]
[./all]
type = DirichletBC
variable = diffused
boundary = 'bottom left right top'
value = 0.0
[../]
[]
[Executioner]
type = Steady
solve_type = 'PJFNK'
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[./refine_2]
type = Exodus #输出文件类型
file_base = oversample_2 #输出文件名
refinements = 2
[../]
[./refine_4]
type = Exodus
file_base = oversample_4
#Number of uniform refinements for oversampling
#(refinement levels beyond any uniform refinements)
refinements = 4
[../]
[]
四、MOOSE常见代码
MOOSE的内核AD开头的是自动计算微分,如果选用AD类型,那么模型所用的所有模块都要调用AD开头的。
1、常见内置变量
_u,_grad_u 被操作变量的值和梯度。
_test,_grad_test 值( u u u)的测试函数 ψ \psi ψ 和梯度 ∇ ψ \nabla \psi ∇ψ
_i 测试功能组件的当前索引。
_q_point 当前节点的坐标。
_qp 当前节点索引。
2、InputParameters
“InputParameters”是一个C++类模板,声明和填充所有的参数,InputParameters 对象是一组参数,每个参数都有单独的属性,可用于精细控制底层对象的行为。例如,参数可以标记为必需或可选,提供或不提供默认值。输入参数的完整属性列表(InputParameters)。
每个类里包含的InputParameters都是使用静态方法validParams创建的,使用InputParameters方法创建一个名为Object的Kernel,其定义了两个参数,一个带有默认值1980的int类型的可选参数year和类型为int的必选参数month,以及相应的参数描述。
#include "Object.h"
//创建的所有基于MOOSE的对象类都必须使用这个宏把要创建的类在app内注册
//第一个参数是带有"App"后缀应用程序名称。
//第二个参数是创建的c++类的名称。
registerMooseObject("MOOSEApp", Object);
InputParameters
Object::validParams()
{
InputParameters params = Kernel::validParams(); //从父类开始
params.addParam<int>("year", 1980, "Provide the year you were born.")
params.addRequiredParam<int>("month", "Provide the month you were born.")
return params;
}
输入文件的Kernel层
[Kernel]
[date_object]
type = Object #使用已经在app内注册的Kernel
year = 2000 #此为选填参数,不填就用默认值1980
month = 6 #此为必选参数,不填程序报错
[]
[]
3、computeQpResidual
这个函数会出现在每个Kernel的末尾,用来计算残差。最好去看官网说明,说的比较清楚。
| 父类 | 覆盖 | 用法 |
|---|---|---|
| K e r n e l A D K e r n e l {\rm Kernel} \\ {\rm ADKernel} KernelADKernel | computeQpResidual | 当PDE中的项同时乘以测试函数和测试函数的梯度时使用(_test和_grad_test必须使用) |
| K e r n e l V a l u e A D K e r n e l V a l u e {\rm KernelValue} \\ {\rm ADKernelValue} KernelValueADKernelValue | precomputeQpResidual | 当PDE中计算的项仅乘以测试函数时使用(不用写_test参数,会自动应用) |
| K e r n e l G r a d A D K e r n e l G r a d {\rm KernelGrad} \\ {\rm ADKernelGrad} KernelGradADKernelGrad | precomputeQpResidual | 当PDE中计算的项仅乘以测试函数的梯度时使用(不用写_grad_test参数,会自动应用) |
使用实例对于弱形式:
( ∇ ψ , K μ ∇ p ) = 0 (\nabla \psi, \dfrac{K}{\mu} \nabla p) = 0 (∇ψ,μK∇p)=0
仅用到了测试函数的梯度,所以计算残差要继承KernelGrad或ADKernelGrad的precomputeQpResidual ,代码形式:
#pragma once
//调用ADKernelGrad基类
#include "ADKernelGrad.h"
//继承
class DarcyPressure : public ADKernelGrad
{
public:
static InputParameters validParams();
DarcyPressure(const InputParameters & parameters);
protected:
/// 静态函数,必须重载
virtual ADRealVectorValue precomputeQpResidual() override;
///变量的值
const Real _permeability;
const Real _viscosity;
};
//源文件计算残差,不用写_grad_test参数,会自动应用
ADRealVectorValue
DarcyPressure::precomputeQpResidual()
{
return (_permeability / _viscosity) * _grad_u[_qp];//这里的u就是求解变量p
}
4、
参考资料
[ 1 ] [1] [1]、Gockenbach M S . Understanding and Implementing the Finite Element Method[M]. Society for Industrial and Applied Mathematics, 2006.
[ 2 ] [2] [2]、https://mooseframework.inl.gov/
边栏推荐
- 图像形变(插值方法)
- 【CV-Learning】线性分类器(SVM基础)
- target has libraries with conflicting names: libcrypto.a and libssl.a.
- PP-LiteSeg
- The difference between oracle temporary table and pg temporary table
- Image-Adaptive YOLO for Object Detection in Adverse Weather Conditions
- MAE 论文《Masked Autoencoders Are Scalable Vision Learners》
- Linear Regression 02---Boston Housing Price Prediction
- [Deep Learning 21 Days Learning Challenge] Memo: What does our neural network model look like? - detailed explanation of model.summary()
- 双向LSTM
猜你喜欢
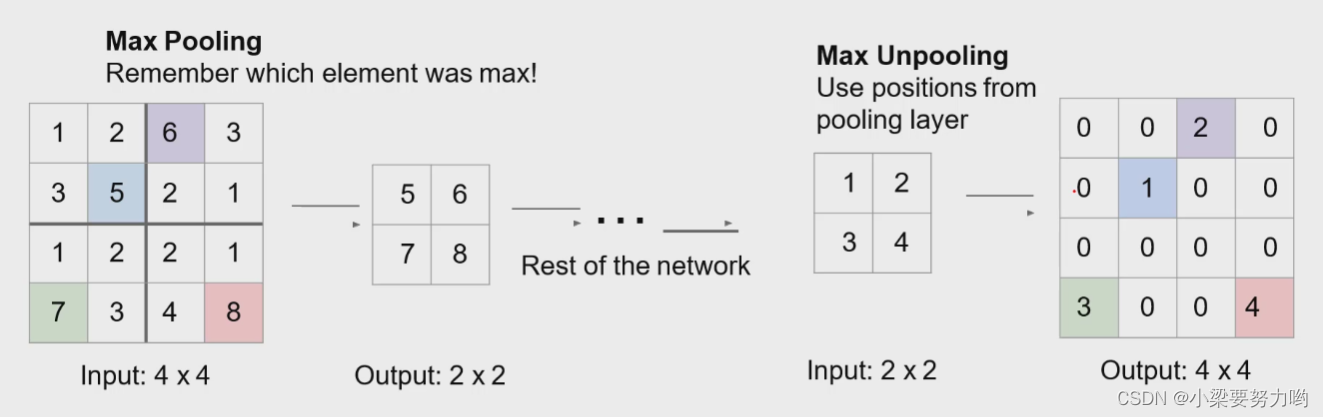
【CV-Learning】语义分割

【论文阅读】Mining Cross-Image Semantics for Weakly Supervised Semantic Segmentation
【深度学习日记】第一天:Hello world,Hello CNN MNIST
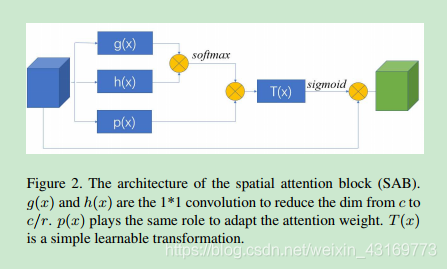
【论文阅读】Further Non-local and Channel Attention Networks for Vehicle Re-identification
Usage of RecyclerView

MFC读取点云,只能正常显示第一个,显示后面时报错

MAE 论文《Masked Autoencoders Are Scalable Vision Learners》

【CV-Learning】线性分类器(SVM基础)

Transformer
![[Go language entry notes] 13. Structure (struct)](/img/0e/44601d02a1c47726d26f0ae5085cc9.png)
[Go language entry notes] 13. Structure (struct)
随机推荐
简单说Q-Q图;stats.probplot(QQ图)
【CV-Learning】线性分类器(SVM基础)
Attention Is All You Need(Transformer)
Halcon缺陷检测
latex-写论文时一些常用设置
Polynomial Regression (PolynomialFeatures)
动手学深度学习_卷积神经网络CNN
TensorFlow2学习笔记:4、第一个神经网模型,鸢尾花分类
Usage of RecyclerView
属性动画的用法 以及ButterKnife的用法
TensorFlow2 study notes: 4. The first neural network model, iris classification
MySQL leftmost prefix principle [I understand hh]
Thoroughly understand box plot analysis
线性回归02---波士顿房价预测
Transformer
【Copy攻城狮日志】飞浆学院强化学习7日打卡营-学习笔记
sklearn中的学习曲线learning_curve函数
字典特征提取,文本特征提取。
[CV-Learning] Convolutional Neural Network Preliminary Knowledge
【CV-Learning】卷积神经网络