当前位置:网站首页>寻找第k小元素 前k小元素 select_k
寻找第k小元素 前k小元素 select_k
2022-07-05 17:43:00 【叮当的猫猫】
序言
不要offer的解决方法:先对所有元素排序,之后再找,这时时间复杂度在 O(nlgn)
快速选择算法 - Quick select
Quick select和Quick sort都是由Tony Hoare发明的
Quick select 的 平均时间复杂度为 O(n)
最差时间复杂度为 O(n^2)
算法没有使用额外空间,swap操作是inplace操作,所以空间复杂度为O(1)。

Quick select采用和Quick sort类似的步骤。首先选定一个pivot,然后根据每个数字与该pivot的大小关系将整个数组分为两部分。
那么与Quick sort不同的是,Quick select只考虑所寻找的目标所在的那一部分子数组,而非像Quick sort一样分别再对两边进行分割。正是因为如此,Quick select将平均时间复杂度从O(nlogn)降到了O(n)
public static int quickSelectK(int[] arr, int l, int r, int k) {
if (arr == null || arr.length == 0) {
return -1;
}
if (k > arr.length) return -1;
if (l == r) return arr[l];
int smallIndex = partitionForQuickSelect(arr, l, r);
int num = smallIndex - l + 1;
if (k == num) return arr[smallIndex];
else if (k < num) return quickSelectK(arr, l, smallIndex - 1, k);
else return quickSelectK(arr, smallIndex + 1, r, k - num);
}
private static int partitionForQuickSelect(int[] arr, int l, int r) {
int pivot = (int) (l + Math.random() * (r - l + 1));
swap(arr, pivot, r);
int less = l - 1;
for (int i = l; i < r; i++) {
if (arr[i] <= arr[r]) swap(arr, i, ++less);
}
swap(arr, less + 1, r);
return less + 1;
}
线性时间选择算法
期望为线性时间 - Randomized_Select 随机划分线性选择
输入数据是互异的。Randomized_Select算法以快速排序算法为模型,可以求一个数组中第k小的元素。
与快速排序不同的是,快速排序会递归处理划分的两边,而Randomized_Select只处理划分的一边
平均时间复杂度: O(n+k)=O(n) (当k比较小时)
由于划分操作 randomized_partition 的局限性,该选择算法的 最坏情况 时间复杂度 为 O(n^2)
快速排序算法需递归处理划分的两边,而选择算法则是只处理一边。
这一差异导致其性能上有所区别:
快速排序算法的期望运行时间为 Θ(nlgn),而选择算法的期望运行时间为 Θ(n)
核心:
每次以快排的枢纽划分数组 [ begin....mid...end ]
如果target<mid,则在 [ begin....mid-1 ]递归查找 第 k 个元素
如果target>mid,则在[ mid+1...end ]递归查找 第 k - (mid-begin+1) 个元素
public static int randomizedSelectK(int[] arr, int l, int r, int k) {
if (k > arr.length) return -1; //第 k 个 大于 数组长度
if (l == r) return arr[l]; //l == r 比如只有一个元素的数组,l==r
int lessIndex = randomizedPartition(arr, l, r);
int num = lessIndex - l + 1; //小于等于区最后一个下标 是当前 [l,r] 区域的第几个元素
if (num == k) {
//正好是第 k 个
return arr[lessIndex];
} else if (k < num) {
// 在小于等于区域,在 [l,lessIndex - 1] 区中找
return randomizedSelectK(arr, l, lessIndex - 1, k);
} else {
return randomizedSelectK(arr, lessIndex + 1, r, k - num); // 在大于区域,在 [lessIndex + 1,r] 区中找,注意最后的 k - num
}
}
//分区,找到 小于等于区的 最后一个下标
public static int randomizedPartition(int[] array, int l, int r) {
int pivot = (int) (l + Math.random() * (r - l + 1)); // 找一个 [l,r] 中的随机数
int lessIndex = l - 1; //l 的前一个元素
swap(array, pivot, r); //和最后一个元素交换
for (int i = l; i < r; i++) {
if (array[i] <= array[r]) {
//小于等于的话
swap(array, ++lessIndex, i); //和小于区域的后一个数交换 并自增
}
}
swap(array, lessIndex + 1, r); // 小于等于区的下一个数,和 r 交换,使得 lessIndex + 1 位置的数是小于等于区的最后一个数
return lessIndex + 1;
}
public static void main(String[] args) {
// int[] arr = {7, 1, 3, 4, 2, 6, 2, 8, 10, 9, 5};
int[] arr = {
30, 0, 61, 34, 69, 4, 75, 67, 23, 59, 16, 41, 33, 52, 3, 51, 23, 12, 28, 24, 12, 0, 44, 45, 14, 40, 28, 8, 4, 24, 2, 98, 32, 39, 73, 26, 2, 3, 1, 59, 82, 19, 4, 39, 33, 35, 6, 89, 70, 32, 16, 24, 24, 54, 13, 27, 25, 44, 79, 1, 38, 55, 49, 9, 6, 75, 86, 7, 20, 33, 46, 77, 35, 68, 9, 14, 2, 17, 12, 52, 13, 59, 88, 71, 6, 32, 28, 49, 11, 59, 66, 4, 16, 18, 6, 63, 17, 0};
for (int j = 1; j <= arr.length; j++) {
System.out.print(randomizedSelectK(arr, 0, arr.length - 1, j) + ", ");
}
System.out.println();
Arrays.sort(arr);
System.out.println(Arrays.toString(arr));
}
使用 分三个区域的 partition
快速选择算法 ( 数组中找第 K 大元素 ) - 分三个区
public static int randomizedSelectK(int[] arr, int l, int r, int k) {
if (k > arr.length) return -1;
if (l == r) return arr[l];
int[] p = randomizedPartition(arr, l, r); //分三个区
/** * 从等于区的第一个元素到 l 区第一个元素的个数,而不是从 小于区的最后一个到 l 的第一个元素 * 例如 * item 0 1 2 2 3 4 * index 0 1 2 3 4 5 * 假如 p = [2,3] * * k=2 时,res 应该为 1, 应该进入 if (k < lessPart) * k=3 时,res 应该为 2, 应该进入 if (k >= lessPart && k <= morePart) | 边界 lessPart = 3 = p[0] - l + d ==》 d = 1 * k=4 时,res 应该为 2, 应该进入 if (k >= lessPart && k <= morePart) | 边界 morePart = 4 = p[1] - l + c ==》 c = 1 * k=5 时,res 应该为 3, 应该进入 if (k > morePart) */
int lessPart = p[0] - l + 1;
int morePart = p[1] - l + 1;
if (k < lessPart) {
return randomizedSelectK(arr, l, p[0] - 1, k);
} else if (k > morePart) {
return randomizedSelectK(arr, p[1] + 1, r, k - morePart); //假设 k = 5, 那应该在 morePart 区域找第 1 个小的数,1 = 5 - 4 = k - morePart
} else {
return arr[p[0]]; //arr[p[0]] 或者 arr[p[1]]
}
}
public static int[] randomizedPartition(int[] arr, int l, int r) {
int rand = (int) (l + Math.random() * (r - l + 1));
swap(arr, rand, r);
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) swap(arr, ++less, l++);
else if (arr[l] > arr[r]) swap(arr, --more, l);
else l++;
}
swap(arr, more, r);
return new int[]{
less + 1, more};
}
最坏情况为线性时间 - SELECT 中位数线性时间选择
平均情况下能做到 O(N) 的复杂度
和 randomizedSelect 一样,select 算法通过对输入数组的递归划分来找出所需元素
但是,在划分的过程中 select 算法总能保证得到对数组的一个“好”的划分
select 使用的也是来自快速排序的确定性划分算法 partition ,但做了修改------把划分的主元也作为输入参数。
通过select算法,可确定一个有n>1个不同元素的输入数组中第p大的元素
以5个元素为1组 划分 集合
找出每组5个元素中的中位数
递归select算法找出这些中位数的中位数 k
上述过程时间复杂度本质为0(n)级别的
然后以k为枢纽运行Randomized Select算法的递归部分
由于k可以保证划分的最低下限(每个中位数保证有一半元素大于或小于它,所以中位数的中位数保证大于或小于的结点尽可能接近一半),故算法在最坏情况下也是0(n)级别的复杂度
第一步:分组
(1) 当规模小于某一阈值时,直接用排序算法返回结果。
(2) 当 n 大于 阈值 时,把 n 个元素划分为 n/5 分割的三个区间,若 n 不是5 的倍数,则排除剩余元素(不会有影响,这里只是为了求中项mm),最多只有1组由剩下的 n%5 个元素组成。
分别排序
然后挑出 每一组元素的中间值
再对 所有的中间值 ,递归调用 本算法,挑出中间值 mm,mm 即为 中项的中项
(3) 将所有元素划分为 A1、A2、A3 三组,分别包含 小于、等于、大于 mm 的元素
第二步:判断 k 在 哪一组
分三种情况,求出 第 k 小元素在这三个数组中的哪一个:
a.若 A1 的元素数量 大于等于k ,即 第K个元素在 A1组 内:在 A1 中 递归查找 第k小元素
p<k ,则在低区递归调用select查找第k大的元素
b.若 A1 的元素数量 小于 k ,并且 A1 和 A2 元素个数 之和大于等于 k,即 第k个元素 在 A2 中,A2 中 元素都是 mm:返回mm
p=k (p是 partition 返回值,k是要选择的第k大的元素),则返回 a[p] //下面代码是按照这里
c.否则,第k个元素在 A3组:在 A3 中 递归寻找第(k-|A1、A2元素数量之和|)小元素
若 p>k ,则在高区递归调用select查找第 p-k 大的元素


public static int select(int[] arr, int l, int r, int k) {
if (r - l < 75) {
quickSort(arr, l, r); //用插入排序进行排序
return arr[l + k - 1];
}
//分组
int group = (r - l + 5) / 5; //每组 5 个数 共 group 组
for (int i = 0; i < group; i++) {
int left = l + 5 * i;
int right = (l + i * 5 + 4) > r ? r : l + i * 5 + 4; //如果超出右边界就用右边界赋值
int mid = (left + right) / 2;
quickSort(arr, left, right); //每组进行 排序
swap(arr, l + i, mid); // 将各组中位数与 第 i 个 交换
}
int pivot = select(arr, l, l + group - 1, (group + 1) / 2); //找出中位数的中位数
int p = partition(arr, l, r, pivot); //用中位数的中位数作为基准的位置
int leftNum = p - l + 1; //leftNum 用来记录 基准位置前边 的元素个数
if (k == leftNum)
return arr[p];
else if (k < leftNum)
return select(arr, l, p - 1, k);
else //若k在基准位子的后边,则要从基准位置的后边数起,即第(k - leftNum - 1)个
return select(arr, p + 1, r, k - leftNum - 1);
}
private static int partition(int[] array, int start, int end, int pivot) {
int smallIndex = start - 1;
swap(array, pivot, end);
for (int i = start; i <= end; i++)
if (array[i] <= array[end]) {
smallIndex++;
if (i > smallIndex)
swap(array, i, smallIndex);
}
return smallIndex;
}
边栏推荐
- Short the command line via jar manifest or via a classpath file and rerun
- [BeanShell] there are many ways to write data locally
- Size_ T is unsigned
- Cartoon: interesting pirate problem (full version)
- 职场进阶指南:大厂人必看书籍推荐
- LeetCode 练习——206. 反转链表
- 服务器配置 jupyter环境
- 论文阅读_中文NLP_LTP
- How to modify MySQL fields as self growing fields
- Cartoon: interesting [pirate] question
猜你喜欢

PMP认证需具备哪些条件啊?费用多少啊?
「运维有小邓」用于云应用程序的单点登录解决方案

leetcode每日一练:旋转数组

7 pratiques devops pour améliorer la performance des applications
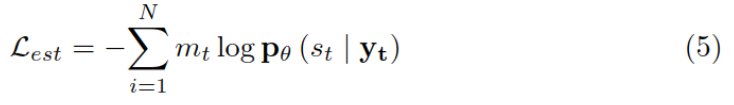
Thesis reading_ Medical NLP model_ EMBERT
神经网络自我认知模型

“12306” 的架构到底有多牛逼?
Compter le temps d'exécution du programme PHP et définir le temps d'exécution maximum de PHP
Short the command line via jar manifest or via a classpath file and rerun

Abnormal recovery of virtual machine Oracle -- Xi Fenfei
随机推荐
Read libco save and restore the on-site assembly code
Cmake tutorial Step3 (requirements for adding libraries)
7 pratiques devops pour améliorer la performance des applications
提高应用程序性能的7个DevOps实践
Please tell me why some tables can find data by writing SQL, but they can't be found in the data map, and the table structure can't be found
leetcode每日一题:字符串中的第一个唯一字符
GFS分布式文件系统
论文阅读_医疗NLP模型_ EMBERT
Compared with the loss of Wenxin, the performance is improved a lot
Customize the theme of matrix (I) night mode
请问下为啥有的表写sql能查到数据,但在数据地图里查不到啊,查表结构也搜不到
Six bad safety habits in the development of enterprise digitalization, each of which is very dangerous!
Server configuration jupyter environment
毫无章法系列
PMP认证需具备哪些条件啊?费用多少啊?
Cartoon: looking for the k-th element of an unordered array (Revised)
Leetcode exercise - 206 Reverse linked list
Redis基础
Delete some elements in the array
Sentinel-流量防卫兵